自顶向下递归实现(Recursive top-down implementation)
程序CUT-ROD对等式(14.2)进行了实现，伪代码如下：

CUT-ROD(p, n)
    if n == 0
        return 0
    q = -∞
    for i = 1 to n
        q = max{q, p[i] + CUT-ROD(p, n - i)}
    return q

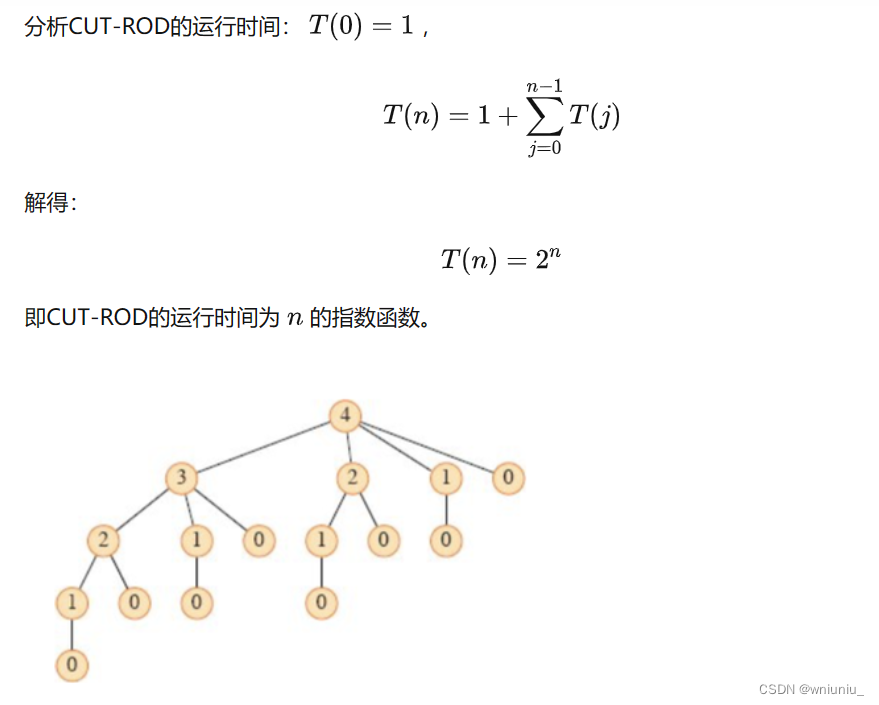
上面解决中重复对一个子结构问题重复求解了，我们可以把这个过程记录下来

使用动态规划求解最优钢条切割(Using dynamic programming for optimal rod cutting)

MEMOIZED-CUT-ROD(p, n)
    let r[0 : n] be a new array    // will remember solution values in r
    for i = 0 to n
        r[i] = -∞
    return MEMOIZED-CUT-ROD-AUX(p, n, r)

MEMOIZED-CUT-ROD-AUX(p, n, r)
    if r[n] ≥ 0    // already have a solution for length n ?
        return r[n]
    if n == 0
        q = 0
    else q = -∞
        for i = 1 to n    // i is the position of the first cut
            q = max{q, p[i] + MEMOIZED-CUT-ROD-AUX(p, n - i, r)}
    r[n] = q    // remember the solution value for length n
    return q

代码

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>

class Solution {
public:
	Solution(int x):len(x)
	{

	}

	int fun() {
		for (int i = 0; i <= len; i++) {
			memory[i] = 0;  // 初始化
		}
		for (int i = 1; i <= len; i++)
		{
			int q = min;
			for (int k = 1; k <= i; k++)
			{
				q =std::max( q , price[k] + memory[i - k]);   // 每次切割一次，这是核心
				record[i] = k;
			}
			memory[i] = q;
		}
		return memory[len];
	}

private:
	int price[11] = {0,1,5,8,9,10,17,17,20,24,30};  // 假定数据较小,对应价格
	int len;
	int memory[11];   // 记录 
	int record[11];   // 在哪里切割
	int min = -1;
};

int main()
{
	Solution a(4);
	std::cout <<a.fun() << std::endl;
}