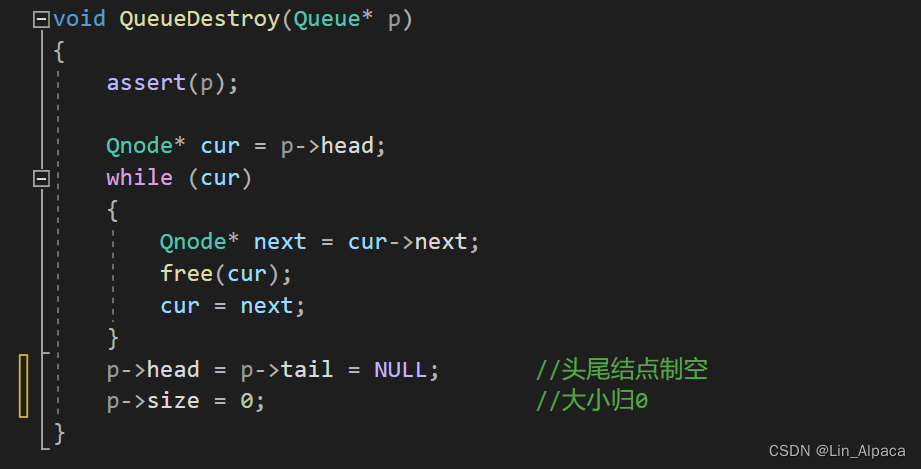
有两种形状的瓷砖:一种是 2 x 1 的多米诺形,另一种是形如 “L” 的托米诺形。两种形状都可以旋转。
给定整数 n ,返回可以平铺 2 x n 的面板的方法的数量。返回对 10^9 + 7 取模 的值。
平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同,当且仅当面板上有四个方向上的相邻单元中的两个,使得恰好有一个平铺有一个瓷砖占据两个正方形。
示例
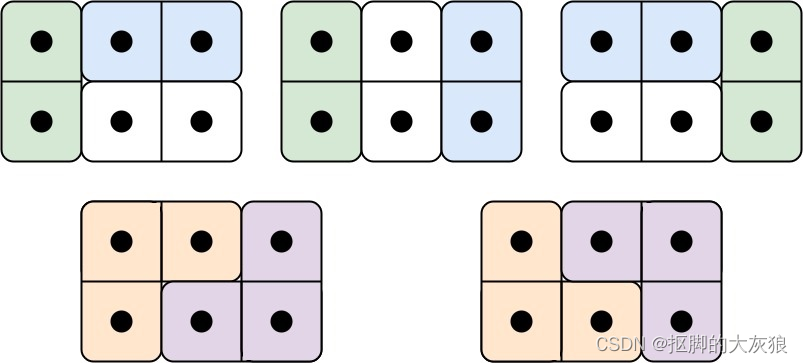
输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。
状态表示
我们从左到右依次扫描每一列,并维护当前列的状态。
这样来定义状态数组:
设dp[i][s]表示,前i列已经全部填满,且第i + 1列的填充状态为s时的总方案数。
比如,容易得知,dp[0][0] = 1。什么意思呢?就是把第0列全部填满,且第1列的填充状态为0(一个方块也没有被填充),这种状态可以通过在第0列竖着插入一个2 × 1的多米诺形达到,所以其方案数为1,如下图
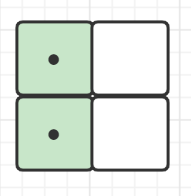
我们继续,看一下在第0列被填满,第1列的状态还可能是哪些呢?比较明显,还有下面3种情况:
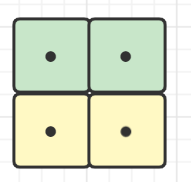


这三种情况对应的状态分别是
dp[0][3](3的二进制表示是11,表示第1列的2个方块都被填充了)
dp[0][2](2的二进制表示是10,高位的1表示第1列最顶部的方块被填充了)
dp[0][1](1的二进制表示是01,低位的1表示第1列最底部的方块被填充了)
这4种状态就是我们动态规划的边界条件,或者初始状态。
所以我们的初始状态有:dp[0][0] = dp[0][1] = dp[0][2] = dp[0][3] = 1。
接下来看看最终答案是什么。很明显,最终答案应当是,将前n - 1列全部填满,且第n列的填充状态为0时的总方案数,即dp[n - 1][0]。
状态转移
然后来看状态转移。
我们初始时先把第0列填满了,所以我们从第1列开始填充,即i从1开始循环。
每次枚举,前i - 1列都全部填满时,第i列的状态 (一共只有4种状态) ,然后看看当第i列处于某种状态时,我们可以如何把第i列填满。
- 前
i - 1列都填满,且第i列的状态为00时(dp[i - 1][0])
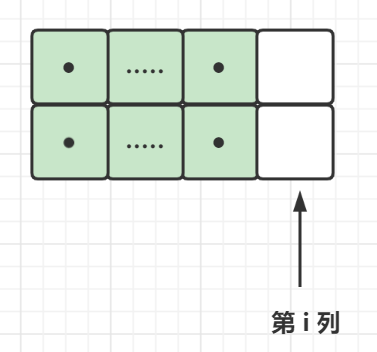
此时,对于第i列,我们可以
- 竖着插入一个
2 × 1的多米诺,此时能得到这样的状态:前i列都填满了,且第i + 1列的状态为00(dp[i][0]) - 横着插入2个
2 × 1的多米诺,此时第i + 1列的状态为11(dp[i][3]) - 插入1个
L形的托米诺,由于这个L形的托米诺能够旋转,所以能得到两种i + 1列的状态:01和10(dp[i][1]和dp[i][2])
所以,由dp[i - 1][0],能够转换到dp[i][0],dp[i][3],dp[i][1],dp[i][2]。也就是说dp[i - 1][0]对dp[i][0~3]全部4种状态都有贡献,所以转换到dp[i][0~3]这4种状态时,都要加上dp[i - 1][0]。
- 前
i - 1列都填满,且第i列的状态为01时(dp[i - 1][1])
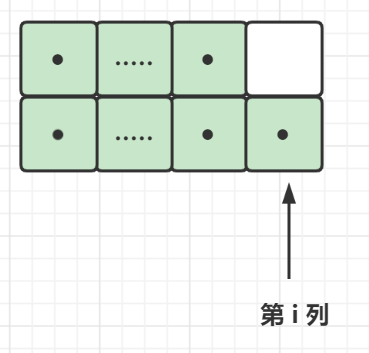
此时,对于第i列,我们可以
- 横着插入一个
2 × 1的多米诺,第i + 1列的状态为10(dp[i][2]) - 插入一个
L形的托米诺,第i + 1列的状态为11(dp[i][3])
所以,由dp[i - 1][1],能够转换到dp[i][2],dp[i][3]
- 前
i - 1列都填满,且第i列状态为10时(dp[i - 1][2])
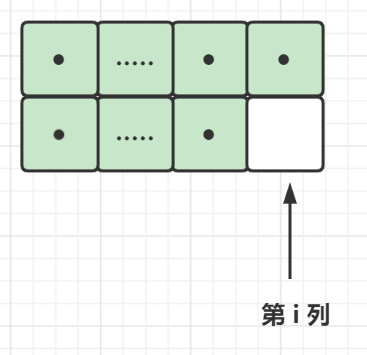
此时,对于第i列,我们可以
- 横着插入一个
2 × 1的多米诺,第i + 1列的状态为01(dp[i][1]) - 插入一个
L形的托米诺,第i + 1列的状态为11(dp[i][3])
所以,由dp[i - 1][2],能够转换到dp[i][1],dp[i][3]
- 前
i - 1列都填满,且第i列状态为11时(dp[i - 1][3])
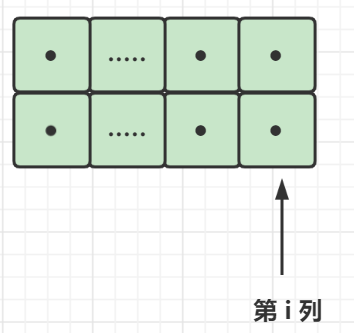
此时,对于第i列,我们无法再插入任何方块。只能得到第i + 1列的状态为00(dp[i][0])
所以,由dp[i - 1][3],能够转换到dp[i][0]
我们将上面,dp[i - 1][0~3]与dp[i][0~3]的关系,进行一下整理,容易得到状态转移方程如下
dp[i][0] = dp[i - 1][0] + dp[i - 1][3]dp[i][1] = dp[i - 1][0] + dp[i - 1][2]dp[i][2] = dp[i - 1][0] + dp[i - 1][1]dp[i][3] = dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][2]
代码
于是就能写出如下代码
typedef long long LL;
const int MOD = 1e9 + 7;
class Solution {
public:
int numTilings(int n) {
vector<vector<LL>> dp(n, vector<LL>(4, 0));
// dp[i][s]表示前i列已经填好, 伸出去第i + 1列情况为 s 时的方案数
dp[0][0] = dp[0][1] = dp[0][2] = dp[0][3] = 1;
for (int i = 1; i < n; i++) {
dp[i][0] = (dp[i - 1][0] + dp[i - 1][3]) % MOD;
dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % MOD;
dp[i][2] = (dp[i - 1][0] + dp[i - 1][1]) % MOD;
dp[i][3] = (dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][2]) % MOD;
}
// 答案返回前n - 1列已经全部填好, 且伸出去第i + 1列情况为0时的方案数
return (int) dp[n - 1][0];
}
};
并且由于dp[i][0~3]只依赖于dp[i - 1][0~3],还能用滚动数组进行优化
typedef long long LL;
const int MOD = 1e9 + 7;
class Solution {
public:
int numTilings(int n) {
LL s0, s1, s2, s3;
s0 = s1 = s2 = s3 = 1;
for (int i = 1; i < n; i++) {
LL t0 = (s0 + s3) % MOD;
LL t1 = (s0 + s2) % MOD;
LL t2 = (s0 + s1) % MOD;
LL t3 = (s0 + s1 + s2) % MOD;
s0 = t0;
s1 = t1;
s2 = t2;
s3 = t3;
}
return (int) s0;
}
};
PS: 这些都是俺从y总那里学到的(●’◡’●)
y总牛逼!(❤ ω ❤)