在 SocketCAN 中,can_bittiming_const 结构体用于表示 CAN 总线的定时参数,包括位率(bitrate)的计算。can_bittiming_const 包含了许多与位率相关的参数,其中一些参数用于计算实际的位率。
下面是一些与位率计算相关的字段:
-
brp(Baud Rate Prescaler):这是一个分频因子,用于确定位时间。brp的值由can_bittiming_const结构体的成员brp_min和brp_max决定。 -
prop_seg(Propagation Segment):传播时间段,表示信号在网络上传播的时间。 -
phase_seg1(Phase Buffer Segment 1):相位缓冲段 1,表示位时间的第一个时间段。 -
phase_seg2(Phase Buffer Segment 2):相位缓冲段 2,表示位时间的第二个时间段。 -
sjw(Synchronization Jump Width):同步跳变宽度,用于同步。
在 SocketCAN 中,实际的位率(bitrate)可以通过以下公式计算:
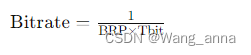
其中,
Tbit=Propagation Segment+Phase Buffer Segment 1+Phase Buffer Segment 2Tbit=Propagation Segment+Phase Buffer Segment 1+Phase Buffer Segment 2
这里是一个简化的例子,演示了如何使用 can_bittiming_const 结构体计算位率:
#include <linux/can.h>
void calculate_bitrate(const struct can_bittiming_const *btc) {
double Tbit = btc->prop_seg + btc->phase_seg1 + btc->phase_seg2;
double bitrate = 1.0 / (btc->brp * Tbit);
printf("Bitrate: %f bps\n", bitrate);
}
int main() {
struct can_bittiming_const btc;
// 初始化 btc 结构体的各个字段
// ...
calculate_bitrate(&btc);
return 0;
}
在实际使用中,你需要根据 CAN 控制器和网络的具体参数来初始化 can_bittiming_const 结构体,然后使用上述公式计算位率。
因为SocketCAN driver自身架构的原因,我们的driver并不会直接计算通讯速率相关的参数,而是由协议层根据我们driver提供的相关参数(时钟频率,TSEG 最大最小值等)的信息,以及APP 需要的baudrate,计算出最终的通讯参数(BRP,TSEG1,TSEG2,SJW)并设置这些标准通讯参数到driver。因此我们无法在driver层进行速率校验,因为driver看到的就不是baudrate,而是BRP,TSEG1,TSEG2,SJW 这些参数。
另外,如果简单的从上面的原因分析,貌似我们可以通过调整driver 提供给协议层的相关参数常量的最大/最小值来达成baudrate的限制。是的,我们确实可以通过这种方式来限制baudrate的最大值,但是当我们仔细研究了CAN 协议层关于通讯参数的算法后会发现这种方法得不偿失,它会导致在一些通讯频率上误差偏大。
CAN 协议层通讯参数计算的算法请参考:
calc_bittiming.c - drivers/net/can/dev/calc_bittiming.c - Linux source code (v6.6.2) - Bootlin