【学习草稿】pid控制基础实现--往水桶注水

news2024/11/15 4:23:35

pid

1）非常通俗易懂的PID控制（1）https://zhuanlan.zhihu.com/p/37515841
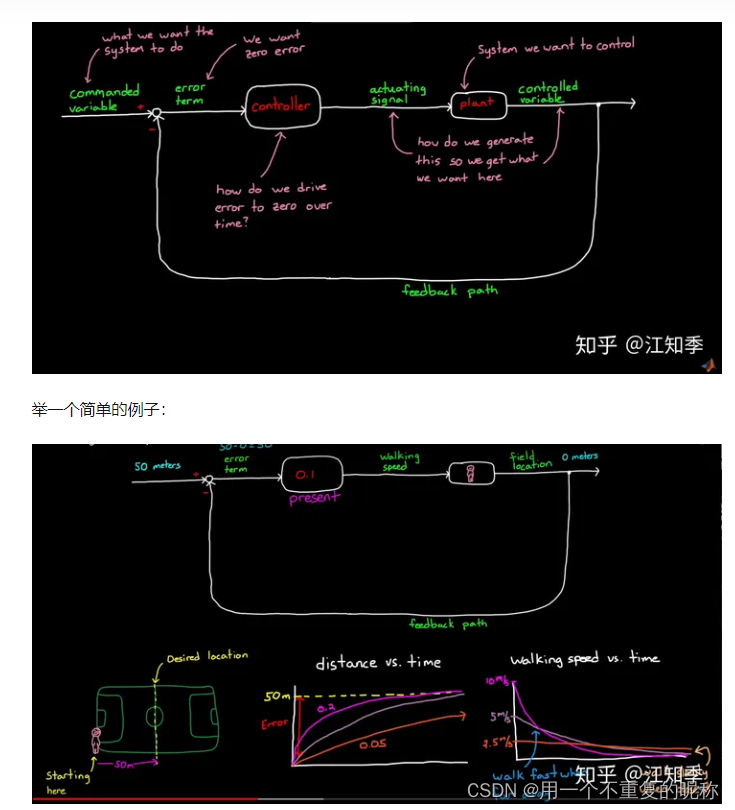
球场上运动至指定地点（比例控制）：有图【很直观的帮助理解】&有文字分析
2）初识PID-搞懂PID概念 https://zhuanlan.zhihu.com/p/74131690
【重点】数据有错误，但是跟着分析模拟了用p、pi、pid调控往水桶加水的过程
3）PID控制算法原理（抛弃公式，从本质上真正理解PID控制） https://zhuanlan.zhihu.com/p/39573490
看2）的时候 有时会看看3）帮助理解
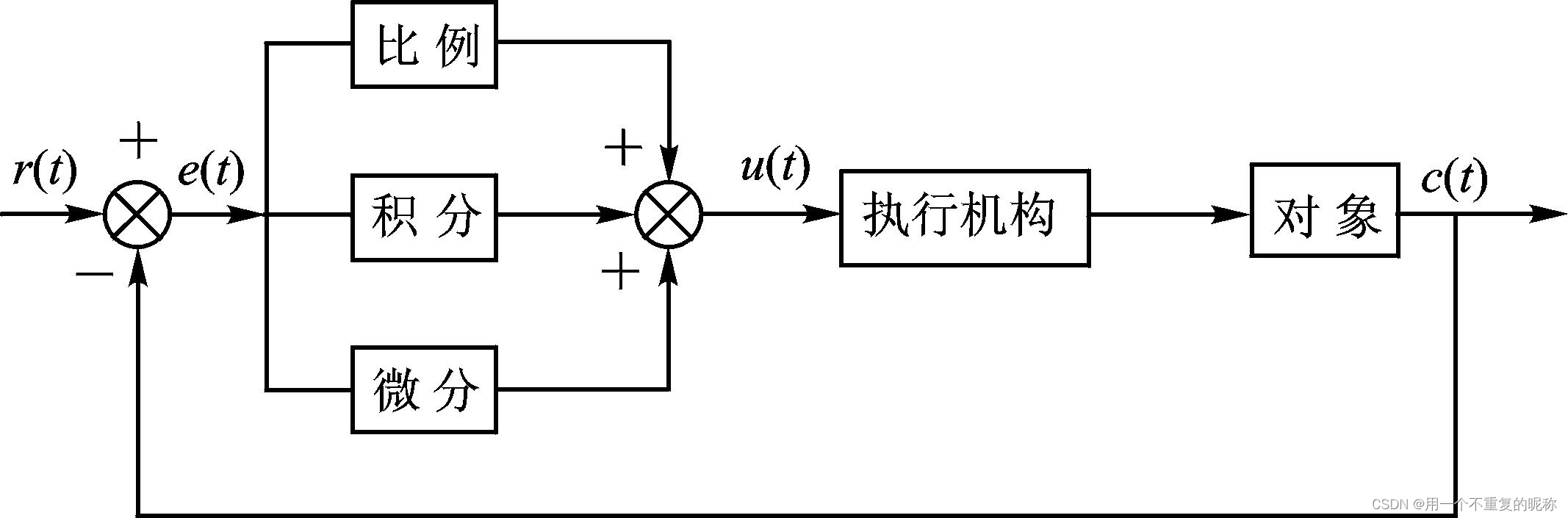
在这里插入图片描述
在这里插入图片描述
其中r(t)表示给定输入值，c(t)表示实际输出值，e(t)表示信号偏差量=r(t)-c(t)，u(t)表示修正量。 ------- https://www.cnblogs.com/cv-pr/p/4785195.html PID控制原理和算法。
PID调节器是一种线性调节器，它将给定值r(t)与实际输出值c(t)的偏差e(t)的比例§、积分(I)、微分(D)通过线性组合构成控制量u(t)，对控制对象进行控制。
在这里插入图片描述

代码实现与绘图：python3+matplotlib

import matplotlib.pyplot as plt
print(list(range(1,5))) # python3

# 参考  https://zhuanlan.zhihu.com/p/74131690
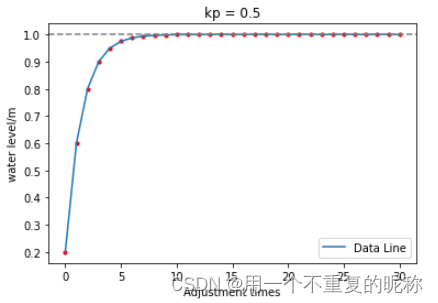
# (1)有个水桶,需要时刻保持1m 的高度,目前水桶里有0.2m 的水
# 采用P(比例) 的方法加水:即每次测量与1m 的误差,并加入与误差成比例的水量
# 比如设Kp=0.5.
# 第一次,误差是 1-0.2=0.8m,那么加入水量是 Kp*0.8= 0.4m

target = 1
now = 0.2
kp = 0.5

error_list = [0]
uk_list = [0]
now_list = [0.2]
add_num = 0
while add_num < 30:
    error = target-now
    error_list.append(error)
    uk = kp*error # 基于误差输出
    add_num += 1 
    uk_list.append(uk)
    now = now + uk
    now_list.append(now)

x=list(range(len(now_list)))
y=now_list
# 绘制折线图
plt.plot(x, y, label='Data Line')
# 绘制纵坐标线
plt.axhline(y=1, color='gray', linestyle='--')
# 绘制数据标记
for i in range(len(x)):
    # 绘制散点图
    plt.scatter(x[i], y[i], s=10, marker='o', color='red')
    # 用于标注文字，注释文本内容+被注释的坐标点+。。。
    # plt.annotate((x[i], y[i]), (x[i] + 0.1, y[i] - 0.051))
# 设置图表标题和标签
plt.title("kp = 0.5")
plt.xlabel("Adjustment times")
plt.ylabel("water level/m")
# 显示图表,得到一个带数据标记的折线图
plt.legend()
plt.show()
    
print("error_list={}, len(error_list)={}".format(error_list, len(error_list)))
print("uk_list={}, len(uk_list)={}".format(uk_list, len(uk_list)))
print("now_list={}, len(now_list)={}".format(now_list, len(now_list)))

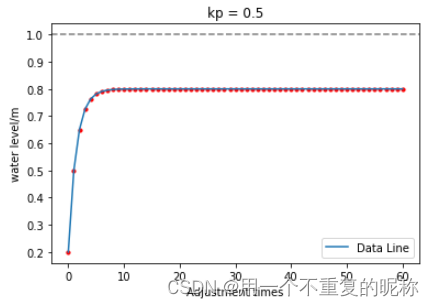
在这里插入图片描述

# (2) 新任务: 有个水桶,但桶底漏了个洞,仍需保持1m 的高度,
# 目前水桶里有0.2m 的水,但每次加水都会流出0.1m.
# 这个例子就接近我们实际工程的例子了,比如电机摩擦的阻力,损耗.
# 【】第一次仍是使用P (比例控制) u= Kp* e
target = 1
now = 0.2
kp = 0.5#1.9 #1 # 0.5

error_list = [0]
uk_list = [0]
now_list = [0.2]
add_num = 0
while add_num < 60:
    error = target-now
    error_list.append(error)
    uk = kp*error # 基于误差输出
    add_num += 1 
    uk_list.append(uk)
    now = now + uk - 0.1
    now_list.append(now)

x=list(range(len(now_list)))
y=now_list
# 绘制折线图
plt.plot(x, y, label='Data Line')
# 绘制纵坐标线
plt.axhline(y=1, color='gray', linestyle='--')
# 绘制数据标记
for i in range(len(x)):
    # 绘制散点图
    plt.scatter(x[i], y[i], s=10, marker='o', color='red')
    # 用于标注文字，注释文本内容+被注释的坐标点+。。。
    # plt.annotate((x[i], y[i]), (x[i] + 0.1, y[i] - 0.051))
# 设置图表标题和标签
plt.title("kp = 0.5")
plt.xlabel("Adjustment times")
plt.ylabel("water level/m")
# 显示图表,得到一个带数据标记的折线图
plt.legend()
plt.show()
    
print("error_list={}, len(error_list)={}".format(error_list, len(error_list)))
print("uk_list={}, len(uk_list)={}".format(uk_list, len(uk_list)))
print("now_list={}, len(now_list)={}".format(now_list, len(now_list)))

在这里插入图片描述

# (2) 新任务: 有个水桶,但桶底漏了个洞,仍需保持1m 的高度,
# 目前水桶里有0.2m 的水,但每次加水都会流出0.1m.
# 这个例子就接近我们实际工程的例子了,比如电机摩擦的阻力,损耗.
# 【】第一次仍是使用P (比例控制) u= Kp* e
target = 1
now = 0.2
kp = 1 #1.9 #1 # 0.5

error_list = [0]
uk_list = [0]
now_list = [0.2]
add_num = 0
while add_num < 60:
    error = target-now
    error_list.append(error)
    uk = kp*error # 基于误差输出
    add_num += 1 
    uk_list.append(uk)
    now = now + uk - 0.1
    now_list.append(now)

x=list(range(len(now_list)))
y=now_list
# 绘制折线图
plt.plot(x, y, label='Data Line')
# 绘制纵坐标线
plt.axhline(y=1, color='gray', linestyle='--')
# 绘制数据标记
for i in range(len(x)):
    # 绘制散点图
    plt.scatter(x[i], y[i], s=10, marker='o', color='red')
    # 用于标注文字，注释文本内容+被注释的坐标点+。。。
    # plt.annotate((x[i], y[i]), (x[i] + 0.1, y[i] - 0.051))
# 设置图表标题和标签
plt.title("kp = 1")
plt.xlabel("Adjustment times")
plt.ylabel("water level/m")
# 显示图表,得到一个带数据标记的折线图
plt.legend()
plt.show()
    
print("error_list={}, len(error_list)={}".format(error_list, len(error_list)))
print("uk_list={}, len(uk_list)={}".format(uk_list, len(uk_list)))
print("now_list={}, len(now_list)={}".format(now_list, len(now_list)))

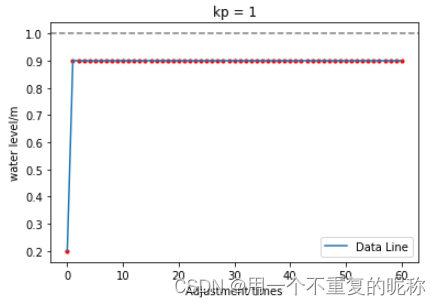
在这里插入图片描述

# (2) 新任务: 有个水桶,但桶底漏了个洞,仍需保持1m 的高度,
# 目前水桶里有0.2m 的水,但每次加水都会流出0.1m.
# 这个例子就接近我们实际工程的例子了,比如电机摩擦的阻力,损耗.
# 【】第一次仍是使用P (比例控制) u= Kp* e
target = 1
now = 0.2
kp = 1.9 #1.9 #1 # 0.5

error_list = [0]
uk_list = [0]
now_list = [0.2]
add_num = 0
while add_num < 60:
    error = target-now
    error_list.append(error)
    uk = kp*error # 基于误差输出
    add_num += 1 
    uk_list.append(uk)
    now = now + uk - 0.1
    now_list.append(now)

x=list(range(len(now_list)))
y=now_list
# 绘制折线图
plt.plot(x, y, label='Data Line')
# 绘制纵坐标线
plt.axhline(y=1, color='gray', linestyle='--')
# 绘制数据标记
for i in range(len(x)):
    # 绘制散点图
    plt.scatter(x[i], y[i], s=10, marker='o', color='red')
    # 用于标注文字，注释文本内容+被注释的坐标点+。。。
    # plt.annotate((x[i], y[i]), (x[i] + 0.1, y[i] - 0.051))
# 设置图表标题和标签
plt.title("kp = 1.9")
plt.xlabel("Adjustment times")
plt.ylabel("water level/m")
# 显示图表,得到一个带数据标记的折线图
plt.legend()
plt.show()
    
print("error_list={}, len(error_list)={}".format(error_list, len(error_list)))
print("uk_list={}, len(uk_list)={}".format(uk_list, len(uk_list)))
print("now_list={}, len(now_list)={}".format(now_list, len(now_list)))

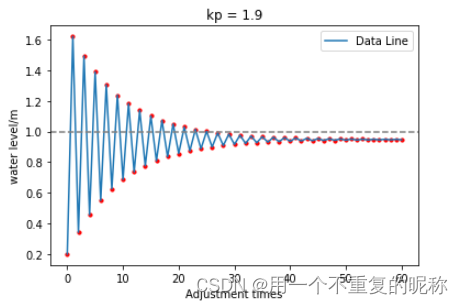
在这里插入图片描述

# 结论: 比例控制引入了稳态误差,且无法消除.
#       比例常数增大可以减小稳态误差,但如果太大则引起系统震荡,不稳定.
# 为了消除稳态误差,第二次加入积分,使用PI(比例积分控制) 
# 积分控制就是将历史误差全部加起来乘以积分常数.

target = 1
now = 0.2
kp = 0.5
ki = 0.5

error_list = [0]
uk_list = [0]
now_list = [0.2]
add_num = 0
history_error_list = [0]
ukp_list = [0]
uki_list = [0]
while add_num < 30:
    error = target-now
    error_list.append(error)
    ukp = kp*error # 比例部分
    ukp_list.append(ukp)
    history_error=sum(error_list)
    history_error_list.append(history_error)
    uki = ki*history_error #积分部分
    uki_list.append(uki)
    add_num += 1
    uk = ukp + uki #基于误差输出
    uk_list.append(uk)
    now = now + uk - 0.1
    now_list.append(now)

x=list(range(len(now_list)))
y=now_list
# 绘制折线图
plt.plot(x, y, label='Data Line')
# 绘制纵坐标线
plt.axhline(y=1, color='gray', linestyle='--')
# 绘制数据标记
for i in range(len(x)):
    # 绘制散点图
    plt.scatter(x[i], y[i], s=10, marker='o', color='red')
    # 用于标注文字，注释文本内容+被注释的坐标点+。。。
    # plt.annotate((x[i], y[i]), (x[i] + 0.1, y[i] - 0.051))
# 设置图表标题和标签
plt.title("kp = 0.5, ki = 0.5")
plt.xlabel("Adjustment times")
plt.ylabel("water level/m")
# 显示图表,得到一个带数据标记的折线图
plt.legend()
plt.show()    

print("error_list={}, len(error_list)={}".format(error_list, len(error_list)))
print("ukp_list={}, len(ukp_list)={}".format(ukp_list, len(ukp_list)))
print("uki_list={}, len(uki_list)={}".format(uki_list, len(uki_list)))
print("uk_list={}, len(uk_list)={}".format(uk_list, len(uk_list)))
print("now_list={}, len(now_list)={}".format(now_list, len(now_list)))

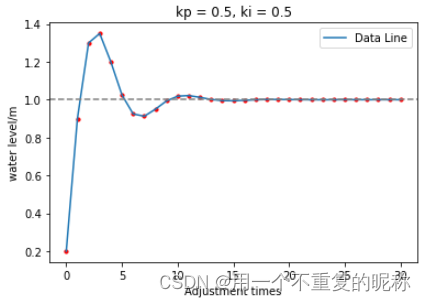
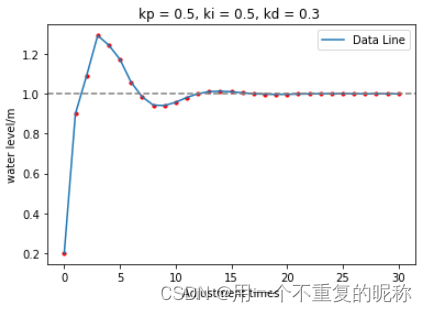
在这里插入图片描述

# 引入积分可以消除稳态误差,但会增加超调,且Ki 增大,超调量也增大.
# 为了消除超调,我们引入微分作用

target = 1
now = 0.2
kp = 0.5
ki = 0.5
kd = 0.3

error_list = [0]
uk_list = [0]
now_list = [0.2]
add_num = 0
history_error_list = [0]
ukp_list = [0]
uki_list = [0]
ukd_list = [0]
while add_num < 30:
    error = target-now
    error_list.append(error)
    ukp = kp*error # 比例部分
    ukp_list.append(ukp)
    history_error=sum(error_list)
    history_error_list.append(history_error)
    uki = ki*history_error #积分部分
    uki_list.append(uki)
    if add_num==0:
        diff_error=0
    else:
        diff_error=error_list[-1]-error_list[-2]
    ukd = kd*diff_error # 微分部分
    ukd_list.append(ukd)
    add_num += 1
    uk = ukp + uki + ukd #基于误差输出
    uk_list.append(uk)
    now = now + uk - 0.1
    now_list.append(now)

x=list(range(len(now_list)))
y=now_list
# 绘制折线图
plt.plot(x, y, label='Data Line')
# 绘制纵坐标线
plt.axhline(y=1, color='gray', linestyle='--')
# 绘制数据标记
for i in range(len(x)):
    # 绘制散点图
    plt.scatter(x[i], y[i], s=10, marker='o', color='red')
    # 用于标注文字，注释文本内容+被注释的坐标点+。。。
    # plt.annotate((x[i], y[i]), (x[i] + 0.1, y[i] - 0.051))
# 设置图表标题和标签
plt.title("kp = 0.5, ki = 0.5, kd = 0.3 ")
plt.xlabel("Adjustment times")
plt.ylabel("water level/m")
# 显示图表,得到一个带数据标记的折线图
plt.legend()
plt.show()       
    
print("error_list={}, len(error_list)={}".format(error_list, len(error_list)))
print("ukp_list={}, len(ukp_list)={}".format(ukp_list, len(ukp_list)))
print("uki_list={}, len(uki_list)={}".format(uki_list, len(uki_list)))
print("ukd_list={}, len(ukd_list)={}".format(ukd_list, len(ukd_list)))
print("uk_list={}, len(uk_list)={}".format(uk_list, len(uk_list)))
print("now_list={}, len(now_list)={}".format(now_list, len(now_list)))

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1248916.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

leetcode刷题日志-11盛最多水的容器

leetcode刷题日志-11盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线&#xff0c;第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线&#xff0c;使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明&#xff1a;你不能倾斜容器。 思路…
阅读更多...
LeetCode.88合并两个有序数组

LeetCode.88合并两个有序数组

LeetCode.88合并两个有序数组 1.问题描述2.解题思路3.代码 1.问题描述 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2&#xff0c;另有两个整数 m 和 n &#xff0c;分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中&#xff0c;使合并后的数组同…
阅读更多...
完美解决：Nginx访问PHP出现File not found.

完美解决：Nginx访问PHP出现File not found.

目录 解决方法一&#xff1a; 解决方法二&#xff1a; 遇到 File not found. 出现的问题解决&#xff1a; 解决方法一&#xff1a; 修改nginx的主配置文件。 vi /etc/nginx/nginx.conf location ~ \.php$ { root html; fastcgi_pass …
阅读更多...
人工智能-注意力机制之注意力提示

人工智能-注意力机制之注意力提示

注意力提示 自经济学研究稀缺资源分配以来&#xff0c;人们正处在“注意力经济”时代&#xff0c; 即人类的注意力被视为可以交换的、有限的、有价值的且稀缺的商品。 许多商业模式也被开发出来去利用这一点&#xff1a; 在音乐或视频流媒体服务上&#xff0c;人们要么消耗注意…
阅读更多...
读懂毛京波的营销，也就读懂了路特斯的提速转变

读懂毛京波的营销，也就读懂了路特斯的提速转变

“尽管我们交付还不到一年时间&#xff0c;但是今天Emeya一发布&#xff0c;我们的三车主又诞生了&#xff0c;他有Emira、Eletre&#xff0c;马上又定了Emeya&#xff0c;说明他对路特斯还是非常认可的&#xff0c;”路特斯集团CEO冯擎峰欣喜地说道&#xff0c;一个产品能不能…
阅读更多...
《C++PrimePlus》第8章 函数探幽

《C++PrimePlus》第8章 函数探幽

8.1 内联函数 使用内联函数 #include <iostream> using namespace std;inline double square(double x) { return x * x; }int main(){double a;a square(5.0);cout << "a " << a << endl;return 0; } 8.2 引用变量 将引用用作函数参数&…
阅读更多...
在JVM中 判定哪些对象是垃圾？

在JVM中 判定哪些对象是垃圾？

目录 垃圾的条件 1、引用计数法 2、可达性分析 3、强引用 4、软引用 5、弱引用 6、虚引用 判断垃圾的条件 在Java虚拟机&#xff08;JVM&#xff09;中&#xff0c;垃圾收集器负责管理内存&#xff0c;其中的垃圾收集算法用于确定哪些对象是垃圾&#xff0c;可以被回收…
阅读更多...
0002Java程序设计-springboot在线考试系统小程序

0002Java程序设计-springboot在线考试系统小程序

文章目录 **摘 要****目录**系统实现开发环境 编程技术交流、源码分享、模板分享、网课分享 企鹅&#x1f427;裙&#xff1a;776871563 摘 要 本毕业设计的内容是设计并且实现一个基于springboot的在线考试系统小程序。它是在Windows下&#xff0c;以MYSQL为数据库开发平台&…
阅读更多...
记一次linux操作系统实验

记一次linux操作系统实验

前言 最近完成了一个需要修改和编译linux内核源码的操作系统实验&#xff0c;个人感觉这个实验还是比较有意思的。这次实验总共耗时4天&#xff0c;从对linux实现零基础&#xff0c;通过查阅资料和不断尝试&#xff0c;直到完成实验目标&#xff0c;在这过程中确实也收获颇丰&…
阅读更多...
井盖位移监测系统怎么监测井盖位移

井盖位移监测系统怎么监测井盖位移

党的二十大报告提出&#xff0c;坚持人民城市人民建、人民城市为人民&#xff0c;提高城市规划、建设、治理水平。秉持依法治理、创新引领的理念&#xff0c;市政府应该坚定推进窨井盖安全管理工作&#xff0c;不断加大排查整治力度&#xff0c;弥补设施安全管理短板&#xff0…
阅读更多...
每日一练：“打家劫舍“（House Robber）问题 II

每日一练：“打家劫舍“（House Robber）问题 II

有想要了解打家劫舍初级问题的&#xff0c;可以点击下面链接查看&#xff01; 每日一练&#xff1a;“打家劫舍“&#xff08;House Robber&#xff09;问题 I 1. 问题 假设有房屋形成一个环形&#xff0c;即第一个房屋和最后一个房屋也相邻&#xff0c;每个房屋里都存放着一定…
阅读更多...
Java数组的复制、截取（内含例题：力扣-189.轮转数组）

Java数组的复制、截取（内含例题：力扣-189.轮转数组）

目录 数组的复制、截取&#xff1a; 1、使用Arrays中的copyOf方法完成数组的拷贝 2、使用Arrays中的copyofRange方法完成数组的拷贝 题目链接&#xff1a; 数组的复制、截取&#xff1a; 1、使用Arrays中的copyOf方法完成数组的拷贝 public class Csdn {public static vo…
阅读更多...
【Git】一文教你学会 submodule 的增、查、改、删

【Git】一文教你学会 submodule 的增、查、改、删

添加子模块 $ git submodule add <url> <path>url 为想要添加的子模块路径path 为子模块存放的本地路径 示例&#xff0c;添加 r-tinymaix 为子模块到主仓库 ./sdk/packages/online-packages/r-tinymaix 路径下&#xff0c;命令如下所示&#xff1a; $ git subm…
阅读更多...
UI自动化测试神器：RunnerGo测试平台

UI自动化测试神器：RunnerGo测试平台

可以直接进入官网下载开源版或点击右上角体验企业版体验 RunnerGo UI自动化平台 RunnerGo提供从API管理到API性能再到可视化的API自动化、UI自动化测试功能模块&#xff0c;覆盖了整个产品测试周期。 RunnerGo UI自动化基于Selenium浏览器自动化方案构建&#xff0c;内嵌高度…
阅读更多...
可持续创新 精选路线

可持续创新 精选路线

在加速企业数字化转型、 实现智能制造的升级之路上&#xff01; 使用好的工具固然重要&#xff0c; 而有好工具&#xff0c;也要会用工具。生信科技不仅为企业提供强大的产品支持&#xff0c; 更有全方位的定制化服务&#xff0c; 提升工程师的工具应用能力&#xff0c; 让企业…
阅读更多...
海外https代理ip如何保障信息安全？该怎么选择？

海外https代理ip如何保障信息安全？该怎么选择？

海外https代理ip是指通信协议为https的海外真实网络地址ip&#xff0c;通常应用在各种跨境业务中。 一、什么是HTTPS协议 HTTP协议是一个应用层协议&#xff0c;通常运行在TCP协议之上。它是一个明文协议&#xff0c;客户端发起请求&#xff0c;服务端给出响应的响应。由于网…
阅读更多...
pat实现基于邻接表表示的深度优先遍历[含非递归写法]

pat实现基于邻接表表示的深度优先遍历[含非递归写法]

文章目录 1.递归2.非递归 1.递归 void DFS(ALGraph G, int v) {visited[v] 1;printf("%c ", G.vertices[v].data);for (ArcNode* cur G.vertices[v].firstarc; cur ! nullptr; cur cur->nextarc){if (!visited[cur->adjvex])DFS(G, cur->adjvex);} }2.非…
阅读更多...
matlab画双坐标图的样式

matlab画双坐标图的样式

matlab画双坐标图的样式 %% clc,clear,close all; t0:0.1:9*pi; figure; [AX,Ha,Hb]plotyy(t,sin(t),t,exp(t)); % 绘图并创建句柄 % ----------------- 设置刻度 set(AX(1),yTick,[-1.250:0.25:1.25]) % 设置左边Y轴的刻度 set(AX(2),yTick,[0:50:350]) …
阅读更多...
2023年【危险化学品经营单位安全管理人员】考试内容及危险化学品经营单位安全管理人员最新解析

2023年【危险化学品经营单位安全管理人员】考试内容及危险化学品经营单位安全管理人员最新解析

题库来源&#xff1a;安全生产模拟考试一点通公众号小程序 危险化学品经营单位安全管理人员考试内容是安全生产模拟考试一点通生成的&#xff0c;危险化学品经营单位安全管理人员证模拟考试题库是根据危险化学品经营单位安全管理人员最新版教材汇编出危险化学品经营单位安全管…
阅读更多...
HarmonyOS开发：ArkTs常见数据类型

HarmonyOS开发：ArkTs常见数据类型

前言 无论是Android还是iOS开发&#xff0c;都提供了多种数据类型用于常见的业务开发&#xff0c;但在ArkTs中&#xff0c;数据类型就大有不同&#xff0c;比如int&#xff0c;float&#xff0c;double&#xff0c;long统一就是number类型&#xff0c;当然了也不存在char类型&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023