仅作自己学习使用
一、问题
需求: 计算函数
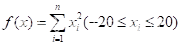
的极小值,其中个体x的维数n=10,即x=(x1,x2,…,x10),其中每一个分量xi均需在[-20,20]内。因此可以知道,这个函数只有一个极小值点x = (0,0,…,0),且其极小值是0,那么我们用模拟退火来实现一下:
二、matlab代码实现
clear
clc
T1 = cputime;
D = 10; % 变量维数
Xs = 20; % 上限
Xx = -20; % 下限
L = 20; % 马尔可夫链长度
K = 0.98; % 降温系数
S = 0.01; % 步长因子
T = 100; % 初始温度
YZ = 1e-8; % 容差
P = 0; % MetroPolis过程中总接受点(MetroPolis是接受准则,小于接受,大于是概率接受)
PreX = rand(D,1)*(Xs-Xx) + Xx; % 设置初值位置(这个随机数可以产生一个-20到20的随机数)
PreBestX = PreX; % 上一个最优解
PreX = rand(D,1)*(Xs-Xx) + Xx; % 虽然代码相同,但是因为随机数种子,产生的值会不同
BestX = PreX; % 最优解
trace = eval(BestX); % 记录初始值
deta = abs(eval(BestX) - eval(PreBestX));
while (deta>YZ) && (T>0.0001)
%% 本次退火结束,降温
T = K * T;
%% 在当前温度T下的迭代次数为L
for i = 1 : L
% 在此点附近随机选择下一个点
NextX = PreX + S*(rand(D,1)*(Xs-Xx) + Xx);
% 如果这个点其中有个分量超出了定义域,则重新分配一个值
for j = 1:D
if(NextX(j) > Xs || NextX(j)<Xx)
NextX(j) = PreX(j) + S*(rand*(Xs-Xx) + Xx);
j = j-1; % 因为重新分配的值任然可能超出边界,所以退回到当前的那个j,再次检查是否超出边界
end
end
%% 判断是否是全局最优解
if( eval(NextX) < eval(BestX) )
PreBestX = BestX; % 保留上一个最优解
BestX = NextX; % 更新上一个最优解
end
%% MetroPolis接受准则
if( eval(NextX) < eval(PreX) )
% 当前解更优秀,接受新解
PreX = NextX;
P = P + 1;
else
% 当前解更差,概率接受
P1 = exp((eval(PreX)-eval(NextX))/T); % 注意指数部分是个复数,所以要自己调整减的顺序
if (P1 > rand)
PreX = NextX;
P = P + 1;
end
end
trace = [trace eval(BestX)];
end
deta = abs(eval(BestX)-eval(PreBestX));
end
T2 = cputime;
% 运行代码所需要的CPU时间
timeConsume = T2 - T1;
disp('最小值点在:');
BestX
disp('最小值为');
eval(BestX)
figure(color=[1 1 1])
plot(trace(2:end),Color=[0.502, 0.000, 0.502],LineWidth=2);
xlabel("迭代次数")
ylabel("目标函数值")
title("适应度曲线","CPU时间消耗: "+timeConsume + 's');
function result = eval(x)
%% 评估函数
result = sum(x.^2);
end
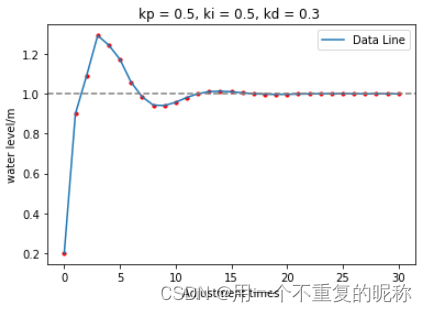
三、效果图
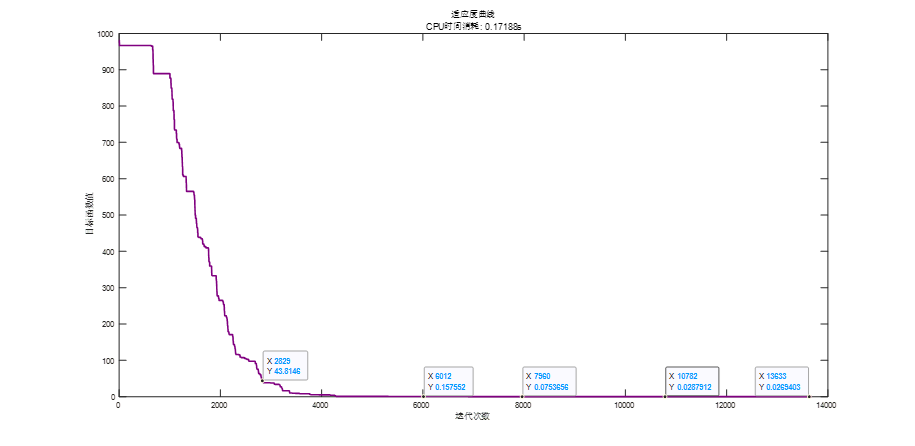
可以看到,最后是达到0.0269403,还不是真正意义上的极小值,但是模拟退火算法也算是一个比较有效的全局搜索算法了。