scipy.interpolate插值方法

1 一维插值

from scipy.interpolate import interp1d
1维插值算法

from scipy.interpolate import interp1d
x = np.linspace(0, 10, num=11, endpoint=True)
y = np.cos(-x**2/9.0)
f = interp1d(x, y)
f2 = interp1d(x, y, kind='cubic')
xnew = np.linspace(0, 10, num=41, endpoint=True)
import matplotlib.pyplot as plt
plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
plt.legend(['data', 'linear', 'cubic'], loc='best')
plt.show()

数据点，线性插值结果，cubic插值结果：
在这里插入图片描述

2 multivariate data

from scipy.interpolate import interp2d

from scipy.interpolate import griddata
多为插值方法，可以应用在2Dlut，3Dlut的生成上面，比如当我们已经有了两组RGB映射数据, 可以插值得到一个查找表。

二维插值的例子如下：

import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt

from scipy.interpolate import griddata, RegularGridInterpolator, Rbf

if __name__ == "__main__":
    x_edges, y_edges = np.mgrid[-1:1:21j, -1:1:21j]
    x = x_edges[:-1, :-1] + np.diff(x_edges[:2, 0])[0] / 2.
    y = y_edges[:-1, :-1] + np.diff(y_edges[0, :2])[0] / 2.

    # x_edges, y_edges 是 20个格的边缘的坐标， 尺寸 21 * 21
    # x, y 是 20个格的中心的坐标， 尺寸 20 * 20

    z = (x + y) * np.exp(-6.0 * (x * x + y * y))

    print(x_edges.shape, x.shape, z.shape)
    plt.figure()
    lims = dict(cmap='RdBu_r', vmin=-0.25, vmax=0.25)
    plt.pcolormesh(x_edges, y_edges, z, shading='flat', **lims) # plt.pcolormesh(), plt.colorbar() 画图
    plt.colorbar()
    plt.title("Sparsely sampled function.")
    plt.show()

    # 使用grid data
    xnew_edges, ynew_edges = np.mgrid[-1:1:71j, -1:1:71j]
    xnew = xnew_edges[:-1, :-1] + np.diff(xnew_edges[:2, 0])[0] / 2. # xnew其实是 height new
    ynew = ynew_edges[:-1, :-1] + np.diff(ynew_edges[0, :2])[0] / 2.
    grid_x, grid_y = xnew, ynew

    print(x.shape, y.shape, z.shape)
    points = np.hstack((x.reshape(-1, 1), y.reshape(-1, 1)))
    z1 = z.reshape(-1, 1)

    grid_z0 = griddata(points, z1, (grid_x, grid_y), method='nearest').squeeze()
    grid_z1 = griddata(points, z1, (grid_x, grid_y), method='linear').squeeze()
    grid_z2 = griddata(points, z1, (grid_x, grid_y), method='cubic').squeeze()

    rbf = Rbf(points[:, 0], points[:, 1], z, epsilon=2)
    grid_z3 = rbf(grid_x, grid_y)

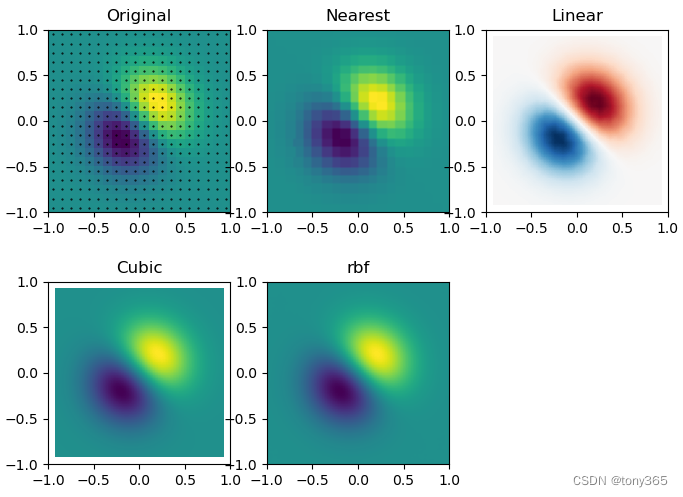
    plt.subplot(231)
    plt.imshow(z.T, extent=(-1, 1, -1, 1), origin='lower')
    plt.plot(points[:, 0], points[:, 1], 'k.', ms=1)
    plt.title('Original')
    plt.subplot(232)
    plt.imshow(grid_z0.T, extent=(-1, 1, -1, 1), origin='lower')
    plt.title('Nearest')
    plt.subplot(233)
    plt.imshow(grid_z1.T, extent=(-1, 1, -1, 1), origin='lower', cmap='RdBu_r')
    plt.title('Linear')
    plt.subplot(234)
    plt.imshow(grid_z2.T, extent=(-1, 1, -1, 1), origin='lower')
    plt.title('Cubic')
    plt.subplot(235)
    plt.imshow(grid_z3.T, extent=(-1, 1, -1, 1), origin='lower')
    plt.title('rbf')
    plt.gcf().set_size_inches(8, 6)
    plt.show()

在这里插入图片描述

示例2：

def func(x, y):
    return x*(1-x)*np.cos(4*np.pi*x) * np.sin(4*np.pi*y**2)**2


grid_x, grid_y = np.mgrid[0:1:100j, 0:1:200j]


rng = np.random.default_rng()
points = rng.random((1000, 2))
values = func(points[:,0], points[:,1])

from scipy.interpolate import griddata
grid_z0 = griddata(points, values, (grid_x, grid_y), method='nearest')
grid_z1 = griddata(points, values, (grid_x, grid_y), method='linear')
grid_z2 = griddata(points, values, (grid_x, grid_y), method='cubic')

import matplotlib.pyplot as plt
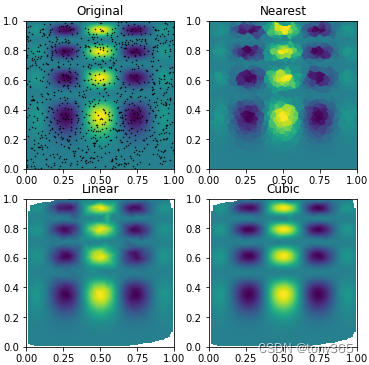
plt.subplot(221)
plt.imshow(func(grid_x, grid_y).T, extent=(0,1,0,1), origin='lower')
plt.plot(points[:,0], points[:,1], 'k.', ms=1)
plt.title('Original')
plt.subplot(222)
plt.imshow(grid_z0.T, extent=(0,1,0,1), origin='lower')
plt.title('Nearest')
plt.subplot(223)
plt.imshow(grid_z1.T, extent=(0,1,0,1), origin='lower')
plt.title('Linear')
plt.subplot(224)
plt.imshow(grid_z2.T, extent=(0,1,0,1), origin='lower')
plt.title('Cubic')
plt.gcf().set_size_inches(6, 6)
plt.show()

在这里插入图片描述

3 Multivariate data interpolation on a regular grid

from scipy.interpolate import RegularGridInterpolator

已知一些grid上的值。
可以应用在2Dlut，3Dlut，当我们已经有了一个多维查找表，然后整个图像作为输入，得到查找和插值后的输出。

二维网格插值方法（好像和resize的功能比较一致）

# 使用RegularGridInterpolator
import matplotlib.pyplot as plt
from scipy.interpolate import RegularGridInterpolator

def F(u, v):
    return u * np.cos(u * v) + v * np.sin(u * v)

fit_points = [np.linspace(0, 3, 8), np.linspace(0, 3, 8)]
values = F(*np.meshgrid(*fit_points, indexing='ij'))

ut, vt = np.meshgrid(np.linspace(0, 3, 80), np.linspace(0, 3, 80), indexing='ij')
true_values = F(ut, vt)
test_points = np.array([ut.ravel(), vt.ravel()]).T

interp = RegularGridInterpolator(fit_points, values)
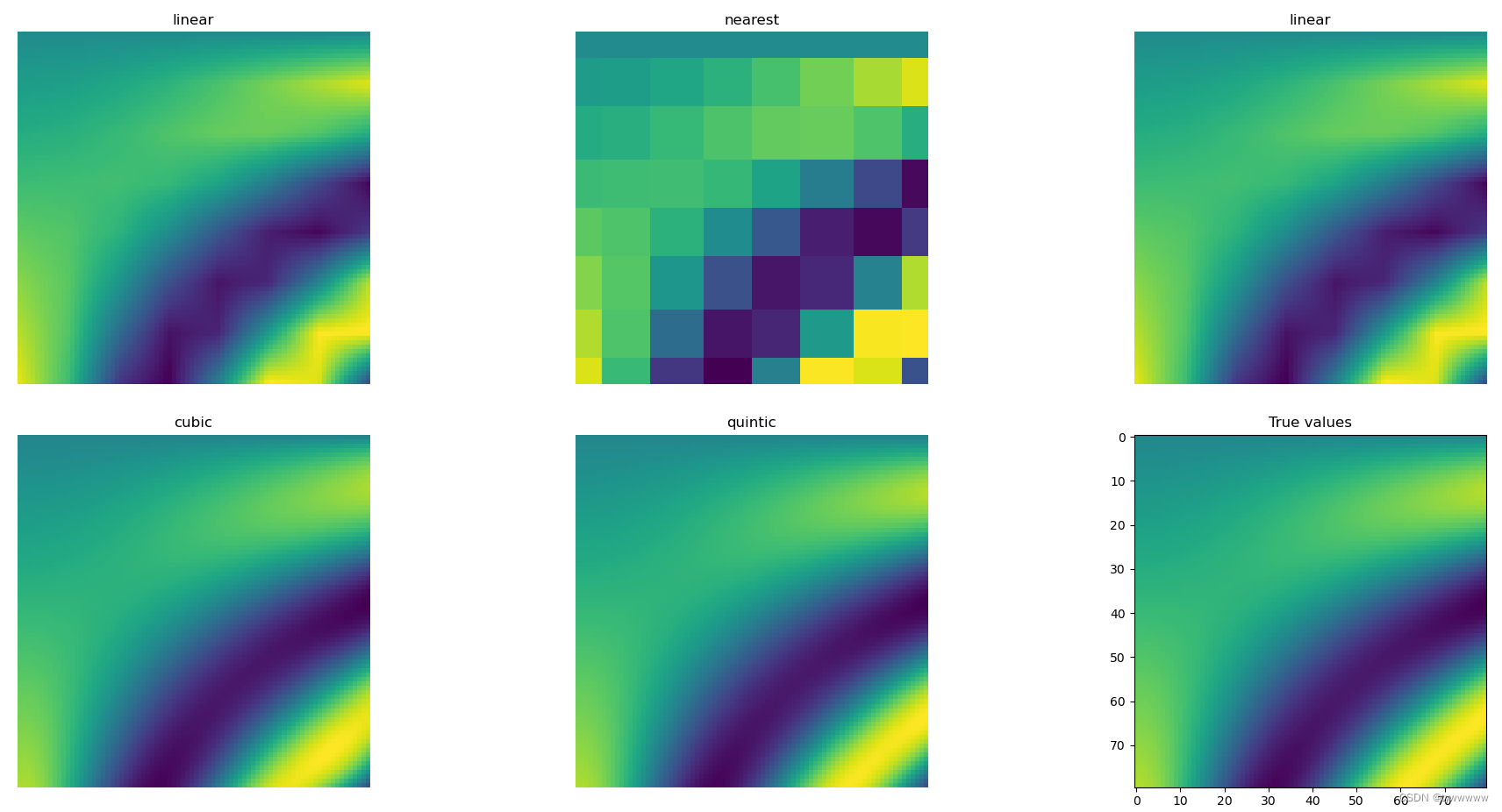
fig, axes = plt.subplots(2, 3, figsize=(10, 6))
axes = axes.ravel()
fig_index = 0
for method in ['linear', 'nearest', 'linear', 'cubic', 'quintic']:
    im = interp(test_points, method=method).reshape(80, 80)
    axes[fig_index].imshow(im)
    axes[fig_index].set_title(method)
    axes[fig_index].axis("off")
    fig_index += 1
axes[fig_index].imshow(true_values)
axes[fig_index].set_title("True values")
fig.tight_layout()
fig.show()
plt.show()

在这里插入图片描述

4 Rbf 插值方法

interpolate scattered 2-D data

import numpy as np
from scipy.interpolate import Rbf
import matplotlib.pyplot as plt
from matplotlib import cm

# 2-d tests - setup scattered data
rng = np.random.default_rng()
x = rng.random(100) * 4.0 - 2.0
y = rng.random(100) * 4.0 - 2.0
z = x * np.exp(-x ** 2 - y ** 2)


edges = np.linspace(-2.0, 2.0, 101)
centers = edges[:-1] + np.diff(edges[:2])[0] / 2.

XI, YI = np.meshgrid(centers, centers)
# use RBF
rbf = Rbf(x, y, z, epsilon=2)
Z1 = rbf(XI, YI)

points = np.hstack((x.reshape(-1, 1), y.reshape(-1, 1)))
Z2 = griddata(points, z, (XI, YI), method='cubic').squeeze()

# plot the result
plt.figure(figsize=(20,8))
plt.subplot(1, 2, 1)
X_edges, Y_edges = np.meshgrid(edges, edges)
lims = dict(cmap='RdBu_r', vmin=-0.4, vmax=0.4)
plt.pcolormesh(X_edges, Y_edges, Z1, shading='flat', **lims)
plt.scatter(x, y, 100, z, edgecolor='w', lw=0.1, **lims)
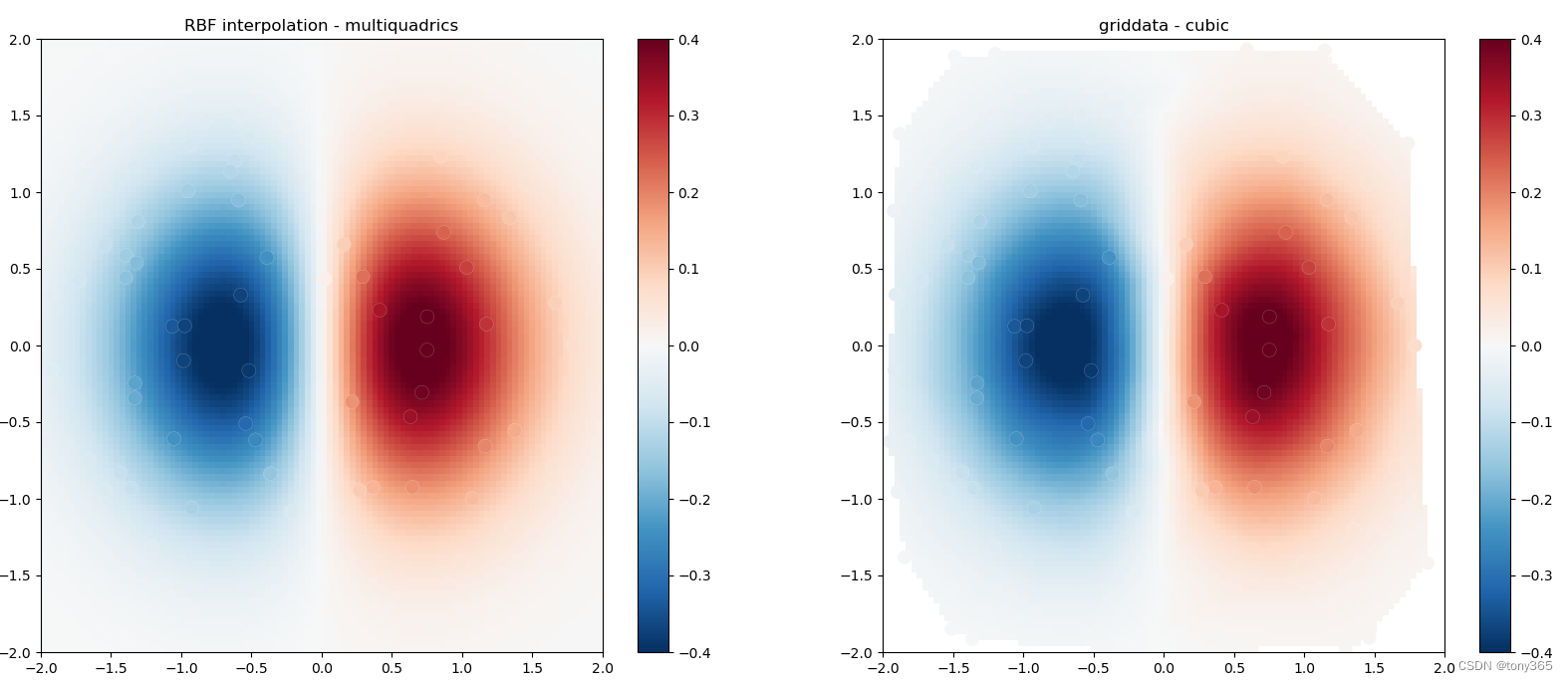
plt.title('RBF interpolation - multiquadrics')
plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.colorbar()

plt.subplot(1, 2, 2)
X_edges, Y_edges = np.meshgrid(edges, edges)
lims = dict(cmap='RdBu_r', vmin=-0.4, vmax=0.4)
plt.pcolormesh(X_edges, Y_edges, Z2, shading='flat', **lims)
plt.scatter(x, y, 100, z, edgecolor='w', lw=0.1, **lims)
plt.title('griddata - cubic')
plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.colorbar()
plt.show()