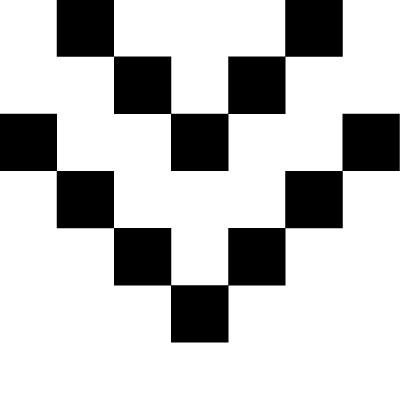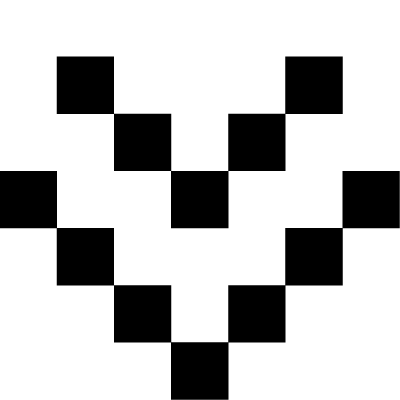原题解答

本次的题目如下所示（原题出处：NOC）：

角谷猜想：以一个正整数n为例，如果n为偶数，就将它变为n/2；如果除后变成奇数，则将它乘3加1（即3n+1）。不断重复这样的操作，经过有限步后，必然会得到1。

输入：一个正整数

输出：变成1经过的步骤数

输入样例：24

输出样例：10

本题是数论猜想验证类的题型。在数学的数论领域，有很多未被证明的猜想，称为我们的编程题。数论的题目有一个特点，所有的数据必然是自然数。因此我们需要注意此类题目中出现除法就代表整除。 

现在针对这道题我们说一下思路。本题中需要经过多少步才能得到结果我们事先并不知道，因此只能使用while循环。既然是等于1为终止条件，那循环的条件就是不等于1。

循环体中只有两种可能性，要么n为偶数，则整除2；要么n为奇数，则要乘三加一。无论是奇数还是偶数，只要循环一次，计数就要加1。

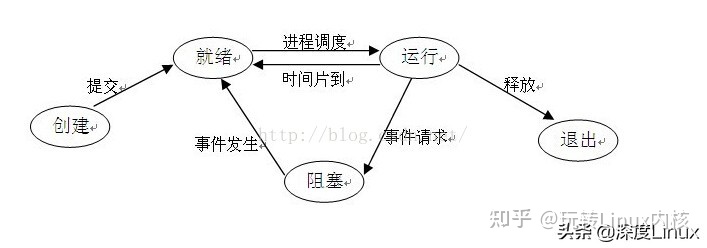
根据这个条件，我们很轻松就可以得到流程图如下：

 

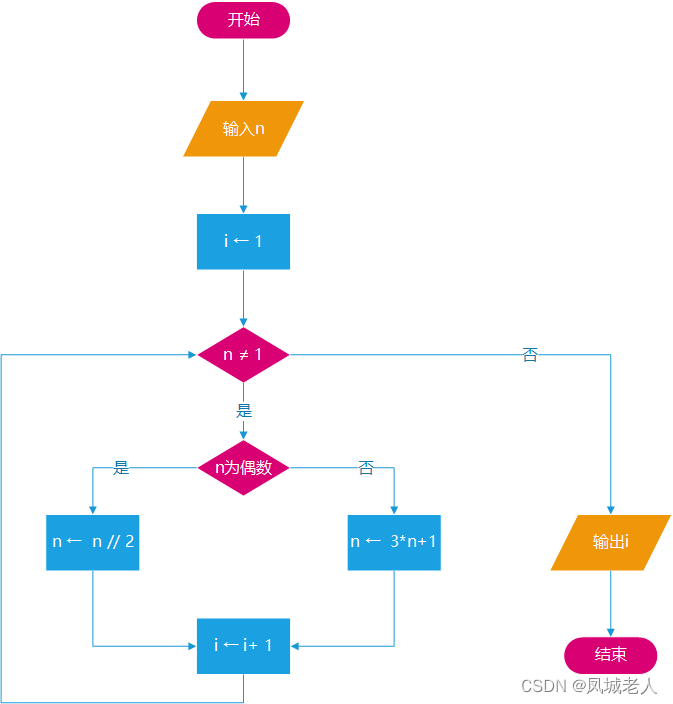
 题目的Python代码如下所示：

n = int(input())
i = 0
while n != 1:
    if n % 2 == 0:
        n //= 2
    else:
        n = 3 * n + 1
    i += 1
print(i)

本题拓展

本道题主要考查的知识点为条件循环和分支结构，题目难度：★★

遇到此类问题，我们只要知道题目中表达定理或猜想的含义，按照步骤操作即可。本题我们可以做一定的修改，即可变成另外一道题：

角谷猜想：以一个正整数n为例，如果n为偶数，就将它变为n/2；如果除后变成奇数，则将它乘3加1（即3n+1）。不断重复这样的操作，经过有限步后，必然会得到1。

输入：一个正整数

输出：变成1经过的所有数，以空格隔开

输入样例：24

输出样例：24 12 6 3 10 5 16 8 4 2 1

本题的思路与原题基本一致， 区别在于需要将中途经过的所有数都打印出来。整体思路保持不变，仅需将累加改为每次打印出n。注意：原始数据循环后即发生变化，因此在循环开始前需要先打印一次，代码如下：

n = int(input())
print(n, end=' ')
while n != 1:
    if n % 2 == 0:
        n //= 2
    else:
        n = 3 * n + 1
    print(n, end=' ')