对GNN的评估
GNN 通用表达式
聚合:
a v ( k ) = A G G R E A G T E ( k ) ( { h u ( k − 1 ) : u ∈ N ( v ) } ) a_v^{(k)}=AGGREAGTE^{(k)}(\{ h_u^{(k-1)} : u \in \mathcal{N}(v) \}) av(k)=AGGREAGTE(k)({hu(k−1):u∈N(v)})
更新:
h v ( k ) = C O M B I N E ( k ) ( h v ( k − 1 ) , a v ( k ) ) h_v^{(k)} = COMBINE^{(k)}(h_v^{(k-1)},a_v^{(k)}) hv(k)=COMBINE(k)(hv(k−1),av(k))
GNN 的主要任务
节点分类任务:相同邻域有相同表征,不同的邻域有不同的表征
图分类任务:同构图有相同的表征,非同构图有不同的表征
定义1 multiset的广义定义:允许其元素有多个实例的集合。
multiset是一个二元组 X = ( S , m ) X = (S, m) X=(S,m)
- S 是由不同元素形成的X的基础集合
- m : S → N ≥ 1 m : S \rightarrow N_{\ge 1} m:S→N≥1 给出了元素的 multiset
举个例子,节点集合是S,每个节点的邻居集合是m
引理2 假设 G1 和 G2 是两个不同构的图。如果对于一个GNN模型 A, G1 和 G2 有着不同的嵌入,那么WL图同构检测也能得到同样的结果。
引理2说明:任何基于聚合的GNN的效果天花板是WL算法。
WL测试:有效且计算高效的检测图同构算法
- 迭代地聚合节点及其邻居的标签
- 哈希聚合的标签为新的标签
- 对比标签,如果在某次迭代中两个图的节点标签不同则不是同构的
定理3 假设 A 是一个GNN模型。如果由足够多的GNN层,A 能够将任何WL算法检测为非同构的图 G1 和 G2 表达为不同的嵌入。同时,这需要满足以下约束:
- A 通过
h
v
(
k
)
=
ϕ
(
h
v
(
k
−
1
)
,
f
(
{
h
u
(
k
−
1
)
:
u
∈
N
(
v
)
}
)
)
h_v^{(k)} = \phi (h_v^{(k-1)}, f(\{ h_u^{(k-1)} : u \in N(v) \}))
hv(k)=ϕ(hv(k−1),f({hu(k−1):u∈N(v)})) 迭代地聚合和更新节点特征
- 其中, f f f作用于multiset, ϕ \phi ϕ是单射的
- A 的 graph-level readout (作用于节点特征 { h v ( k ) } \{ h_v^{(k)} \} {hv(k)}的multiset) 是单射的
Readout函数:输入节点嵌入生成整图嵌入的函数
定理3说明:如果聚合邻居的函数和graph-level readout函数是单射的,那么GNN的结果可以和WL算法一样好
引理4 假设输入的特征空间 X \mathcal{X} X 是可数的,如果 g ( k ) g^{(k)} g(k) 是由GNN的第k层参数化的函数 (k=1,2,3,…,L, g ( 1 ) g^{(1)} g(1)定义在有界的multiset X ⊂ X X \subset \mathcal{X} X⊂X 上),那么 g ( k ) g^{(k)} g(k) 的范围也是可数的 (对于k=1,2,3,…,L)
疑惑:是在讲收敛性吗?
GNN 相比 WL 的优势
- 由于WL算法的节点特征向量本质上是one-hot encodings,因此无法得知子树的相似性。
- 疑问:多次迭代不就可以知道n阶邻居的信息了吗,是因为哈希方法处理特征所以无法有效保存结构信息吗?
- 但满足定理3的GNN模型可以获得图结构的相似性,学习为子树生成低维嵌入。
Graph Isomorphism Network (GIN)
GIN满足定理3,是WL算法的推广,因此取得了一众GNN中最好的判别效果
引理5 假设 X \mathcal{X} X 是可数的。那么存在一个函数 f : X → R n f : \mathcal{X} \rightarrow \R ^n f:X→Rn 使得 h ( X ) = ∑ x ∈ X f ( x ) h(X) = \sum_{x \in X} f(x) h(X)=∑x∈Xf(x) 对于每一个有界的multiset x ⊂ X x \subset \mathcal{X} x⊂X 是唯一的。此外,对于某些函数 ϕ \phi ϕ ,任何 multiset 函数 g 都可以被分解为 g ( X ) = ϕ ( ∑ x ∈ X f ( x ) ) g(X) = \phi (\sum _{x \in X} f(x)) g(X)=ϕ(∑x∈Xf(x)) 。
引理5说明:累加聚合器是单射的,是multiset的通用函数
推论6 假设 X \mathcal{X} X 是可数的。那么存在一个函数 f : X → R n f : \mathcal{X} \rightarrow \R ^n f:X→Rn ,对于 ϵ \epsilon ϵ 的无限个选择 (包含所有无理数) ,对于每一对 ( c , X ) (c,X) (c,X) , h ( c , X ) = ( 1 + ϵ ) ⋅ f ( c ) + ∑ x ∈ X f ( x ) h(c, X) = (1+\epsilon) \cdot f(c) + \sum_{x \in X} f(x) h(c,X)=(1+ϵ)⋅f(c)+∑x∈Xf(x) 是唯一的 (其中 c ∈ X , X ⊂ X c \in \mathcal{X}, X \subset \mathcal{X} c∈X,X⊂X)。此外,对于一些函数, ( c , X ) (c,X) (c,X) 上的任何函数都可以被分解为 g ( c , X ) = φ ( ( 1 + ϵ ) ⋅ f ( c ) + ∑ x ∈ X f ( x ) ) g(c, X) = \varphi ((1 + \epsilon) \cdot f(c) + \sum_{x \in X} f(x)) g(c,X)=φ((1+ϵ)⋅f(c)+∑x∈Xf(x))。
推论6在众多聚合方案中提供了一个简单而具体的公式。
GIN 更新公式 - 节点:
h v ( k ) = M L P ( k ) ( ( 1 + ϵ ( k ) ) ⋅ h v ( k − 1 ) + ∑ u ∈ N ( v ) h u ( k − 1 ) ) h_v^{(k)} = MLP^{(k)} ((1 + \epsilon^{(k)}) \cdot h_v^{(k-1)} + \sum_{u \in \mathcal{N}(v)} h_u^{(k-1)}) hv(k)=MLP(k)((1+ϵ(k))⋅hv(k−1)+u∈N(v)∑hu(k−1))
- MLP : 多层感知机
- ϵ \epsilon ϵ : 可学习的参数或固定值
GIN Readout函数 - 整图:
h G = C O N C A T ( R E A D O U T ( { h v ( k ) ∣ v ∈ G } ) ∣ k = 0 , 1 , . . . , K ) h_G = CONCAT(READOUT(\{ h_v^{(k)} | v \in G \}) | k=0,1,...,K ) hG=CONCAT(READOUT({hv(k)∣v∈G})∣k=0,1,...,K)
通过定理3 和 推论6 可知,如果使用上式作为readout函数(累加相同迭代的所有节点特征作为图的表征),那么它是WL的推广。
GNN方法对比
单层感知机 vs 多层感知机
引理7 存在有限个multiset X 1 ≠ X 2 X_1 \neq X_2 X1=X2 ,对于任何线性映射 W, ∑ x ∈ X 1 R e L U ( W x ) = ∑ x ∈ X 2 R e L U ( W x ) \sum _{x \in X_1} ReLU(Wx) = \sum_{x\in X_2} ReLU(Wx) ∑x∈X1ReLU(Wx)=∑x∈X2ReLU(Wx) 。
引理7说明:存在仅用单层感知机的模型永远无法区分的网络邻域 (multiset)
- 缺少偏置项的单层感知机类似于线性映射,GNN层退化为仅仅累加邻居特征,引理7就是基于此证明得到的。
- 相比MLPs,单层感知机 (即使存在偏置项) 就算能够在某种程度上嵌入不同的图到不同的位置,依然难以捕获结构的相似性,因此难以完成分类任务。
聚合方法对比 - Mean && Max && Sum
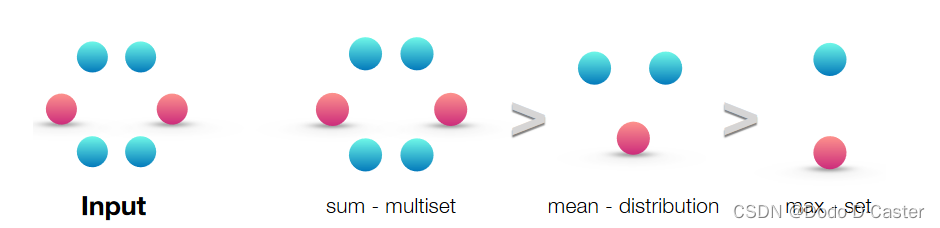
- sum 捕获完整的multiset
- mean 捕获multiset中元素的分布 / 比例
- max 则忽略了多样性,将multiset简化为一个简单的集合
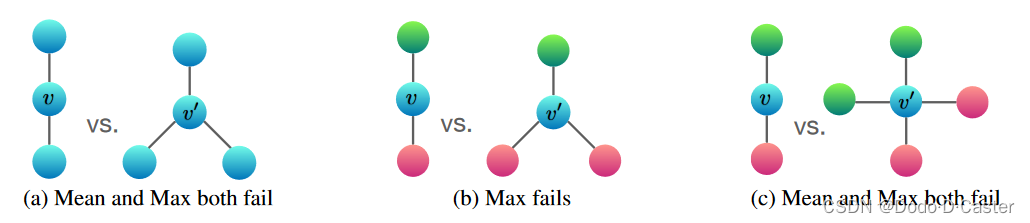
- (a) 图的两种结构使用mean和max无法区分
- (b) 图的两种结构使用max无法区分
- © 图的两种结构使用mean和max无法区分
Mean和Max方法是置换不变的,但不是单射的。而三种方法中,Sum方法更接近偏向单射。
Mean
推论8 假设 X \mathcal{X} X 是可数的。存在一个函数 f : X → R n f : \mathcal{X} \rightarrow \R ^n f:X→Rn 使得当且仅当 X 1 X_1 X1 和 X 2 X_2 X2 有着相同的分布时, h ( X ) = 1 ∣ X ∣ ∑ x ∈ X f ( x ) , h ( X 1 ) = h ( X 2 ) h(X) = \frac{1}{|X|} \sum _{x \in X} f(x), h(X_1) = h(X_2) h(X)=∣X∣1∑x∈Xf(x),h(X1)=h(X2) 。也就是说,假设 ∣ X 2 ∣ ≥ ∣ X 1 ∣ |X_2| \ge |X_1| ∣X2∣≥∣X1∣ ,那么,对于一些 k ∈ N ≥ 1 k \in \N _{\ge 1} k∈N≥1 ,我们有 X 1 = ( S , m ) X_1 = (S,m) X1=(S,m) 和 X 2 = ( S , k ⋅ m ) X_2 = (S, k \cdot m) X2=(S,k⋅m) 。
该定理说明了使用Mean无法区分的情况,对于Mean而言:
- X 1 = ( S , m ) X_1 = (S,m) X1=(S,m) 和 X 2 = ( S , k ⋅ m ) X_2 = (S, k \cdot m) X2=(S,k⋅m) 时, X 1 = X 2 X_1 = X_2 X1=X2 。( k ⋅ m k \cdot m k⋅m 表示有k个m的复制 )
- 捕获的只是邻居特征的分布
- 适合节点分类任务,因为在这类任务节点的特征丰富,并且邻域特征的分布有着巨大的重要性
Max
推论9 假设 X \mathcal{X} X 是可数的。存在一个函数 f : X → R ∞ f : \mathcal{X} \rightarrow \R ^{\infty} f:X→R∞ 使得得当且仅当 X 1 X_1 X1 和 X 2 X_2 X2 有着相同的基础集时, h ( X ) = M A X x ∈ X f ( x ) , h ( X 1 ) = h ( X 2 ) h(X) = MAX _{x \in X} f(x), h(X_1) = h(X_2) h(X)=MAXx∈Xf(x),h(X1)=h(X2) 。
该定理说明了使用Max无法区分的情况,对于Max而言:
- 既不捕获结构信息也不捕获分布信息,捕获的是 the underlying set of a multiset
- 适合识别代表性元素或 ”skeleton“ 的任务,如3D点云的骨架,并且对噪声和异常值具有鲁棒性
实验
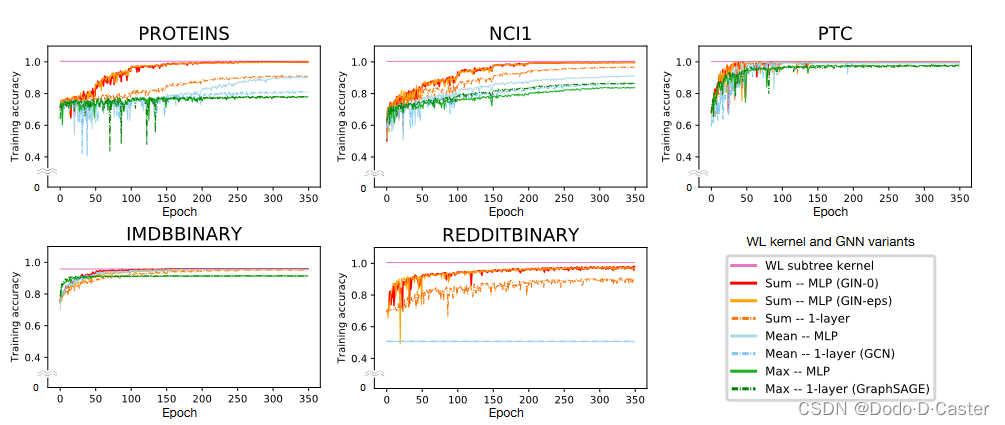
- GIN- ϵ \epsilon ϵ : 通过梯度下降法学习 ϵ \epsilon ϵ
- GIN-0 : 设置 ϵ \epsilon ϵ为固定值0

可以看出,GIN- ϵ \epsilon ϵ 和 GIN-0 对于所有数据集都有这不错的效果。此外,GIN-0 略优于 GIN- ϵ \epsilon ϵ,作者归因于其简单性。