数据结构——堆的实现

news2024/9/24 17:14:53

堆的实现-----C语言版

  • 目录：
  • 一、堆的实现
    • 1.1堆的定义
    • 1.2堆的实现
      • 1.2.1堆的各个接口
      • 1.2.2堆的向上调整
      • 1.2.3堆的向下调整
      • 1.2.4堆的定义声明和初始化
      • 1.2.5堆的数据处理
      • 1.2.6堆的判空和堆的数据个数以及堆销毁
      • 1.2.7堆的代码实现
  • 二、TOP—K问题

目录：

一、堆的实现

1.1堆的定义

堆（heap）是特殊的数据结构。堆通常是一个可以被看做一棵完全二叉树(逻辑层面上)的数组对象(物理层面上),常用来在一组变化频繁(发生增删查改的频率较高)的数据中寻找最值.将根结点最大的堆叫做最大堆或大根堆，这样可以找到堆中的最大值(根节点的值);根结点最小的堆叫做最小堆或小根堆,这样可以找到堆中的最小值。

其中堆不一定是完全二叉树，只是为了方便存储和索引，我们通常用完全二叉树的形式来表示堆而已。
二叉堆：是一个数组，它可以被看成是一个近似的完全二叉树。

最大堆，最小堆如图：
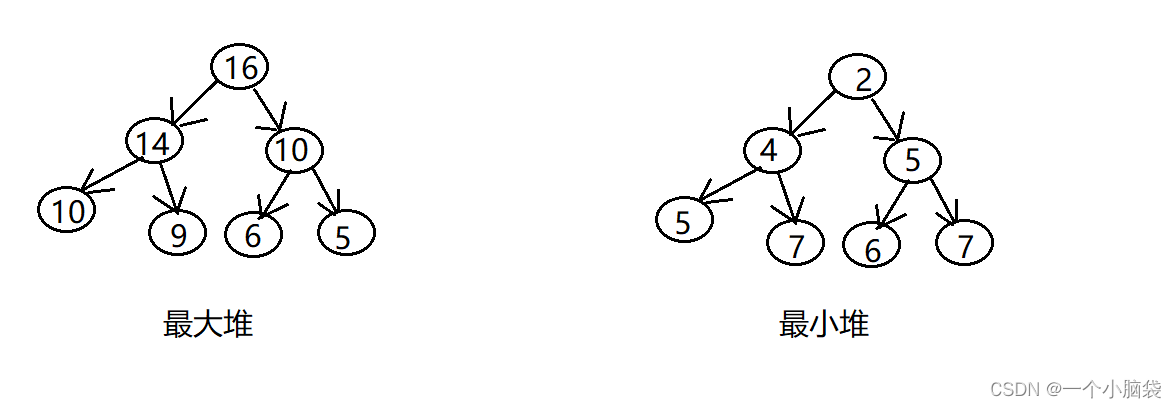
在这里插入图片描述

最大堆：根结点大于左右子树结点的值，左右子树结点的值大于它自己左右子树结点的值，一种重复下去；最小堆：根结点小于左右子树结点的值，左右子树结点的值小于它自己左右子树结点的值，一种重复下去。

1.2堆的实现

用数组实现一个堆

1.2.1堆的各个接口

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* _a;//动态数组
	int _size;//存储数据的下标
	int _capacity;//动态数组的容量
}Heap;
//堆的初始化
void HeapInit(Heap* hp);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataTypeHeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);

1.2.2堆的向上调整

//向上调整算法
void HeapJustUp(HPDataType a[], HPDataType child)
{
    int parsent;
    parsent = (child - 1) / 2;//找到孩子的父亲
    while (child > 0)
    {
        int tmp = 0;
        if (a[parsent] < a[child])//孩子比父亲的值大，
        {
            tmp = a[child];
            a[child] = a[parsent];
            a[parsent] = tmp;
        }
        else
            break;
        child = parsent;
        parsent = (parsent - 1) / 2;//找到孩子的父亲
    }
}

对于向上调整，我们把它看做是数组结构，逻辑上看做一颗完全二叉树。我们只要将要插入堆的数据通过向上调整就可以把它调整成一个大堆。向上调整算法有一个前提：除了要插入的数据，其它的数据已经构成了一个大堆，这样才能调整。

1.2.3堆的向下调整

void HeapJustDown(Heap* hp)
{
    //先假设当前待调整结点的左孩子结点存在
        //并且是待调整结点的左右孩子结点（不管右孩子结点存不存在，都这样假设）中值最大的
    int parent = 0;//根节点
    int child = parent * 2 + 1;//孩子结点
        while (child < hp->_size)
        {
            //child+1 < hp->_size说明右孩子结点确实存在
            //如果hp->_a[child] < hp->_a[child+1]也成立，那说明左右孩子结点中值最大的是右孩子结点
            if ((child + 1 < hp->_size) && hp->_a[child] < hp->_a[child + 1])
            {
                child = child + 1;
            }
            //如果a[child]>a[parent],则说明父节点比比左右孩子节点的值都要小，要置换
            if (hp->_a[child] > hp->_a[parent])
            {
                int tmp = hp->_a[parent];
                hp->_a[parent] = hp->_a[child];
                hp->_a[child] = tmp;
                parent = child;
                child = child * 2 + 1;
            }
            //如果a[child] <= a[parent],那就不需要进行调整
            else
            {
                break;
            }
        }
}

对于向下调整，我们把它看成是一个数组结构，逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个大堆。向下调整算法有一个前提：左右子树必须是一个堆，才能调整。

1.2.4堆的定义声明和初始化

1.堆的声明

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* _a;//动态数组
	int _size;//存储数据的下标
	int _capacity;//动态数组的容量
}Heap;

创建一个构成动态数组的结构体

2.堆的初始化

// 堆的初始化
void HeapInit(Heap* hp)
{
    hp->_a = (HPDataType*)malloc(sizeof(HPDataType) * 4);
    if (hp->_a == 0)
    {
        printf("malloc is error\n");
        exit(-1);
    }
    hp->_capacity = 4;
    hp->_size = 0;
}

开空间，进行初始化

1.2.5堆的数据处理

1.堆的插入

// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
    //数据满了，需要扩容
    if (hp->_capacity == hp->_size)
    {
        HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType)*hp->_capacity * 2);
        if (tmp == NULL)
        {
            printf("realloc is error");
            exit(-1);
        }
        hp->_a = tmp;
        hp->_capacity = hp->_capacity * 2;
    }
    //不需要扩容
    hp->_a[hp->_size++] = x;//插入数据，然后_size+1
    //一般数据都是放到数组尾得，建堆，向上调整，这里我们建大堆
    HeapJustUp(hp->_a, hp->_size - 1);
}

1.容量不够就扩容
2.扩容足够就插入数据
3.然后向上调整建大堆，直到满足堆

2.堆的删除

// 堆的删除，从堆顶开始删
void HeapPop(Heap* hp)
{
assert(hp);//断言为空为假的话就报错
assert(!HeapEmpty(hp));//断言如果不是空为真就执行
//首元素的的值与尾元素交换，然后删除尾元素
int tmp = hp->_a[0];
hp->_a[0] = hp->_a[hp->_size - 1];
hp->_a[hp->_size - 1] = tmp;
hp->_size--;
//堆顶元素进行向下调整
HeapJustDown(hp);
}

1.挪动覆盖删除堆顶元素，重新建堆
2.尽量保证关系不变（首尾数据交换，再删除尾部数据，向下调整建堆）

3.获取堆顶数据

// 取堆顶的数据
HPDataTypeHeapTop(Heap* hp)
{
    assert(hp->_a);
    assert(!HeapEmpty(hp));//断言如果不是空为真就执行
    return hp->_a[0];
}

堆顶数据就是第一个元素

1.2.6堆的判空和堆的数据个数以及堆销毁

1.堆的数据个数

// 堆的数据个数
int HeapSize(Heap* hp)
{
    assert(hp);
    return hp->_size;
}

堆的数据个数就是_size的个数

2.堆的判空

// 堆的判空
int HeapEmpty(Heap* hp)
{
    assert(hp);
    return hp->_size == 0;
}

_size为0，说明堆为空

3.堆销毁

// 堆的销毁
void HeapDestory(Heap* hp)
{
    assert(hp);
    free(hp->_a);
    hp->_a = NULL;
    hp->_capacity = hp->_size = 0;
}

开一块空间（malloc），程序结束之前要释放空间（free）

1.2.7堆的代码实现

.h头文件（声明）

#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* _a;//动态数组
	int _size;//存储数据的下标
	int _capacity;//动态数组的容量
}Heap;
//堆的初始化
void HeapInit(Heap* hp);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataTypeHeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);

.c源文件（定义）

#include "Heap.h"
// 堆的构建
void HeapInit(Heap* hp)
{
    hp->_a = (HPDataType*)malloc(sizeof(HPDataType) * 4);
    if (hp->_a == 0)
    {
        printf("malloc is error\n");
        exit(-1);
    }
    hp->_capacity = 4;
    hp->_size = 0;
}
//向上调整算法
HeapJustUp(HPDataType a[], HPDataType child)
{
    int parsent;
    parsent = (child - 1) / 2;//找到孩子的父亲
    while (child > 0)
    {
        int tmp = 0;
        if (a[parsent] < a[child])//孩子比父亲的值大，
        {
            tmp = a[child];
            a[child] = a[parsent];
            a[parsent] = tmp;
        }
        else
            break;
        child = parsent;
        parsent = (parsent - 1) / 2;//找到孩子的父亲
    }
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
    //数据满了，需要扩容
    if (hp->_capacity == hp->_size)
    {
        HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType)*hp->_capacity * 2);
        if (tmp == NULL)
        {
            printf("realloc is error");
            exit(-1);
        }
        hp->_a = tmp;
        hp->_capacity = hp->_capacity * 2;
    }
    //不需要扩容
    hp->_a[hp->_size++] = x;//插入数据，然后_size+1
    //一般数据都是放到数组尾得，建堆，向上调整，这里我们建大堆
    HeapJustUp(hp->_a, hp->_size - 1);
}
// 堆的判空
int HeapEmpty(Heap* hp)
{
    assert(hp);
    return hp->_size == 0;
}
//堆顶元素进行向下调整
void HeapJustDown(Heap* hp)
{
    //先假设当前待调整结点的左孩子结点存在
        //并且是待调整结点的左右孩子结点（不管右孩子结点存不存在，都这样假设）中值最大的
    int parent = 0;//根节点
    int child = parent * 2 + 1;//孩子结点
        while (child < hp->_size)
        {
            //child+1 < hp->_size说明右孩子结点确实存在
            //如果hp->_a[child] < hp->_a[child+1]也成立，那说明左右孩子结点中值最大的是右孩子结点
            if ((child + 1 < hp->_size) && hp->_a[child] < hp->_a[child + 1])
            {
                child = child + 1;
            }
            //如果a[child]>a[parent],则说明父节点比比左右孩子节点的值都要小，要置换
            if (hp->_a[child] > hp->_a[parent])
            {
                int tmp = hp->_a[parent];
                hp->_a[parent] = hp->_a[child];
                hp->_a[child] = tmp;
                parent = child;
                child = child * 2 + 1;
            }
            //如果a[child] <= a[parent],那就不需要进行调整
            else
            {
                break;
            }
        }
}
// 堆的删除，从堆顶开始删
void HeapPop(Heap* hp)
{
assert(hp);//断言为空为假的话就报错
assert(!HeapEmpty(hp));//断言如果不是空为真就执行
//首元素的的值与尾元素交换，然后删除尾元素
int tmp = hp->_a[0];
hp->_a[0] = hp->_a[hp->_size - 1];
hp->_a[hp->_size - 1] = tmp;
hp->_size--;
//堆顶元素进行向下调整
HeapJustDown(hp);
}
// 取堆顶的数据
HPDataTypeHeapTop(Heap* hp)
{
    assert(hp->_a);
    assert(!HeapEmpty(hp));//断言如果不是空为真就执行
    return hp->_a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{
    assert(hp);
    return hp->_size;
}
// 堆的销毁
void HeapDestory(Heap* hp)
{
    assert(hp);
    free(hp->_a);
    hp->_a = NULL;
    hp->_capacity = hp->_size = 0;
}

.c源文件（测试）

#include "Heap.h"
int main()
{
    Heap hp;
    HeapInit(&hp);//初始化
    HeapPush(&hp, 2);//插入数据
    HeapPush(&hp, 3);
    HeapPush(&hp, 4);
    HeapPush(&hp, 5);
    HeapPush(&hp, 6);
    HeapPush(&hp, 1);
    HeapPush(&hp, 66);
    HeapPush(&hp, 62);
    HeapPush(&hp, 4);
    HeapPush(&hp, 6);
    HeapPop(&hp);//删除数据,从堆顶开始删
   int tmp= HPDataTypeHeapTop(&hp);//取堆顶元素
    // 堆的数据个数
   int num = HeapSize(&hp);
   printf("建大堆，栈顶元素为：%d,堆的数据个数：%d\n", tmp,num);
    for (int i = 0; i < num; i++)
        printf("%d ", hp._a[i]);
    HeapDestory(&hp);// 堆的销毁
    return 0;
}

二、TOP—K问题

TOP—K问题：求数据集合中前k个最大的元素和最小的元素，一般情况数据非常大。
如：专业前10，世界500强，游戏中前100的活跃玩家，各种榜单等等。

1.用数据集合中前k个元素来建堆
求前k个最大的元素，建小堆
求前k个最小的元素，建大堆
2.用剩余的N—K个元素依次与堆顶元素来比较，根据规则替换堆顶元素，N—K个元素依次与堆顶元素比较完成后，堆里的K个元素就是所求的最小或者最大的元素。

例子：

问题：假设1亿个数，内存存不下，数据在文件中找出最大的前k个数。
1.读取文件的前10个数据，在内存数组中建立一个小堆。
2.在依次读取剩下数据，跟堆顶元素比较，大于堆顶的数据就替换它，然后向下调整。
3.所有数据读完，堆里面数据就是最大的前10个数。

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define n 100000000
void  WeinteData()//写入1亿数据
{
    
FILE* fp = fopen("top.txt", "w");//打开文件，只写
if (fp == NULL)
{
    perror("fopen error");
    exit(-1);
}
srand((unsigned)time(0));
int arr[100] = { 0 };
for (int i = 0; i < n; i++)
{
    int x = rand() % 10000 + 1;
    fprintf(fp, "%d\n", x);
}
fclose(fp);//关闭文件
}
//两个数交换
void Swap(int* p, int* q)
{
    int tmp;
    tmp = *q;
    *q = *p;
    *p = tmp;
}
//向下调整算法
void JustDown(int* arr,int k,int parent)
{
    int child = parent * 2 + 1;//左孩子结点
    while (child < k)
    {
        if ((child + 1 < k) && arr[child] > arr[child + 1])//找到最小值的孩子结点
            child += 1;
        //如果arr[child]<arr[parent],则说明父节点比比左右孩子节点的值都要大，要置换
        if (arr[child] < arr[parent])
        {
            Swap(&arr[child], &arr[parent]);
           //让孩子结点为父节点，并且更新它的儿子结点
            parent = child;
            child = child * 2 + 1;
        }
        //如果a[child] <= a[parent],那就不需要进行调整
        else
        {
            break;
        }
    }
}
//建小堆
void HeapCreate(int* arr,int k)
{
    //最后一个结点的父亲结点开始向下调整
    for (int i = (k - 2) / 2; i >= 0; --i)
    {
        //向下调整算法
        JustDown(arr, k, i);
    }
}
void  FileTakeK()
{
    int k = 10;//10个数
    int* a = (int*)malloc(sizeof(int) * k);//开辟一块空间用来建堆
    if (a == NULL)
    {
        perror("malloc error:");
        exit(-1);
    }
    FILE* file = fopen("top.txt", "r");//打开top.txt文件,只读模式
    if (file == NULL)
    {
        perror("fopen error:");
        exit(-1);
    }
    for (int i = 0; i < k; i++)
    {
        fscanf(file, "%d", &a[i]);
    }
    printf("前10个数:\n");
    for (int i = 0; i < k; i++)
        printf("%d ", a[i]);
    //建小堆
    HeapCreate(a, k);
    printf("\n建完小堆里面的数:\n");
    for (int i = 0; i < k; i++)
        printf("%d ", a[i]);
    //把剩余的n-k个数与小堆的堆顶比较，比较完成后，堆里的数就是文件里最大的10个数
    int x = 0;
    while (fscanf(file, "%d", &x) != EOF)
    {
        //比堆顶数大，把这个数赋值给堆顶，然后向下调整
        if (x > a[0])
            a[0] = x;
        JustDown(a, k, 0);
    }
    printf("\n取最大的10个数:\n");
    for (int i = 0; i < k; i++)
        printf("%d ", a[i]);
    free(a);//释放内存
    fclose(file);//关闭文件
}
int main()
{
    //写入1亿数据
   WeinteData();
       //从文件中取出k个数,建小堆
    FileTakeK();
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1248338.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

历时半年，我发布了一款习惯打卡小程序

历时半年，我发布了一款习惯打卡小程序

半年多前&#xff0c;我一直困扰于如何记录习惯打卡情况&#xff0c;在参考了市面上绝大多数的习惯培养程序后&#xff0c;终于创建并发布了这款习惯打卡小程序。 “我的小日常打卡”小程序主要提供习惯打卡和专注训练功能。致力于培养用户养成一个个好的习惯&#xff0c;改掉…
阅读更多...
[Latex] Riemann 问题中的激波，接触间断，膨胀波的 Tikz 绘图

[Latex] Riemann 问题中的激波，接触间断，膨胀波的 Tikz 绘图

Latex 代码 \begin{figure}\begin{subfigure}[b]{0.32\textwidth}\centering\resizebox{\linewidth}{!}{\begin{tikzpicture}\coordinate (o) at (0,0);\coordinate (Si) at (2.5,2.5);\coordinate (x) at (1,0);\draw[->] (0,0) -- (3,0) node[right] {$x$};\draw[->] …
阅读更多...
tp8 使用rabbitMQ（4）路由模式

tp8 使用rabbitMQ（4）路由模式

路由模式 在第三节中我们使用的 交换机的 fanout 把生产者的消息广播到了所有与它绑定的队列中处理&#xff0c;但是我们能不能把特定的消息&#xff0c;发送给指定的队列&#xff0c;而不是广播给所有队列呢&#xff1f; 如图&#xff0c;交换机把 orange 类型的消息发送给了…
阅读更多...
jQuery_02 引入jQuery，初试牛刀

jQuery_02 引入jQuery，初试牛刀

引入jquery文件 我们在官网上点击dowmload那个 会发现进入了一个网页&#xff0c;里面全部是代码&#xff0c;你可能还在想为什么下载不了&#xff0c;其实jquery不跟vue一样&#xff0c;整个jquery就是一个js文件而已&#xff0c;所以直接ctrla 全选 ctrlc复制 &#xff0c;然…
阅读更多...
关于爱普生L3219彩色喷墨打印机打印过程中噪声过大的几点缓解方法

关于爱普生L3219彩色喷墨打印机打印过程中噪声过大的几点缓解方法

故障描述&#xff1a; 一台新购买的爱普生L3219使用过程中出现了噪声过大的问题&#xff0c;每次打印或者复印都或有明显的噪音过大的现象&#xff0c;目测观察大概是打印机字车左右来回移动的时候剐蹭滑道的问题&#xff0c;与经销商沟通后由经销商联系上级供货商更换一台全新…
阅读更多...
elk 简单操作手册

elk 简单操作手册

1.1. 基础概念 EFK不是一个软件,而是一套解决方案,开源软件之间的互相配合使用,高效的满足了很多场合的应用,是目前主流的一种日志系统。 EFK是三个开源软件的缩写,分别表示:Elasticsearch , Filebeat, Kibana , 其中Elasticsearch负责日志保存和搜索,Filebeat负责收集日志,Ki…
阅读更多...
喜报｜AIRLOOK荣获“创客北京2023”创新创业大赛企业组三等奖

喜报｜AIRLOOK荣获“创客北京2023”创新创业大赛企业组三等奖

“创客北京2023”创新创业总决赛圆满落幕&#xff0c;埃洛克航空科技&#xff08;北京&#xff09;有限公司&#xff0c;&#xff08;以下统称AIRLOOK&#xff09;首次参赛即从几千家企业中脱颖而出&#xff0c;荣获大赛企业组三等奖。 自2016年开始&#xff0c;“创客北京”大…
阅读更多...
JMeter---BeanShell实现接口前置和后置操作

JMeter---BeanShell实现接口前置和后置操作

在JMeter中&#xff0c;可以使用BeanShell脚本来实现接口的前置和后置操作。 下面是使用BeanShell脚本实现接口前置和后置操作的步骤&#xff1a; 1、在测试计划中添加一个BeanShell前置处理器或后置处理器。 右键点击需要添加前置或后置操作的接口请求&#xff0c;选择&quo…
阅读更多...
C# ReadOnlyRef Out

C# ReadOnlyRef Out

C# ReadOnly ReadOnly先看两种情况1.值类型2.引用类型 结论 Ref Out ReadOnly官方文档 ReadOnly 先看两种情况 1.值类型 当数据是值类型时&#xff0c;标记为Readonly时&#xff0c;如果再次设置值&#xff0c;会提示报错&#xff0c;无法分配到只读字段 public class A {pri…
阅读更多...
计算机组成原理。3-408

计算机组成原理。3-408

1.动态存储和静态存储 2.双端口RAM 注意&#xff1a;cpu通过地址线和数据线读写数据时&#xff0c;不能同时写&#xff0c;但可以同时读&#xff0c;也不能一边读一边写。 3.多体并行存储器 分为高位存储和低位存储 小结 4.磁盘存储器的组成 5.磁盘的性能指标 磁盘读写寻道…
阅读更多...
vcsa6.7打补丁操作

vcsa6.7打补丁操作

首先到官网中查找到最新的patch&#xff0c;需要有注册账号才可操作 网址链接&#xff1a;https://customerconnect.vmware.com/patch#search 下载后把iso文件上传到磁盘中&#xff0c;vcsa虚拟机中做光盘iso挂接后&#xff0c; 使用浏览器输入https://ip:5480登录&#xff…
阅读更多...
220v转5V/150MA电源芯片专业替代阻容降压

220v转5V/150MA电源芯片专业替代阻容降压

标题&#xff1a;220V转5V/150MA电源芯片专业替代阻容降压&#xff0c;SOT23-3小封装&#xff0c;内置高压MOS管&#xff0c;45V-265V输入&#xff0c;固定5V输出&#xff0c;峰值电流200ma&#xff0c;逐周期限流、输出短路保护&#xff0c;片上过温保护&#xff08;OTP&#…
阅读更多...
最新AI创作系统ChatGPT系统运营源码，支持GPT-4图片对话能力，上传图片并识图理解对话,支持DALL-E3文生图

最新AI创作系统ChatGPT系统运营源码，支持GPT-4图片对话能力，上传图片并识图理解对话,支持DALL-E3文生图

一、AI创作系统 SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI创作ChatGPT&#xff1f;小编这里写一个详细图文教程吧&#xff01;本系统使用NestjsVueTypescript框架技术&#xff0c;持续集成AI能力到本系统。支持OpenAI DALL-E3文生图&#xff0c;…
阅读更多...
js粒子效果(一)

js粒子效果(一)

效果: 代码: <!doctype html> <html> <head><meta charset"utf-8"><title>HTML5鼠标经过粒子散开动画特效</title><style>html, body {position: absolute;overflow: hidden;margin: 0;padding: 0;width: 100%;height: 1…
阅读更多...
Edit And Resend测试接口工具（浏览器上的Postman）

Edit And Resend测试接口工具（浏览器上的Postman）

优点 可以不用设置Cookie或者Token&#xff0c;只设置参数进行重发接口测试API 使用Microsoft Rdge浏览器 F12——然后点击网络——在页面点击发起请求——然后选择要重发的请求右键选择Edit And Resend——在网络控制台设置自己要设置的参数去测试自己写的功能
阅读更多...
【C++初阶】STL之学习string的用法

【C++初阶】STL之学习string的用法

目录 前言&#xff1a;一、认识下string1.1 什么是string1.2 为什么要有string 二、string 类的接口使用2.1 初始化与析构2.1.1 初始化2.1.2 析构 2.2 容量操作2.2.1 长度大小——size和length2.2.2 空间总大小——capacity2.2.3 判空——empty2.2.4 清空——clear2.2.5 预留空…
阅读更多...
使用v-md-editor开发sql查看器--实战

使用v-md-editor开发sql查看器--实战

v-md-editor markdown编辑器 文档&#xff1a;https://code-farmer-i.github.io/vue-markdown-editor/zh/ echo 创建一个空目录&#xff0c;使用vscode打开此空目录&#xff0c;进入终端&#xff0c;输入如下命令 npm create vitelatest . -- --template vue echo 选择 vue 和 …
阅读更多...
Linux：gdb调试器的解析+使用(超详细版)

Linux：gdb调试器的解析+使用(超详细版)

Linux调试器-gdb 背景&#xff1a; 程序的发布方式有两种&#xff0c;debug模式和release模式 debug模式&#xff1a;可以被调试&#xff1b; release模式&#xff1a;不可以被调试。 为什么需要debuy和release这两个模式呢&#xff1f; 答&#xff1a;程序员在开发的时候需要…
阅读更多...
git提交报错error: failed to push some refs to ‘git url‘

git提交报错error: failed to push some refs to ‘git url‘

1.产生错误原因 想把本地仓库提交到远程仓库&#xff0c;报错信息如下 git提交报错信息 error: src refspec master does not match any error: failed to push some refs to git url 错误原因&#xff1a; 我们在创建仓库的时候&#xff0c;都会勾选“使用Reamdme文件初始化…
阅读更多...
论文导读 | 10月专题内容精选：人的预测

论文导读 | 10月专题内容精选：人的预测

编者按 本次论文导读&#xff0c;编者选择了10月份OR和MS上与"人的预测"有关的三篇文章&#xff0c;分别涉及群体智慧的提取&#xff0c;个体序列预测的评估&#xff0c;以及决策者对风险的扭曲感知在分布式鲁棒优化中的应用。其中&#xff0c;从基于"生成式可能…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023