每日一题(LeetCode)----链表–链表最大孪生和
1.题目(2130. 链表最大孪生和)
-
在一个大小为
n且n为 偶数 的链表中,对于0 <= i <= (n / 2) - 1的i,第i个节点(下标从 0 开始)的孪生节点为第(n-1-i)个节点 。- 比方说,
n = 4那么节点0是节点3的孪生节点,节点1是节点2的孪生节点。这是长度为n = 4的链表中所有的孪生节点。
孪生和 定义为一个节点和它孪生节点两者值之和。
给你一个长度为偶数的链表的头节点
head,请你返回链表的 最大孪生和 。示例 1:
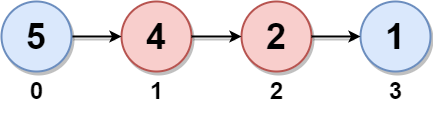
输入:head = [5,4,2,1] 输出:6 解释: 节点 0 和节点 1 分别是节点 3 和 2 的孪生节点。孪生和都为 6 。 链表中没有其他孪生节点。 所以,链表的最大孪生和是 6 。示例 2:
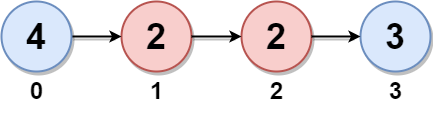
输入:head = [4,2,2,3] 输出:7 解释: 链表中的孪生节点为: - 节点 0 是节点 3 的孪生节点,孪生和为 4 + 3 = 7 。 - 节点 1 是节点 2 的孪生节点,孪生和为 2 + 2 = 4 。 所以,最大孪生和为 max(7, 4) = 7 。示例 3:
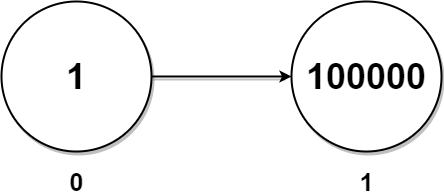
输入:head = [1,100000] 输出:100001 解释: 链表中只有一对孪生节点,孪生和为 1 + 100000 = 100001 。提示:
- 链表的节点数目是
[2, 105]中的 偶数 。 1 <= Node.val <= 105
- 比方说,
2.解题思路
思路一
将链表的后一半进行反转,然后将链表的前一半和后一半进行相加,通过比较得到结果
1.找到链表的后一半的起始节点
我们先计算出整个链表的长度,然后用一个指针指向链表表头,向后走整个链表的一半长度,得到链表后一半的表头
2.进行反转
通过头,拿,断这三个指针实现反转
3.定义一个存结果的变量,将反转后的后一半链表与原链表的前一半进行相加(这里思路一和思路二实现方式不一样,但是都差不多),然后每求出一个值,就和存结果的变量进行比较,如果大于,就把存结果的变量进行更新,如果不大于,就不进行更新
思路二:思路二和思路一一样就是实现的方法不同
1.找到链表的后一半的起始节点
我们使用快慢指针找出后一半部分的起始节点。我们用慢指针和快指针同时指向 头节点,然后,我们每次将慢指针向后移动一个节点,同时快指针向后移动两个节点。当 快指针指向空结点时,慢指针就刚好指向链表了后一半部分的首节点
2.进行反转
通过头,拿,断这三个指针实现反转
3.定义一个存结果的变量,将反转后的后一半链表与原链表的前一半进行相加(这里思路一和思路二实现方式不一样,但是都差不多),然后每求出一个值,就和存结果的变量进行比较,如果大于,就把存结果的变量进行更新,如果不大于,就不进行更新
3.写出代码
思路一的代码
class Solution {
public:
int pairSum(ListNode* head) {
int length1=0;
ListNode* Temp=head;
while(Temp){
length1++;
Temp=Temp->next;
}
int length2=length1/2;
int t=length2;
Temp=head;
while(t--){
Temp=Temp->next;
}
ListNode* head2=NULL;
ListNode* na=Temp;
ListNode* duan=Temp->next;
while(duan){
na->next=head2;
head2=na;
na=duan;
duan=duan->next;
}
na->next=head2;
head2=na;
int res=-1;
for(int i=0;i<length2;i++){
res=max(head->val+head2->val,res);
head=head->next;
head2=head2->next;
}
return res;
}
};
思路二的代码
class Solution {
public:
int pairSum(ListNode* head) {
ListNode* fast=head;
ListNode* slow=head;
while(fast){
slow=slow->next;
fast=fast->next->next;
}
ListNode* head2=NULL;
ListNode* na=slow;
ListNode* duan=slow->next;
while(duan){
na->next=head2;
head2=na;
na=duan;
duan=duan->next;
}
na->next=head2;
head2=na;
int res=-1;
while(head2){
res=max(head->val+head2->val,res);
head2=head2->next;
head=head->next;
}
return res;
}
};