目录
前言
一、问题引入
二、一个例子
1.生成散点图
2.对数据进行剖分
3.点法式分析
三、最后结果
前言
上一篇文章感觉对三角剖分问题没有说清楚,这次专门对三角剖分问题再仔细说说。
一、问题引入
实际上这个问题是用来解决二维曲面插值问题的。
二维插值问题,用matlab的一些函数就可以方便操作,比如 interp2 。但 interp2函数是用在规则点数据集的情况下,比如已知“密度较稀疏”的一些数据点,进行插值,找到“密度适中”的点。下面举个例子说明。
% 生成自定义的网格点
x = linspace(-3, 3, 10);
y = linspace(-3, 3, 15);
[X, Y] = meshgrid(x, y);
% 计算相应的高度值
Z = peaks(X, Y);
% 绘制原始网格图
figure;
subplot(1, 2, 1);
surf(X, Y, Z);
xlabel('X');
ylabel('Y');
zlabel('Z');
title('Original Peaks Surface');
axis tight;
grid on;
% 指定插值后的网格点
xi = linspace(-3, 3, 30);
yi = linspace(-3, 3, 45);
[XI, YI] = meshgrid(xi, yi);
% 使用插值方法计算插值后的高度值
ZI = interp2(X, Y, Z, XI, YI, 'spline');
% 绘制插值后的网格图
subplot(1, 2, 2);
surf(XI, YI, ZI);
xlabel('X');
ylabel('Y');
zlabel('Z');
title('Interpolated Peaks Surface');
axis tight;
grid on;得到图如下:
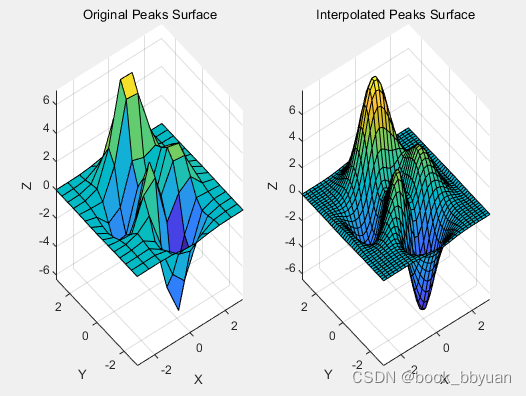
但对于一些无序(或者说在空间排列没有规律)的散点进行插值,这时要使用 三角剖分插值
具体概念介绍可以参考下面的wiki链接
https://en.wikipedia.org/wiki/Delauna4_triangulation
二、一个例子
1.生成散点图
为了好说明,我们在1/4半球面上进行操作,随机选取球面上的一些点作为散点,同时画出它的xy面投影剖分(后面要用)
% 定义半径和绘制分辨率
radius = 1; % 半径
resolution = 50; % 分辨率
% 生成球面上的坐标点
theta = linspace(-pi/2, 0, resolution);
phi = linspace(0, pi/2, resolution);
[THETA, PHI] = meshgrid(theta, phi);
x = radius * sin(PHI) .* cos(THETA);
y = radius * sin(PHI) .* sin(THETA);
z = radius * cos(PHI);
% 随机选择50个点
numPoints = 50;
indices = randperm(resolution^2, numPoints);
selectedPoints = [x(indices(:)), y(indices(:)), z(indices(:))];
% 进行三角剖分
tri = delaunay(selectedPoints(:, 1), selectedPoints(:, 2));
% 绘制1/4半球面
figure;
surf(x, y, z);
hold on;
% 绘制随机选择的点
scatter3(selectedPoints(:, 1), selectedPoints(:, 2), selectedPoints(:, 3), 'filled', 'r'); 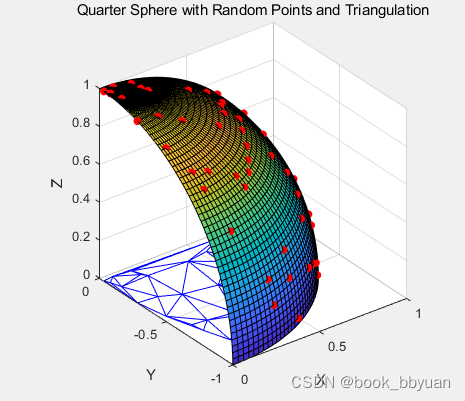
2.对数据进行剖分
代码如下:
clear all
close all
clc
rng(10)
% 定义半径和绘制分辨率
radius = 1; % 半径
resolution = 50; % 分辨率
% 生成球面上的坐标点
theta = linspace(-pi/2, 0, resolution);
phi = linspace(0, pi/2, resolution);
[THETA, PHI] = meshgrid(theta, phi);
x = radius * sin(PHI) .* cos(THETA);
y = radius * sin(PHI) .* sin(THETA);
z = radius * cos(PHI);
% 随机选择点
numPoints = 50;
indices = randperm(resolution^2, numPoints);
selectedPoints = [x(indices(:)), y(indices(:)), z(indices(:))];
save selectedPoints.mat selectedPoints
% 在xy平面上进行平面剖分
dt = delaunayTriangulation(selectedPoints(:, 1), selectedPoints(:, 2));
tri = dt.ConnectivityList;
% 根据剖分点的坐标和对应的z值生成三维空间中的三角网格
tri3D = [tri, tri(:, 1) + size(selectedPoints, 1), tri(:, 2) + size(selectedPoints, 1)];
x3D = [selectedPoints(:, 1); selectedPoints(:, 1); selectedPoints(:, 1)];
y3D = [selectedPoints(:, 2); selectedPoints(:, 2); selectedPoints(:, 2)];
z3D = [selectedPoints(:, 3); selectedPoints(:, 3); selectedPoints(:, 3)];
% 绘制1/4半球面
figure;
h = surf(x, y, z);
set(h, 'FaceAlpha', 0.5); % 设置表面的透明度
% set(h, 'FaceColor', 'green'); % 设置表面颜色为空
hold on;
% 绘制随机选择的点
scatter3(selectedPoints(:, 1), selectedPoints(:, 2), selectedPoints(:, 3), 'filled', 'r');
triplot(dt);
% % 绘制三角网格
% trisurf(tri3D, x3D, y3D, z3D, 'FaceColor', 'none', 'EdgeColor', 'b', 'FaceAlpha', 0.5);
% 绘制三角网格
patch('Faces', tri3D, 'Vertices', [x3D, y3D, z3D], 'FaceColor', 'red', 'EdgeColor', 'b', 'FaceAlpha', 0.5);
% 设置坐标轴和标题
xlabel('X');
ylabel('Y');
zlabel('Z');
title('Quarter Sphere with Random Points and Triangulation');
% 设置坐标轴比例和网格
axis equal;
grid on;
这个显示的有点复杂了,它是几个数据图像的结合 包括 原始数据(网格图)、散点图(红色)、空间和平面三角剖分图(蓝色)

我们去掉原始网格图,只留平面剖分和对应曲面的映射,看看如下
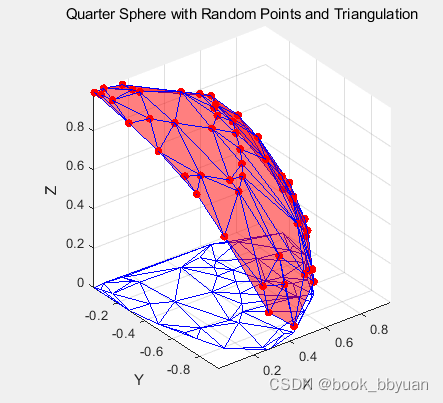
待插值的点会在这些红色三角面上找到对应的z值,因为散点插值可不同于interp2插值,根本没有"可以依赖"现成附近的方形网格点用来估算,需要借助剖分的找到它附近的点。好了,思路有了,流程化的东西如下:
三角剖分的流程
1、对空间散点的xy平面投影进行三角剖分(注意:并不是直接在空间曲面上进行三角剖分,而是对平面进行,因为使用delaunayTriangulation会对xyz三维数据直接给出的四面体立体剖分!即它会认为是立体剖分)
2、对待插值点的xy平面投影点,找到它属于xy平面剖分的哪个三角形(注意,是在xy平面)
3、在空间对对应三角形建立平面方程,然后使用点法式方式对待插值点求出z的值
平面和立体对应关系如下图(共同的xy,z当然不同了)
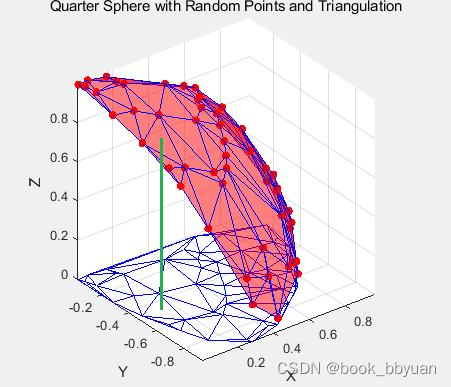
3.点法式分析
参考代码,还是沿用上一次提到的线性三角剖分的matlab代码
https://www.mathworks.com/matlabcentral/fileexchange/38925-linearly-interpolate-triangulation

这代码核心的部分在这里:

其中点法式大家估计印象不是很深刻了,需要复习下空间解析几何的一点知识 ,两页ppt帮大家回疑

法向量怎么求呢,相当于在平面中两个矢量的叉乘!我们翻一下matlab cross的内容
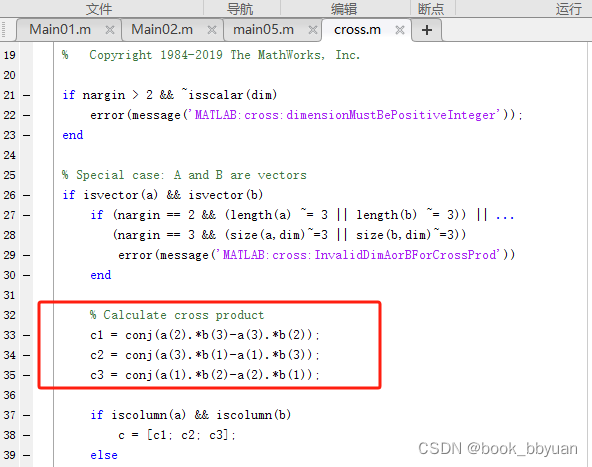
比如两个矢量 V1 = [x2-x1,y2-y1,z2-z1],V2=[x3-x1,y3-y1,z3-z1],,记为 (a1,a2,a3) (b1,b2,b3)
叉乘的结果是
A=a2*b3 - a3*b2=(y2-y1)*(z3-z1)-(z2-z1)*(y3-y1)
B = a3*b1-a1*b3=(z2-z1)*(x3-x1)-(x2-x1)*(z3-z1)
C = a1*b2-a2*b1 = (x2-x1)*(y3-y1)-(y2-y1)*(x3-x1)
A*(xi-x1)+B*(yi-y1)+C*(zi-z1) = 0
zi = (-((y3 - y1) * (z2 - z1) - (z3 - z1) * (y2 - y1)) * (x - x1) - ((z3 - z1) * (x2 - x1) - (x3 - x1) * (z2 - z1)) * (y - y1)) / ((x3 - x1) * (y2 - y1) - (y3 - y1) * (x2 - x1)) + z1
z1变到分子上去,然后分子变成 z1*XXX+z2*YYY+z3*CCC ,XXX,YYY,CCC就是代码中N1 N2 N3的分子
这样按照待插值的网格的点的顺序,依次计算即可得到全部的插值数据。
三、最后结果
简单对几个点进行插值,插值之后的空间点是黄色:
load selectedPoints.mat
%散点
x = selectedPoints(:,1);
y = selectedPoints(:,2);
z = selectedPoints(:,3);
% 定义插值点的网格
n_points = 5; % 插值点个数
xi = linspace(min(x), max(x), n_points); % x 坐标范围
yi = linspace(min(y), max(y), n_points); % y 坐标范围
[XI, YI] = meshgrid(xi, yi); % 插值点的网格
%x y z数据同前
% 构建三角剖分
DT = delaunayTriangulation(x, y);
% Get the connectivity table
tri = DT.ConnectivityList;
tri = tri(:, [1, 2, 3]);
ZI=interptri(tri,x,y,z,XI,YI);
% 绘制插值结果
figure(1)
hold on
% surf(XI, YI, ZI);
scatter3(XI(:), YI(:), ZI(:), 'filled', 'y');
xlabel('X');
ylabel('Y');
zlabel('Z');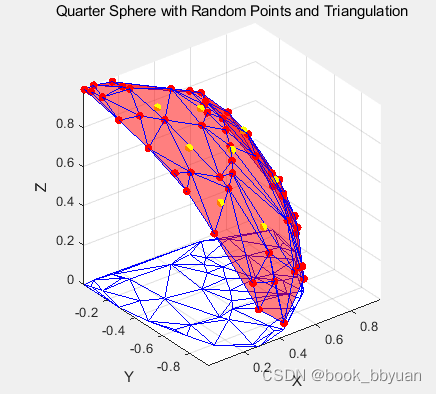
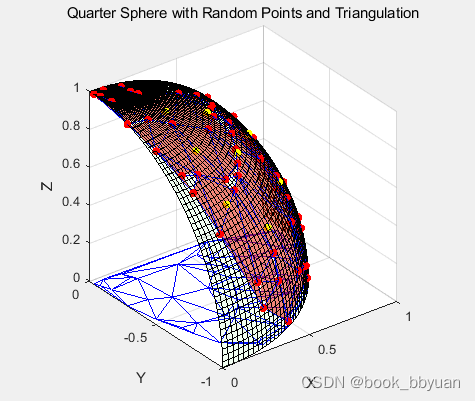
很显然,原始插值点密集的话,插出来的曲面会更理想。
总结:空间曲面散点的三角剖分线性插值是一种常用的方法,用于从离散的散点数据中构建连续的曲面模型。该方法基于三角剖分技术,将散点分布的空间曲面划分为一系列三角形,然后利用线性插值来估计每个三角形内部的数据点。