算法复杂度分为时间复杂度和空间复杂度

• 时间复杂度是指执行这个算法所需要的计算工作量
• 空间复杂度是指这个算法所需要的内存空间

1.对于一个循环，假设循环体的时间复杂度为O(n),循环次数为n，则这个循环的时间复杂度为O(n*1)。

void aFunc(int n) {
    for(int i = 0; i < n; i++) {         // 循环次数为 n
        printf("Hello, World!\n");      // 循环体时间复杂度为 O(1)
    }
}

此时时间复杂度为O(n*1),即O(n)

2.对于多个循环，假设循环体的时间复杂度为O(n)，分析的时候应该由内向外分析这些循环。

void aFunc(int n) {
    for(int i = 0; i < n; i++) {         // 循环次数为 n
        for(int j = 0; j < n; j++) {       // 循环次数为 n
            printf("Hello, World!\n");      // 循环体时间复杂度为 O(1)
        }
    }
}

此时时间复杂度为O(nn1)，即O(n^2)。

3.对于顺序执行的语句或者算法，总的时间复杂度等于其中最大的时间复杂度

void aFunc(int n) {
    // 第一部分时间复杂度为 O(n^2)
    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            printf("Hello, World!\n");
        }
    }
    // 第二部分时间复杂度为 O(n)
    for(int j = 0; j < n; j++) {
        printf("Hello, World!\n");
    }
}

此时时间复杂度为 max(O(n^2), O(n))，即 O(n^2)。

4.对于条件判断语句，总的时间复杂度等于其中 时间复杂度最大的路径 的时间复杂度。

void aFunc(int n) {
    if (n >= 0) {
        // 第一条路径时间复杂度为 O(n^2)
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < n; j++) {
                printf("输入数据大于等于零\n");
            }
        }
    } else {
        // 第二条路径时间复杂度为 O(n)
        for(int j = 0; j < n; j++) {
            printf("输入数据小于零\n");
        }
    }
}

此时时间复杂度为 max(O(n^2), O(n))，即 O(n^2)。

时间复杂度分析的基本策略是：从内向外分析，从最深层开始分析。如果遇到函数的调用，要深入函数进行分析

o(1), o(n), o(logn), o(nlogn)不仅仅用于表示时间复杂度，也用于表示空间复杂度。

O(1), O(n), O(logn), O(nlogn) 的区别：
O后面的括号中有一个函数，指明某个算法的耗时/耗空间与数据长量之间的关系。其中n代表输入数据的量。

1.O(1)就是最低的时空复杂度了，也就是耗时/耗空间与输入数据大小无关，无论输入数据增大多少倍，耗时/耗空间都不变。哈希算法就是典型的0(1)时间复杂度，无论数据规模多大，都可以在一次计算后找到目标(不考虑冲突的话)

2.时间复杂度为0(n),就是代表数据量增大几倍，耗时也增大几倍。比如常见的遍历算法。

3.O(logn)，当数据增大n倍时，耗时增大logn倍，（这里log是以2为底的，比如，当数据增大256倍时，耗时增大8倍，是比线性还要低的时间复杂度）。二分查找就是O(logn)的算法，每找一次排除一半的可能，256个数据中只要找8次就可以找到目标。

4.O(nlogn)同理，就是n乘以logn，当数据增大256倍时，耗时增大256*8=2048倍。这个复杂度高于线性低于平方。归并排序就是O(nlogn)的时间复杂度。

时间复杂度大小比较:

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n)

数据结构操作的复杂性

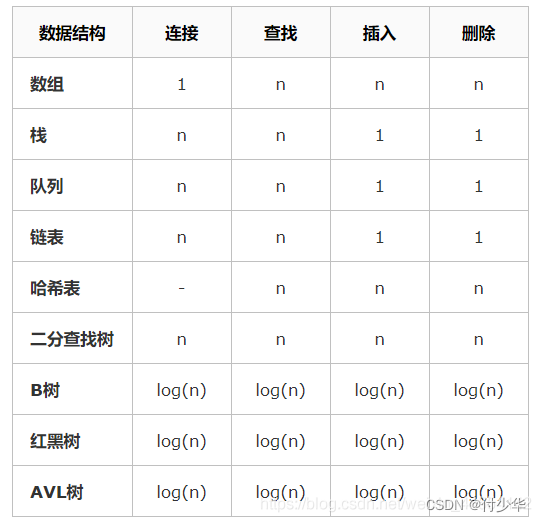
数组排序算法的复杂性