今天AC了一道题(后面的题目对我来说好难,刷不动了)
P2895 [USACO08FEB]Meteor Shower S
P2895 [USACO08FEB]Meteor Shower S_lxh0113的博客-CSDN博客
学的新知识:
dijkstra算法
dijkstra算法是求最短路径的算法。相比较于floyd算法,这个的时间复杂度更小。
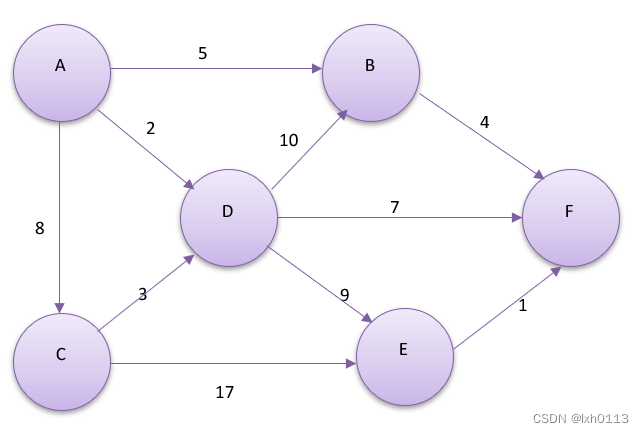
我们以下图为例子:找出从A点到其余各点的最短距离。
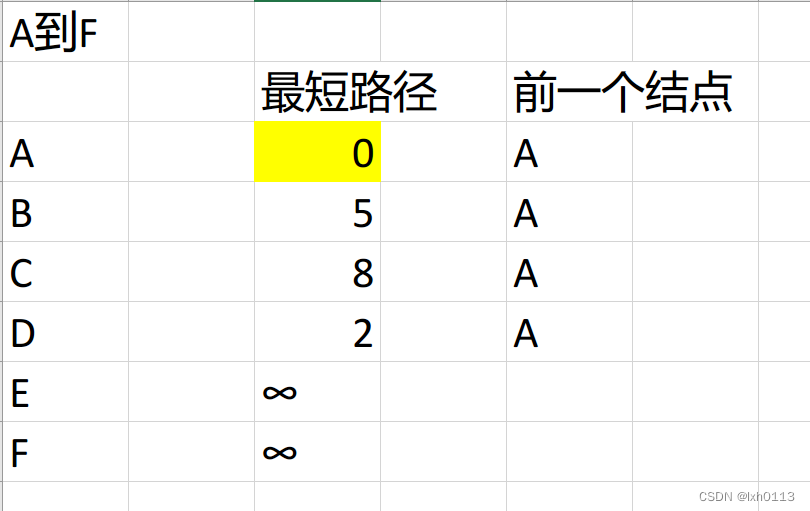
先得到这张表:

从A点到A点我们最短路径为0,所以刷新A点最短路径。为0.
从A点可以去B点和C、D点,都比所对应的无穷要小,所以先刷新,加上刷新前节点。
从A点延生是B,C,D点,找到最小的路径,是D点. 所以我们从D点延生,先确定D点已经是最佳路径,从D点能去B,E,F点。
我们发现从D点到的B点的值是12,比B存储的值是要大的,所以我们不刷新它。从D点到F点是2+7=9,所以我们刷新F点的最短路径是9。从D点到E点是2+9=11,所以E点是11.如下图所示
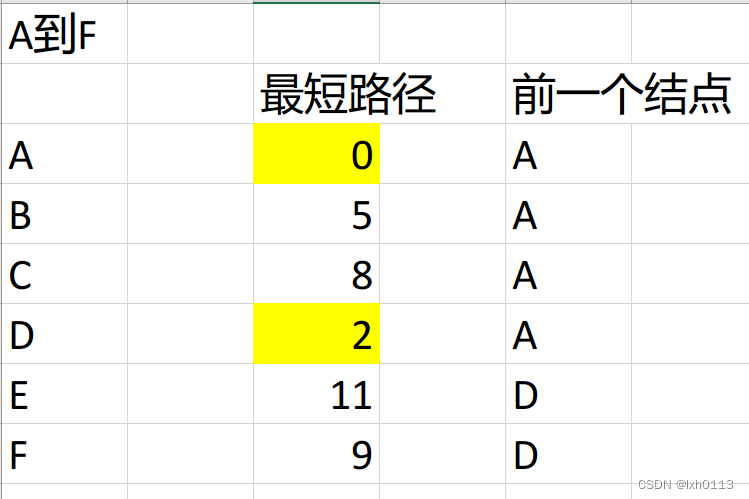
黄色代表是已经确立的最短路径,然后从剩下的里面选择最短的数字,是B点,把它变黄,我们从B点延生,B只能去F点,B点到F点是5+4=9,相同,那我们可以不用刷新它。
我们每次都从剩下的里面找最短的,确立它,然后从它延生看接下来能到哪里,如果小于当前的值,我们就刷新它,最后我们会得到一个A到其他点都是最短路径的结果。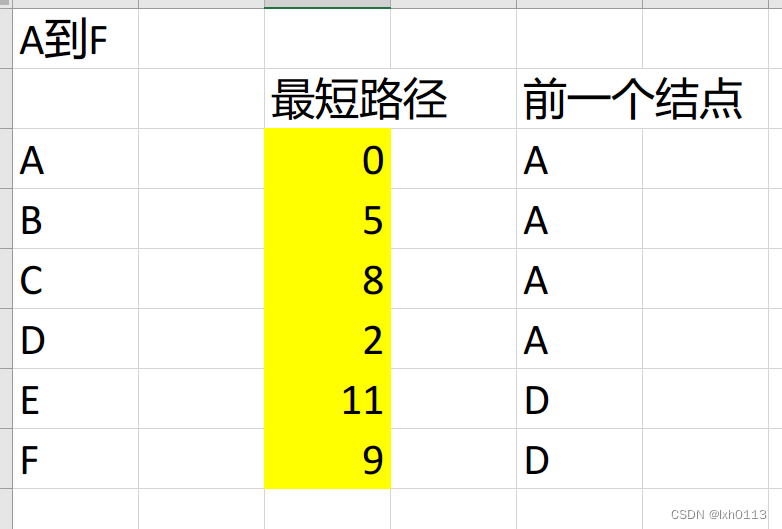
揭秘为什么要记住前一个结点,我们可以从这里找到路径。
打一个比方如果我们要找A到F点的最短路径节点,那么找到F点,F点所记录的前驱节点是D,我们找到D,D的前节点是A,所以找到了
Bellman-Ford算法

Dijkstra算法是很好,都是不能解决路径为负值的情况。所以就有了Bellman-Ford算法,它能解决这个问题。
因为如果出现负数,那么每次转一次圈都会使最小路径刷新,就没有最短路径。
我们把这个表变成下面这样 (因为这个是无向图,就是没有方向的图,所以需要全部列完)

这个算法的思路是:
1.我们需要外循坏遍历n个节点-1次,因为最多需要遍历n-1次就能得到最优解。内循环是遍历所有的边。
2.我们需要遍历每条边,找到边的终点所对应的min数组(这是存储最小路径的数组)的值,看这个值是否比访问的节点u[i[加上该访问节点到终点节点的路径也就是w[i],代码是
if(min[v[i]]>min[u[i]]+w[i])
min[v[i]]=min[u[i]]+w[i];
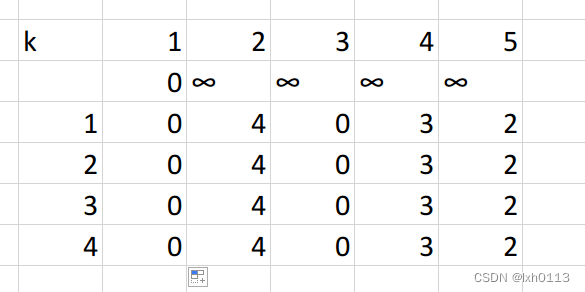
3.从上面不难看出,在k=1时,就已经得出了最小路径,(这个例子没取好),如果存在负环路时,每次外循坏都会使min数组变小。而变小是没有截止的。所以我们最多需要n-1次外循坏即可。
4.我们因为每条边都会遍历,所以我们会慢慢的得到最短路径。
5.需要注意的是min数组需要赋初值,都要赋值成最大(我这里写的是9999999),第一个除外,因为第一个顶点到自己永远是0,所以是确立的。
所以代码是:
#include<stdio.h>
#define N 100
#define MAX 999999
int u[N],v[N],w[N],min[N];
int bellman(int n,int m)
{
int i,j;
for(i=1;i<n;i++)
{
for(j=1;j<=m;j++)
{
if(min[v[i]]>min[u[i]]+w[i])
min[v[i]]=min[u[i]]+w[i];
}
}
}
int main()
{
int n,m,i;
puts("请输入你所要的顶点:");
scanf("%d",&n);
for(i=2;i<=n;i++)
{
min[i]=MAX;
}
puts("请输入边的总数:");
scanf("%d",&m);
puts("请输入各顶点与终点和边长:");
for(i=1;i<=m;i++)
{
scanf("%d%d%d",&u[i],&v[i],&w[i]);
}
bellman(n,m);
for(i=1;i<=n;i++)
{
printf("1-%d is %d\n",i,min[i]);
}
return 0;
}最后答案是: