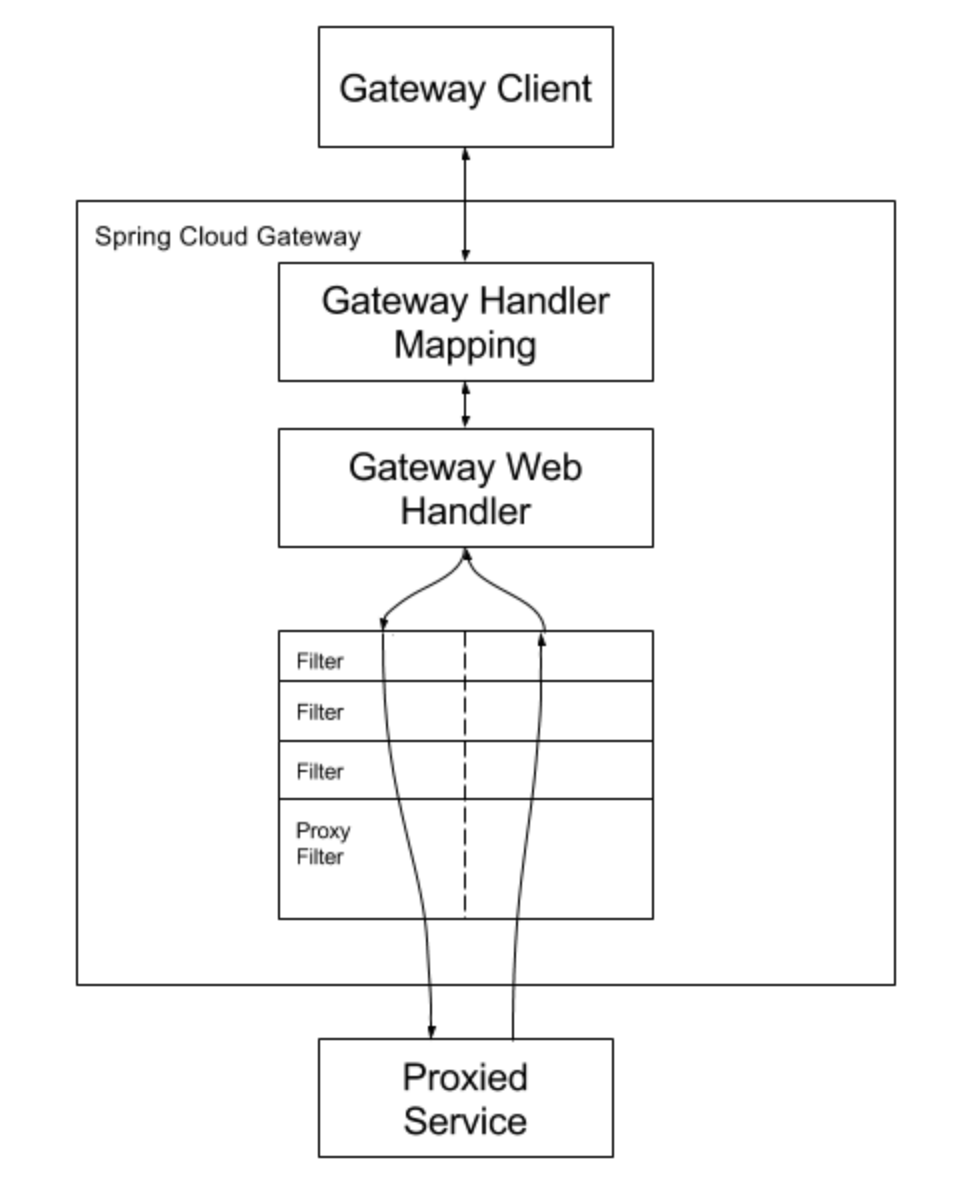
拟合的结果是得到一个确定的曲线
最小二乘法的几何解释:

argmin 存在参数k,b使括号里的值最小
第一种有绝对值,不易求导(求导在求最小值),计算较为复杂;所以我们往往使用第二种定义,也正是最小二乘的思想。
为什么不用四次方?
(1)避免极端数据对拟合曲线的影响。
(2)最小二乘法得到的结果和MLE极大似然估计一致。
不用奇数次方的原因:误差会正负相抵
求解最小二乘法:

MATLAB代码:
load data1
plot(x,y,'o')
% 给x和y轴加上标签
xlabel('x的值')
ylabel('y的值')
n = size(x,1);
k = (nsum(x.y)-sum(x)sum(y))/(nsum(x.x)-sum(x)sum(x))
b = (sum(x.x)sum(y)-sum(x)sum(x.y))/(nsum(x.x)-sum(x)*sum(x))如何评价拟合的好坏:

SSE越小越好
思考:y=a+bx*x是线性函数吗?
答:是的,因为我们这里说的线性函数是指对参数为线性(线性于参数)
如何判断线性于参数的函数?
在函数中,参数仅以一次方出现,且不能乘以或除以其他任何的参数,并不
能出现参数的复合函数形式。(二次、指数、三次函数是)
计算拟合优度的代码:
y_hat = k*x+b; % y的拟合值
SSR = sum((y_hat-mean(y)).^2) % 回归平方和
SSE = sum((y_hat-y).^2) % 误差平方和
SST = sum((y-mean(y)).^2) % 总体平方和
SST-SSE-SSR
R_2 = SSR / SST注:mean()是求均值的函数
拟合工具箱:cftool
分享:
“须知少时凌云志 曾许人间第一流”