A*算法原理
全局路径规划算法,根据给定的起点和终点在全局地图上进行总体路径规划。
导航中使用A*算法计算出机器人到目标位置的最优路线,一般作为规划的参考路线
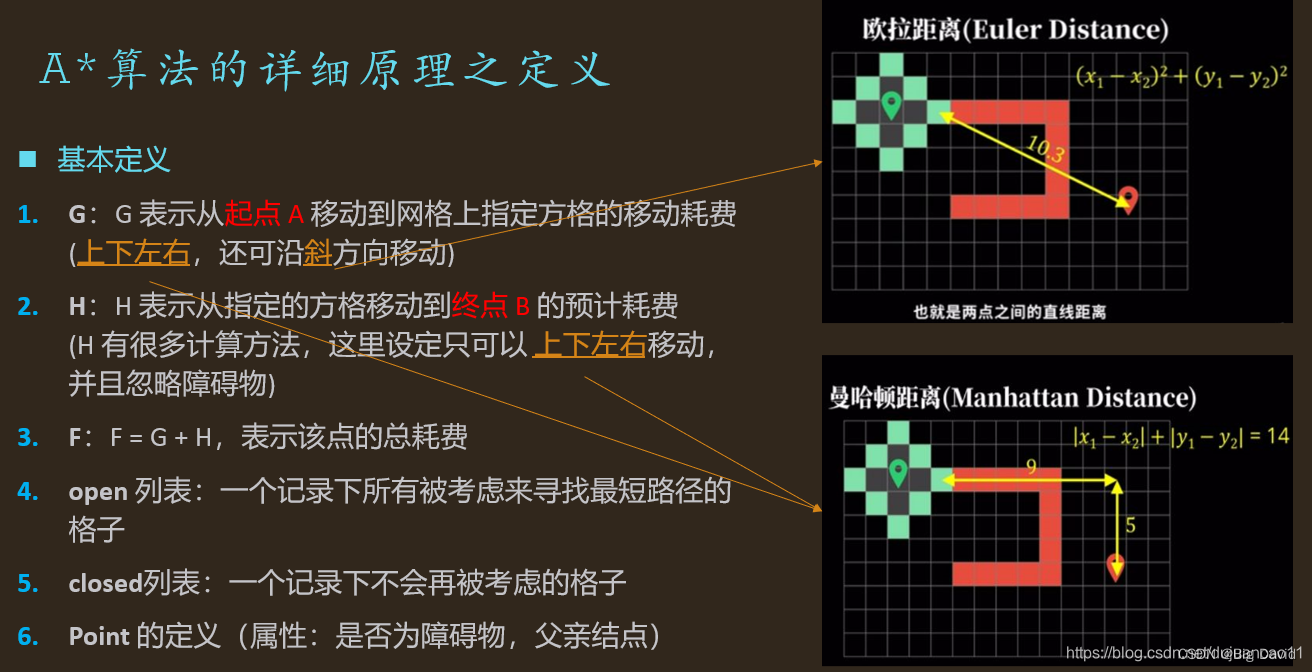
// 定义地图上的点
struct Point
{
int x,y; // 栅格行列
Point(int x, int y):x(x),y(y){}; // 参数列表初始化
double distance(Point& p) // 求距离
{
return sqrt((x-p.x)*(x-p.x)+(y-p.y)*(y-p.y)); // 欧几里得距离
}
};
// 定义节点
struct Node
{
Point point; // 栅格点
double g,h,f;// 代价值,f总价值,g到起点的代价值,h到终点的估计代价(启发式函数)
Node *parent;// 父节点指针
Node(Point point, double g, double h, Node* parent = nullptr):point(point), g(g), h(h), f(g+h), parent(parent)
{}
};

// 定义地图
vector<vector<int>> gridmap = {
{0, 1, 0, 0, 0},
{0, 0, 1, 0, 0},
{0, 0, 1, 1, 0},
{0, 0, 1, 0, 0},
{0, 0, 1, 1, 0}
};
// 定义起点和终点
Point start{0, 0};
Point goal{4, 4};
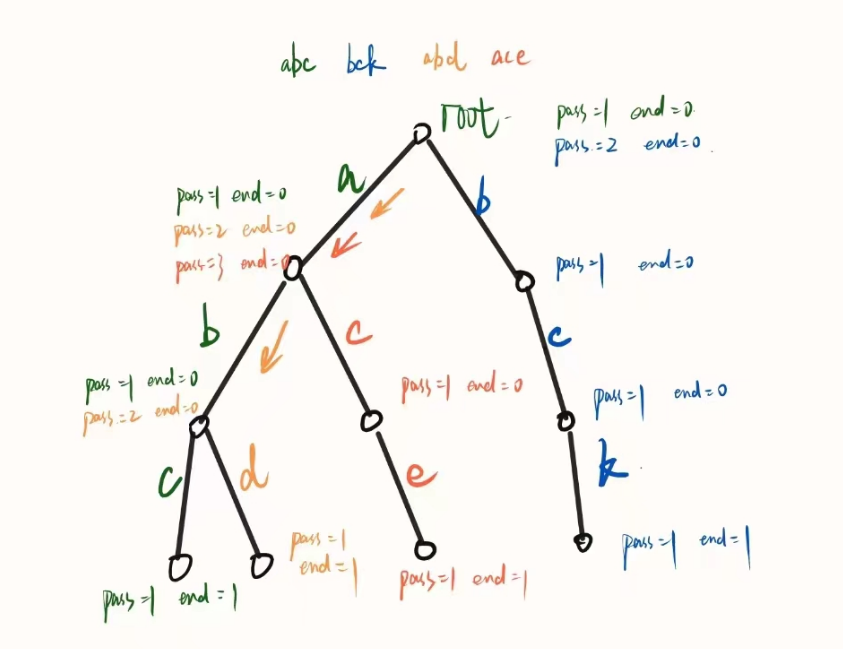
A*算法的寻路原理

A的结束条件

A算法的寻路详细步骤


手撕A*代码
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;
// 定义地图上的点
struct Point
{
int x,y; // 栅格行列
Point(int x, int y):x(x),y(y){}; // 参数列表初始化
double distance(Point& p) // 求距离
{
return sqrt((x-p.x)*(x-p.x)+(y-p.y)*(y-p.y)); // 欧几里得距离
}
};
// 定义节点
struct Node
{
Point point; // 栅格点
double g,h,f;// 代价值,f总价值,g到起点的代价值,h到终点的估计代价(启发式函数)
Node *parent;// 父节点指针
Node(Point point, double g, double h, Node* parent = nullptr):point(point), g(g), h(h), f(g+h), parent(parent)
{}
};
// 自定义Node*排序规则
struct NodeCompare{
bool operator()(Node* n1, Node* n2){
return (n1->f) < (n2->f); // 表示升序排列
}
};
// 基于栅格地图的路径规划A*算法,返回由Point组成的路径path,输入为地图,起点和终点
vector<Point> AstarPathPlanning(vector<vector<int>> &gridmap, Point& start, Point& goal)
{
// 获取地图参数
int row = gridmap.size(); // 行,表示地图的宽度
int col = gridmap[0].size(); // 列,表示地图的长
// 定义openlist, closelist
vector<Node *> openlist; // openlist 表示待搜索的节点
vector<Node *> closelist;// closelist表示已搜索的节点
openlist.push_back(new Node(start, start.distance(start), start.distance(goal))); // 将起点加入openlist中,作为初始化
int count1 = 1;
// 进入循环,开始搜索,搜索到终点则返回路径
vector<Point> path;
while (!openlist.empty()) // 当openlist为空,表示所有可搜索节点已经被搜索,此时循环结束
{
// 获取当前搜索节点current,即openlist中f最小节点
sort(openlist.begin(), openlist.end(), NodeCompare{}); // 先对openlist排序,这里自定义排序规则(从小到大)
Node* current = *openlist.begin(); // *openlist.begin()排序后即为f最小的迭代器位置
// 将current对应的元素从openlist中删除
openlist.erase(openlist.begin());
// 将current加入到closelist中
closelist.push_back(current);
// 对当前搜索节点current进行分类讨论
// 1-current是终点,则返回路径,表示找到路径
if (current->point.x == goal.x && current->point.y == goal.y)
{
while (current != nullptr) // 利用父节点,从终点向起点回溯最短路径,因为起点没有父节点,所以起点current父节点为nullptr
{
path.push_back(current->point);
current = current->parent;
}
reverse(path.begin(), path.end()); // 路径是反的,翻转路径
int count2 = 0; // delete 次数
for (auto o : openlist)
{
delete o;
count2++;
}
for (auto c : closelist)
{
delete c;
count2++;
}
cout << "new times: " << count1 << endl;
cout << "delete times: " << count2 << endl;
return path;
}
// 2-current 不是终点,需要讨论其邻近的节点neighbors
int x = current->point.x;
int y = current->point.y;
vector<Point> neighbors = { // 8个邻近节点的坐标
{x-1,y-1}, {x-1,y}, {x-1,y+1},
{x,y-1}, {x,y+1},
{x+1,y-1}, {x+1,y}, {x+1,y+1}
};
// 遍历所有的临近节点,每一个邻近节点n必须满足在地图范围内同时不是障碍物
for (auto n : neighbors)
{
if ((n.x >= 0 && n.x < row) && (n.y >= 0 && n.y < col) && gridmap[n.x][n.y]==0)
{
// 1 n在closelist中,表示已经搜索过了,此时直接跳过
bool incloselist = false;
for (auto c : closelist)
{
if (c->point.x == n.x && c->point.y == y)
{
incloselist = true;
break;
}
}
if (incloselist)
{
continue;
}
// 2 n是否在openlist中进行讨论
bool inopenlist = false;
for (auto o : openlist)
{
if (o->point.x == n.x && o->point.y == n.y)
{
inopenlist = true;
// n 在openlist中,对比f值,更新代价值和父节点parent
double g = current->g + n.distance(current->point); // 临近节点n到起点的距离 = 当前搜索节点current到起点的距离 + 当前搜索节点current到邻近节点n距离
double h = n.distance(goal); // 临近节点n到终点的估计距离代价
double f = g + h;
if (f < (o->f))
{
o->f = f;
o->parent = current;
}
break;
}
}
if (!inopenlist) // n不在openlist中,对比f值,计算代价值,添加到openlist中,下次备选
{
double g = current->g + n.distance(current->point); // 临近节点n到起点的距离 = 当前搜索节点current到起点的距离 + 当前搜索节点current到邻近节点n距离
double h = n.distance(goal); // 临近节点n到终点的估计距离代价
double f = g + h;
openlist.push_back(new Node(n,g,h,current));
count1++;
}
}
}
}
// 搜索完成没有路径,表示路径规划失败,此时返回空路径
return path;
}
int main()
{
// 定义地图
vector<vector<int>> gridmap = {
{0, 1, 0, 0, 0},
{0, 0, 1, 0, 0},
{0, 0, 1, 1, 0},
{0, 0, 1, 0, 0},
{0, 0, 1, 1, 0}
};
// 定义起点和终点
Point start{0, 0};
Point goal{4, 4};
vector<Point> path = AstarPathPlanning(gridmap, start, goal);
cout << path.size() << endl;
for (auto p : path)
{
if (p.x == goal.x && p.y == goal.y)
{
cout << "(" << p.x << ',' << p.y << ")" << endl;
}
else
{
cout << "(" << p.x << ',' << p.y << ")" << "->";
}
}
return 0;
}
A*算法总结
把起点加入 open list 。
重复如下过程:
a. 遍历 open list ,查找 F 值最小的节点,把它作为当前要处理的节点。
b. 把这个节点移到 close list 。
c. 对当前方格的 8 个相邻方格的每一个方格?
◆ 如果它是不可抵达的或者它在 close list 中,忽略它。否则,做如下操作。
◆ 如果它不在 open list 中,把它加入 open list ,并且把当前方格设置为它的父亲,记录该方格的 F , G 和 H 值。
◆ 如果它已经在 open list 中,检查这条路径 ( 即经由当前方格到达它那里 ) 是否更好,用 G 值作参考。更小的 G 值表示这是更好的路径。如果是这样,把它的父亲设置为当前方格,并重新计算它的 G 和 F 值。如果你的 open list 是按 F 值排序的话,改变后你可能需要重新排序。
d. 停止,当你
◆ 把终点加入到了 open list 中,此时路径已经找到了,或者
◆ 查找终点失败,并且 open list 是空的,此时没有路径。
3.保存路径。从终点开始,每个方格沿着父节点移动直至起点,这就是你的路径。