在线性回归中，函数求导是一个重要的数学工具，用于计算损失函数关于模型参数的导数。通过求导，我们可以找到最优的参数值，以实现更好的线性回归拟合。

本文将介绍线性回归的基本原理，以及如何通过函数求导来优化线性回归模型。

一、线性回归简介

线性回归是一种基本的机器学习方法，用于建立自变量和因变量之间的线性关系。通常情况下，我们假设自变量和因变量之间存在一个线性模型，即通过一条直线来拟合数据。

对于一维线性回归问题，我们可以表示为：y = mx + b，其中m是斜率，b是截距。对于多维线性回归问题，我们可以表示为：y = b0 + b1*x1 + b2*x2 + ... + bn*xn，其中b是截距，b1, b2, ..., bn是自变量的系数。

线性回归的目标是通过拟合的模型来预测新的自变量对应的因变量的值。为了使模型拟合良好，我们需要找到最优的参数值。

二、优化问题

在线性回归中，我们通过最小化损失函数来寻找最优的参数值。损失函数是衡量模型预测值与实际值之间差异的指标。

常用的损失函数是均方误差（Mean Squared Error，MSE），它是预测值与实际值之差的平方和除以数据点的数量。

对于一维线性回归问题，均方误差可以表示为：

MSE = (1/n) * Σ[yi - (mx + b)]^2

其中，n是数据点的数量，yi是实际值。

对于多维线性回归问题，均方误差可以表示为：

MSE = (1/n) * Σ[yi - (b0 + b1*x1 + b2*x2 + ... + bn*xn)]^2

我们的目标是找到最优的参数值，使得损失函数达到最小值。

三、函数求导

为了优化线性回归模型，我们需要计算损失函数关于模型参数的导数。导数是衡量函数变化率的指标，可以帮助我们找到函数的最小值或最大值。

在线性回归中，函数求导通过解析求导或数值求导两种方式实现。

1. 解析求导

解析求导是通过求取损失函数的导数公式进行计算。对于常见的函数，我们可以使用求导法则来计算导数。

对于一维线性回归问题，我们可以通过MSE公式对斜率m和截距b求导：

∂MSE/∂m = (-2/n) * Σ[yi - (mx + b)] * xi
∂MSE/∂b = (-2/n) * Σ[yi - (mx + b)]

对于多维线性回归问题，我们可以通过MSE公式对截距b和自变量系数bi求导：

∂MSE/∂b0 = (-2/n) * Σ[yi - (b0 + b1*x1 + b2*x2 + ... + bn*xn)]
∂MSE/∂bi = (-2/n) * Σ[yi - (b0 + b1*x1 + b2*x2 + ... + bn*xn)] * xi

解析求导方法能够精确计算导数，但对于复杂的函数和模型，求导可能比较复杂。

2. 数值求导

数值求导是通过有限差分计算导数。对于一个函数f(x)来说，它的导数可以近似计算为：

f'(x) = lim(h->0) [(f(x+h) - f(x)) / h]

对于线性回归中的函数求导，我们可以通过选取一个足够小的h值，计算两个函数值的差分来近似求导。

数值求导是一种直观简单的方法，适用于较为复杂的函数和模型。然而，它可能会引入一定的数值误差和计算复杂度。

四、梯度下降

通过函数求导，我们可以得到损失函数关于模型参数的梯度。梯度是多个偏导数构成的向量，表示函数在给定点的最大变化方向。

梯度下降是一种常用的优化算法，用于寻找函数的最小值。在线性回归中，我们可以使用梯度下降来更新模型参数，使得损失函数逐渐减小。

梯度下降的基本原理是通过不断减小损失函数的梯度来调整模型参数。具体步骤如下：

1. 初始化模型参数，包括斜率m和截距b。

2. 计算损失函数关于模型参数的梯度。

3. 根据学习率和梯度的方向和大小，更新模型参数。

4. 重复步骤2和步骤3，直到达到停止条件（如迭代次数达到指定值或损失函数变化较小）。

梯度下降算法能够帮助我们找到损失函数的最小值，从而实现更好的线性回归拟合。

五、总结

线性回归中的函数求导是优化模型的重要过程。通过求取损失函数关于模型参数的导数，我们可以获得关于模型拟合效果的有用信息，并通过优化算法来调整模型参数，实现更好的回归拟合。

通过理解和应用线性回归中的函数求导，我们可以更好地理解模型的优化过程，并且能够更准确地拟合和预测数据，实现有效的线性回归分析应用。

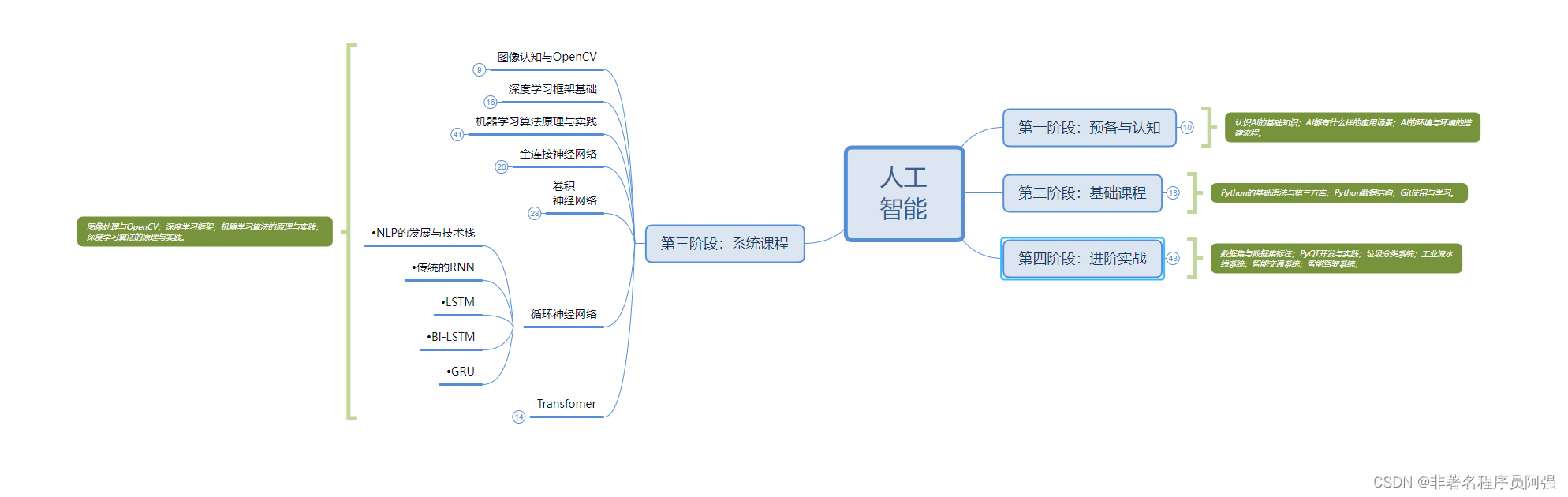
人工智能的学习之路非常漫长，不少人因为学习路线不对或者学习内容不够专业而举步难行。不过别担心，我为大家整理了一份600多G的学习资源，基本上涵盖了人工智能学习的所有内容。点击下方链接,0元进群领取学习资源,让你的学习之路更加顺畅!记得点赞、关注、收藏、转发哦!扫码进群领资料