第三十二章 数论——组合数的多种求法
- 一、数学基础
- 二、组合数——递推公式
- 1、题目
- 2、思路
- 3、代码
- 三、组合数——快速幂
- 1、问题:
- 2、分析
一、数学基础
组合数来自于高中排列组合的知识:
我们从 a a a个小球中随机一次性取出 b b b个,所有的取法记作: C a b C_a^b Cab
这个 C a b C_a^b Cab怎么算呢?
C a b = a ! b ! ( a − b ) ! C_a^b=\frac{a!}{b!(a-b)!} Cab=b!(a−b)!a!
二、组合数——递推公式
1、题目

2、思路
这道题如果我们强行用公式进行计算的话,我们一定是会超时的,为什么呢?
如果按照公式,我们需要算一个数的阶乘,那么数据范围是2000,这样的话,我们算阶乘所需的最大次数就是2000。
而我们是多组询问,这样的话,我们所需的时间就是100000*2000
这个次数就非常多了,因此基本上大概率超时了。
所以我们换一个方式:
我们在高中阶段曾经学过这样一个公式:
C
a
b
=
C
a
−
1
b
+
C
a
−
1
b
−
1
C_a^b=C_{a-1}^b+C_{a-1}^{b-1}
Cab=Ca−1b+Ca−1b−1
大家可以利用刚才的定义公式进行验证,当然这个也可以理解为我们后面的 01 01 01背包问题的状态转移方程。
这样做的好处是什么呢?
我们发现,我们这个递推公式是从小推大。
因此,我们在算出
c
[
a
]
[
b
]
c[a][b]
c[a][b]的时候,它前面的所有情况我们就都算出来了。
但是如果我们如果是采用刚刚的定义的话,我们每次查询都要计算一次。
而现在的话,我们可以通过一次计算预处理出来所有的情况。后续的查询只需要查表即可。这个时间复杂度就大大减少了。
3、代码
#include<iostream>
using namespace std;
const int N=2010;
const int mod=1e9+7;
int c[N][N];
void init()
{
for(int i=0;i<N;i++)
{
for(int j=0;j<=i;j++)
{
if(!j)c[i][j]=1;
else c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
}
}
int main()
{
int n;
init();
cin>>n;
while(n--)
{
int a,b;
scanf("%d%d",&a,&b);
printf("%d\n",c[a][b]);
}
return 0;
}
我们这里需要注意的是,我们的 c i 0 = 1 c_i^0=1 ci0=1。
很多同学会担心下标出现-1的情况,但其实经过我们的特判,它只会运行到:if(!j)c[0[0]=1;这一行,不会进行后续的代码。因此,不会出现越界的情况。
如果我们打印一下我们的预处理的话,我们发现这就是我们很熟悉的C语言练习题:杨辉三角

三、组合数——快速幂
1、问题:
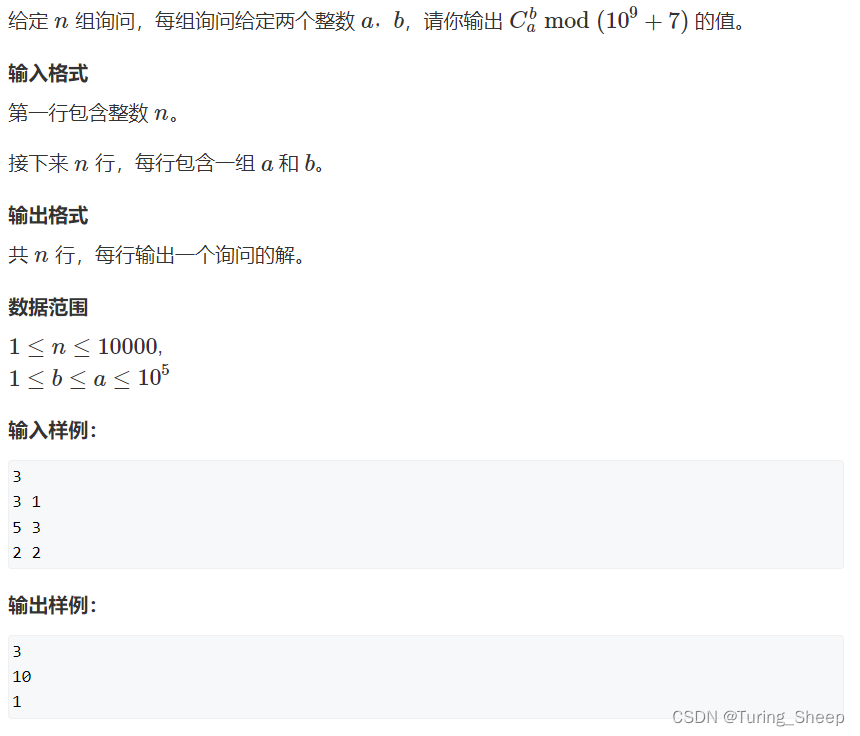
2、分析
这道题的关键在于我们 a a a和 b b b的范围是非常大的,所以我们很难通过开辟一个二维数组去预处理,不仅空间上很难找到这么大的一块空间,时间上也会出现很多多余的计算。
那么我们既然无法直接预处理最终的结果,我们可以根据定义预处理中间的过程。
根据我们的定义:
C a b = a ! b ! ( a − b ) ! C_a^b=\frac{a!}{b!(a-b)!} Cab=b!(a−b)!a!
我们可以去预处理出所有的阶乘,然后根据定义运算的时候直接查表。
但是这里有一个问题,就是说我们的最终结果是对 1 e 9 + 7 1e9+7 1e9+7取模的结果。
我们预处理的时候,为了避免溢出,我们存储的肯定是每个阶乘取模之后的结果。
所以我们计算的结果是这样的:
C a b = a ! % m b ! % m ( a − b ) ! % m C_a^b=\frac{a!\%m}{b!\%m(a-b)!\%m} Cab=b!%m(a−b)!%ma!%m
但是根据我们的模运算的法则:
a b % m ≠ a % m b % m \frac{a}{b}\%m\neq \frac{a\%m}{b\%m} ba%m=b%ma%m
因此,由于除法的出现,我们是无法正确计算出答案的。
那怎么办呢?
我们之前介绍过一个很重要的概念:乘法逆元
现在来回顾一下:
如果符合下面的同余式:
a b ≡ a ∗ x ( m o d c ) \frac{a}{b}\equiv a*x(mod\ c) ba≡a∗x(mod c)
那么我们就称 x x x是 b b b模 m m m的乘法逆元,记作: b − 1 b^{-1} b−1
这个式子其实并不好求逆元。
我们在之前的文章中还通过推导,发现上述的表达式还等价于:
b ∗ b − 1 ≡ 1 m o d ( c ) b*b^{-1}\equiv 1 mod(c) b∗b−1≡1mod(c)
如果
c
c
c是质数的话,我们可以使用费马小定理求解。
如果
c
c
c不是质数的话,我们可以使用扩展欧几里得算法求解。
这道题中我们的 1 e 9 + 7 1e9+7 1e9+7是质数,所以我们可以使用费马小定理。
我们先回顾一下费马小定理的式子:
b p − 1 ≡ 1 m o d ( p ) b^{p-1}\equiv 1mod(p) bp−1≡1mod(p)
即 b ∗ b p − 2 ≡ 1 m o d ( p ) b*b^{p-2}\equiv 1mod(p) b∗bp−2≡1mod(p)
因此我们的乘法逆元: b − 1 = b p − 2 b^{-1}=b^{p-2} b−1=bp−2
而这个结果我们可以使用快速幂求解。
我们现在思考一下,我们枚举的 i i i的逆元一定存在吗?
答案是一定的。
因为 1 e 9 + 7 1e9+7 1e9+7是质数,所以它和1到 1 e 9 + 6 1e9+6 1e9+6都是互质的。
即 g c d ( i , 1 e 9 + 7 ) = 1 gcd(i,1e9+7)=1 gcd(i,1e9+7)=1
根据裴蜀定理:
我们先令 m = 1 e 9 + 7 m=1e9+7 m=1e9+7
必有 x i + y m = 1 xi+ym=1 xi+ym=1
即 x i = − y m + 1 xi=-ym+1 xi=−ym+1
这个式子可以改写成:
x i ≡ 1 m o d ( m ) xi \equiv 1mod (m) xi≡1mod(m)
这个就是我们的逆元表达式, x x x就是我们要求的逆元,所以逆元必定存在。
这里还有一个问题:
我们的阶乘满足: n ! = n ∗ ( n − 1 ) ! n!=n*(n-1)! n!=n∗(n−1)!
那我们的逆元是否满足: n − 1 ! = n − 1 ∗ ( n − 1 ) − 1 ! n^{-1}!=n^{-1}*(n-1)^{-1}! n−1!=n−1∗(n−1)−1!呢?
答案是满足的。
n ∗ n − 1 ≡ 1 m o d ( m ) n*n^{-1}\equiv 1mod(m) n∗n−1≡1mod(m)
( n − 1 ) ∗ ( n − 1 ) − 1 ≡ 1 m o d ( m ) (n-1)*(n-1)^{-1}\equiv 1mod(m) (n−1)∗(n−1)−1≡1mod(m)
所以:
n
(
n
−
1
)
∗
(
n
−
1
)
−
1
n
−
1
≡
1
m
o
d
(
m
)
n(n-1)*(n-1)^{-1}n^{-1}\equiv 1mod(m)
n(n−1)∗(n−1)−1n−1≡1mod(m)
即: ( n − 1 ) − 1 n − 1 (n-1)^{-1}n^{-1} (n−1)−1n−1就是 n ( n − 1 ) n(n-1) n(n−1)的阶乘。所以由此不断地乘在一起,即可验证我们的结论。
那么代码怎么写呢?
#include<iostream>
using namespace std;
typedef long long LL;
const int N=1e5+10;
const int mod=1e9+7;
LL fact[N],infact[N];
LL qmi(LL a,LL b,LL p)
{
LL res=1;
while(b)
{
if(b&1)res=res*a%p;
a=a*a%p;
b>>=1;
}
return res%p;
}
void init()
{
fact[0]=1,infact[0]=1;
for(int i=1;i<N;i++)
{
fact[i]=i*fact[i-1]%mod;
infact[i]=infact[i-1]%mod*qmi(i,mod-2,mod)%mod;
}
}
int main()
{
init();
int n;
cin>>n;
while(n--)
{
int a,b;
scanf("%d%d",&a,&b);
LL ans=fact[a]%mod*infact[b]%mod*infact[a-b]%mod;
printf("%lld\n",ans);
}
return 0;
}