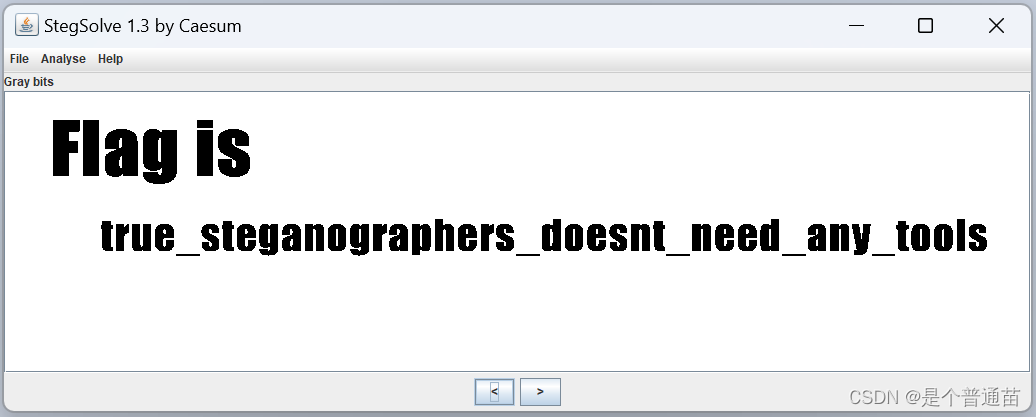
最优化理论
- 资料
- 一
- optimal condition 最优性条件
- 概念
- 二
- 一维搜索
- 逐次下降法iterative decent
- 单峰函数
- 二分法 dichotomous search
- 三
资料
B站最优化理论与算法
上交最优化方法
一
目标函数:需要优化的函数
决策变量,可以调整变化的量
约束集,决策变量的可行集
无约束优化,决策变量任意值
约束优化,决策变量范围有限制
非线性规划:代价函数或者约束是非线性的。
其他规划问题:
整数规划integer programming
混合整数规划 mixed integer programming
动态优化dynamic optimization
随机优化stochastic optimization
多目标优化multi objective optimization
博弈论 game theory
optimal condition 最优性条件
概念
-
凸集 convex set
-
hyperplane 超平面
超平面是n维欧氏空间中余维度等于一的线性子空间,也就是必须是(n-1)维度。
这是平面中的直线、空间中的平面之推广(n大于3才被称为“超”平面),是纯粹的数学概念,不是现实的物理概念。因为是子空间,所以超平面一定经过原点。 -
凸集边界点的支撑超平面
凸集所有点在该边界点支撑超平面的一侧,(凸集边界点的切线,或者过顶点的超平面) -
凸函数(小于等于)(严格凸(小于))
-
凹函数,-f(x) 凸函数,则f(x) 凹函数,定义域都是凸集
-
梯度,函数对多个自变量的偏导的矩阵
二阶梯度,hessian 阵,方阵,对称矩阵 -
单位向量,长度为一
-
方向导数,f(x) 的变化速率,梯度方向变化最快
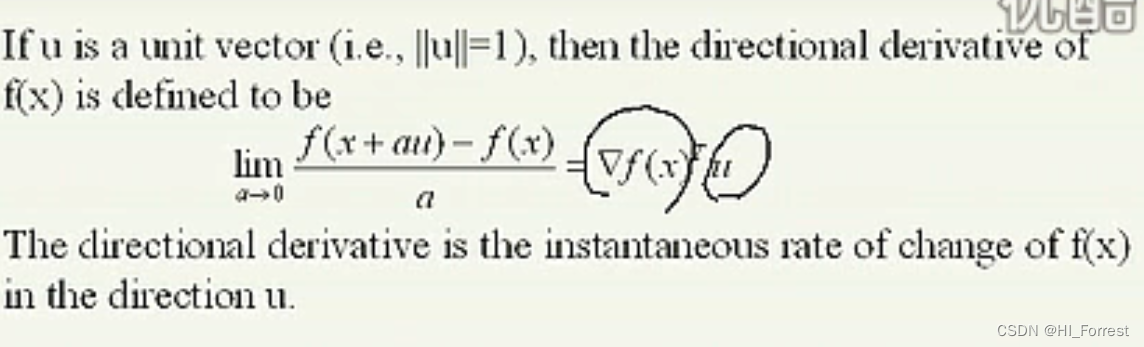
-
可导函数的凸性
1,
2, 开集,集合内的每个 x 的hessian阵 都是半正定矩阵, f(x) 是凸函数,充要条件。 -
矩阵正定:
1,对称阵H
2,任意非零向量x, x’ H x > 0
(负定小于0)
(半正定:x’ H x >=0)
对于n阶实对称矩阵A,下列条件是等价的:
(1)A是正定矩阵;
(2)A的一切顺序主子式均为正;
(3)A的一切主子式均为正;
(4)A的特征值均为正;
(5)存在实可逆矩阵C,使A=C′C;
(6)存在秩为n的m×n实矩阵B,使A=B′B;
(7)存在主对角线元素全为正的实三角矩阵R,使A=R′R [3] 。 -
泰勒展开

-
局部极小点
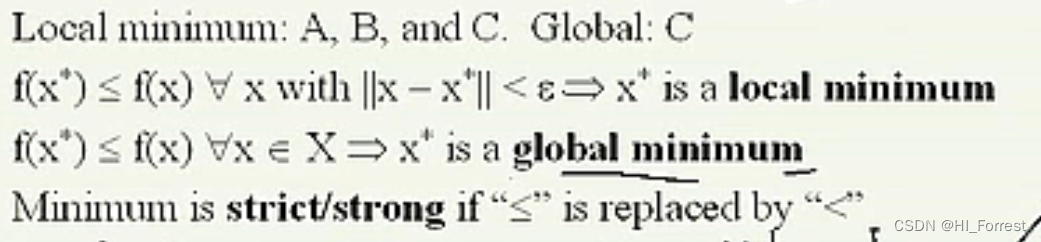
-
鞍点
沿一个方向是极小,另一个方向是极大

-
最优的充要条件

-
最优解的存在

有界闭集上定义的连续函数,有极值点(很多是在边界上)
二
一维搜索
逐次下降法iterative decent
从一个初始点x0出发,计算该点的局部信息
通过这些信息进行决策,选择一个合适的搜索方向
沿着该搜索方向找到下一个点x1,并围绕新的点计算局部信息
重复上述过程,找到一系列点xi(i = 1,2,…n),保证每次f(x)都能减小(如果目标是最小化函数)

单峰函数
单峰函数的定义
假设函数f(x)在区间[a,b]内的x*处有一个极小点:
那么说f(x)在区间[a,b]上是单峰的,即意味着对于区间[a,b]上的任意一个点x,当x趋向于x*的时候,f(x)的函数值都是减小的。
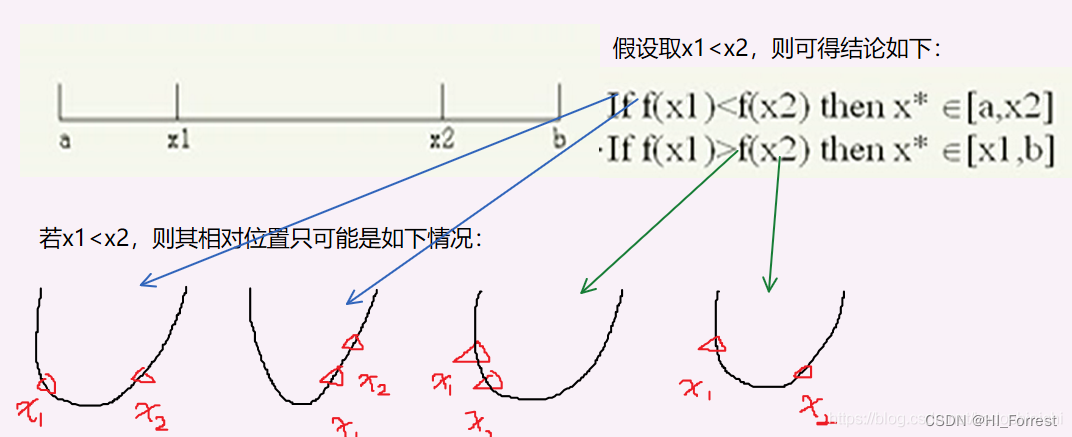
二分法 dichotomous search
根据上文提到的有关需要计算两个新的点,由此来决定新的区间的范围;
二分法就是通过区间中值来确定新区间的两个端点值。

两点等分搜索
三点等分搜索