基于C#实现Prim算法

news2024/9/28 11:24:00

图论在数据结构中是非常有趣而复杂的，作为 Web 码农的我，在实际开发中一直没有找到它的使用场景，不像树那样的频繁使用，不过还是准备仔细的把图论全部过一遍。

一、最小生成树

图中有一个好玩的东西叫做生成树，就是用边来把所有的顶点联通起来，前提条件是最后形成的联通图中不能存在回路，所以就形成这样一个推理：假设图中的顶点有 n 个，则生成树的边有 n-1 条，多一条会存在回路，少一路则不能把所有顶点联通起来，如果非要在图中加上权重，则生成树中权重最小的叫做最小生成树。
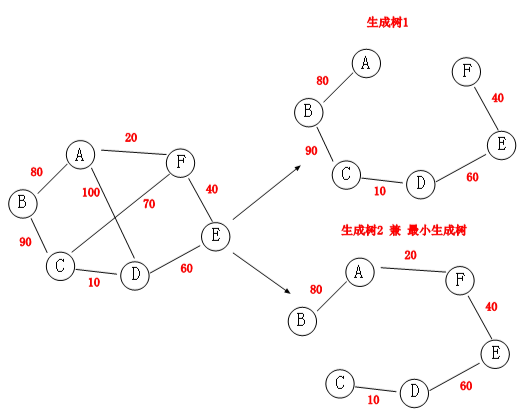
image.png
对于上面这个带权无向图来说，它的生成树有多个，同样最小生成树也有多个，因为我们比的是权重的大小。

二、Prim 算法

求最小生成树的算法有很多，常用的是 Prim 算法和 Kruskal 算法，为了保证单一职责，我把 Kruskal 算法放到下一篇，那么 Prim 算法的思想是什么呢？很简单，贪心思想。
如上图：现有集合 M={A,B,C,D,E,F}，再设集合 N={}。

  • 第一步：挑选任意节点（比如 A),将其加入到 N 集合，同时剔除 M 集合的 A。
  • 第二步：寻找 A 节点权值最小的邻节点（比如 F），然后将 F 加入到 N 集合，此时 N={A,F}，同时剔除 M 集合中的 F。
  • 第三步：寻找{A,F}中的权值最小的邻节点（比如 E），然后将 E 加入到 N 集合，此时 N={A,F,E}，同时剔除 M 集合的 E。
  • 。。。

最后 M 集合为{}时，生成树就构建完毕了，是不是非常的简单，这种贪心做法我想大家都能想得到，如果算法配合一个好的数据结构，就会如虎添翼。

三、代码

1、图的存储

图的存储有很多方式，邻接矩阵，邻接表，十字链表等等，当然都有自己的适合场景，下面用邻接矩阵来玩玩，邻接矩阵需要采用两个数组，
①. 保存顶点信息的一维数组，
②. 保存边信息的二维数组。

 public class Graph
 {
     /// <summary>
     /// 顶点个数
     /// </summary>
     public char[] vertexs;

     /// <summary>
     /// 边的条数
     /// </summary>
     public int[,] edges;

     /// <summary>
     /// 顶点个数
     /// </summary>
     public int vertexsNum;

     /// <summary>
     /// 边的个数
     /// </summary>
     public int edgesNum;
 }

2、矩阵构建

矩阵构建很简单，这里把上图中的顶点和权的信息保存在矩阵中。

 #region 矩阵的构建
 /// <summary>
 /// 矩阵的构建
 /// </summary>
 public void Build()
 {
     //顶点数
     graph.vertexsNum = 6;

     //边数
     graph.edgesNum = 8;

     graph.vertexs = new char[graph.vertexsNum];

     graph.edges = new int[graph.vertexsNum, graph.vertexsNum];

     //构建二维数组
     for (int i = 0; i < graph.vertexsNum; i++)
     {
         //顶点
         graph.vertexs[i] = (char)(i + 65);

         for (int j = 0; j < graph.vertexsNum; j++)
         {
             graph.edges[i, j] = int.MaxValue;
         }
     }

     graph.edges[0, 1] = graph.edges[1, 0] = 80;
     graph.edges[0, 3] = graph.edges[3, 0] = 100;
     graph.edges[0, 5] = graph.edges[5, 0] = 20;
     graph.edges[1, 2] = graph.edges[2, 1] = 90;
     graph.edges[2, 5] = graph.edges[5, 2] = 70;
     graph.edges[3, 2] = graph.edges[2, 3] = 100;
     graph.edges[4, 5] = graph.edges[5, 4] = 40;
     graph.edges[3, 4] = graph.edges[4, 3] = 60;
     graph.edges[2, 3] = graph.edges[3, 2] = 10;
 }
 #endregion

3、Prim

要玩 Prim，我们需要两个字典。
①：保存当前节点的字典，其中包含该节点的起始边和终边以及权值，用 weight=-1 来记录当前节点已经访问过，用 weight=int.MaxValue 表示两节点没有边。
②：输出节点的字典，存放的就是我们的 N 集合。
当然这个复杂度玩高了,为 O(N2)，寻找 N 集合的邻边最小权值时，我们可以玩玩 AVL 或者优先队列来降低复杂度。

 #region prim算法
 /// <summary>
 /// prim算法
 /// </summary>
 public Dictionary<char, Edge> Prim()
 {
     Dictionary<char, Edge> dic = new Dictionary<char, Edge>();

     //统计结果
     Dictionary<char, Edge> outputDic = new Dictionary<char, Edge>();

     //weight=MaxValue:标识没有边
     for (int i = 0; i < graph.vertexsNum; i++)
     {
         //起始边
         var startEdge = (char)(i + 65);

         dic.Add(startEdge, new Edge() { weight = int.MaxValue });
     }

     //取字符的开始位置
     var index = 65;

     //取当前要使用的字符
     var start = (char)(index);

     for (int i = 0; i < graph.vertexsNum; i++)
     {
         //标记开始边已使用过
         dic[start].weight = -1;

         for (int j = 1; j < graph.vertexsNum; j++)
         {
             //获取当前 c 的 邻边
             var end = (char)(j + index);

             //取当前字符的权重
             var weight = graph.edges[(int)(start) - index, j];

             if (weight < dic[end].weight)
             {
                 dic[end] = new Edge()
                 {
                     weight = weight,
                     startEdge = start,
                     endEdge = end
                 };
             }
         }

         var min = int.MaxValue;

         char minkey = ' ';

         foreach (var key in dic.Keys)
         {
             //取当前 最小的 key(使用过的除外)
             if (min > dic[key].weight && dic[key].weight != -1)
             {
                 min = dic[key].weight;
                 minkey = key;
             }
         }

         start = minkey;

         //边为顶点减去1
         if (outputDic.Count < graph.vertexsNum - 1 && !outputDic.ContainsKey(minkey))
         {
             outputDic.Add(minkey, new Edge()
             {
                 weight = dic[minkey].weight,
                 startEdge = dic[minkey].startEdge,
                 endEdge = dic[minkey].endEdge
             });
         }
     }
     return outputDic;
 }
 #endregion

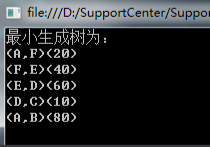
4、最后我们来测试一下，看看找出的最小生成树。

 public static void Main()
 {
     MatrixGraph martix = new MatrixGraph();

     martix.Build();

     var dic = martix.Prim();

     Console.WriteLine("最小生成树为：");

     foreach (var key in dic.Keys)
     {
         Console.WriteLine("({0},{1})({2})", dic[key].startEdge, dic[key].endEdge, dic[key].weight);
     }

     Console.Read();
 }

image.png

 using System;
 using System.Collections.Generic;
 using System.Linq;
 using System.Text;
 using System.Diagnostics;
 using System.Threading;
 using System.IO;
 using SupportCenter.Test.ServiceReference2;
 using System.Threading.Tasks;
 
 namespace ConsoleApplication2
 {
     public class Program
     {
         public static void Main()
         {
          MatrixGraph martix = new MatrixGraph();
 
             martix.Build();
 
             var dic = martix.Prim();
 
             Console.WriteLine("最小生成树为：");
 
             foreach (var key in dic.Keys)
             {
                 Console.WriteLine("({0},{1})({2})", dic[key].startEdge, dic[key].endEdge, dic[key].weight);
             }
 
             Console.Read();
         }
     }
 
     /// <summary>
     /// 定义矩阵节点
     /// </summary>
     public class MatrixGraph
     {
         Graph graph = new Graph();
 
         public class Graph
         {
             /// <summary>
             /// 顶点个数
             /// </summary>
             public char[] vertexs;
 
             /// <summary>
             /// 边的条数
             /// </summary>
             public int[,] edges;
 
             /// <summary>
             /// 顶点个数
             /// </summary>
             public int vertexsNum;
 
             /// <summary>
             /// 边的个数
             /// </summary>
             public int edgesNum;
         }
 
         #region 矩阵的构建
         /// <summary>
         /// 矩阵的构建
         /// </summary>
         public void Build()
         {
             //顶点数
             graph.vertexsNum = 6;
 
             //边数
             graph.edgesNum = 8;
 
             graph.vertexs = new char[graph.vertexsNum];
 
             graph.edges = new int[graph.vertexsNum, graph.vertexsNum];
 
             //构建二维数组
             for (int i = 0; i < graph.vertexsNum; i++)
             {
                 //顶点
                 graph.vertexs[i] = (char)(i + 65);
 
                 for (int j = 0; j < graph.vertexsNum; j++)
                 {
                     graph.edges[i, j] = int.MaxValue;
                 }
             }
 
             graph.edges[0, 1] = graph.edges[1, 0] = 80;
             graph.edges[0, 3] = graph.edges[3, 0] = 100;
             graph.edges[0, 5] = graph.edges[5, 0] = 20;
             graph.edges[1, 2] = graph.edges[2, 1] = 90;
             graph.edges[2, 5] = graph.edges[5, 2] = 70;
             graph.edges[3, 2] = graph.edges[2, 3] = 100;
             graph.edges[4, 5] = graph.edges[5, 4] = 40;
             graph.edges[3, 4] = graph.edges[4, 3] = 60;
             graph.edges[2, 3] = graph.edges[3, 2] = 10;
         }
         #endregion
 
         #region 边的信息
         /// <summary>
         /// 边的信息
         /// </summary>
         public class Edge
         {
             //开始边
             public char startEdge;
 
             //结束边
             public char endEdge;
 
             //权重
             public int weight;
         }
         #endregion
 
         #region prim算法
         /// <summary>
         /// prim算法
         /// </summary>
         public Dictionary<char, Edge> Prim()
         {
             Dictionary<char, Edge> dic = new Dictionary<char, Edge>();
 
             //统计结果
             Dictionary<char, Edge> outputDic = new Dictionary<char, Edge>();
 
             //weight=MaxValue:标识没有边
             for (int i = 0; i < graph.vertexsNum; i++)
             {
                 //起始边
                 var startEdge = (char)(i + 65);
 
                 dic.Add(startEdge, new Edge() { weight = int.MaxValue });
             }
 
             //取字符的开始位置
             var index = 65;
 
             //取当前要使用的字符
             var start = (char)(index);
 
             for (int i = 0; i < graph.vertexsNum; i++)
             {
                 //标记开始边已使用过
                 dic[start].weight = -1;
 
                 for (int j = 1; j < graph.vertexsNum; j++)
                 {
                     //获取当前 c 的 邻边
                     var end = (char)(j + index);
 
                     //取当前字符的权重
                     var weight = graph.edges[(int)(start) - index, j];
 
                     if (weight < dic[end].weight)
                     {
                         dic[end] = new Edge()
                         {
                             weight = weight,
                             startEdge = start,
                             endEdge = end
                         };
                     }
                 }
 
                 var min = int.MaxValue;
 
                 char minkey = ' ';
 
                 foreach (var key in dic.Keys)
                 {
                     //取当前 最小的 key(使用过的除外)
                     if (min > dic[key].weight && dic[key].weight != -1)
                     {
                         min = dic[key].weight;
                         minkey = key;
                     }
                 }
 
                 start = minkey;
 
                 //边为顶点减去1
                 if (outputDic.Count < graph.vertexsNum - 1 && !outputDic.ContainsKey(minkey))
                 {
                     outputDic.Add(minkey, new Edge()
                     {
                         weight = dic[minkey].weight,
                         startEdge = dic[minkey].startEdge,
                         endEdge = dic[minkey].endEdge
                     });
                 }
             }
             return outputDic;
         }
         #endregion
     }
 }

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1242893.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

电脑出现api-ms-win-crt-runtime-l1-1-0.dll丢失的情况有什么解决办法，dll文件丢失的方法

电脑出现api-ms-win-crt-runtime-l1-1-0.dll丢失的情况有什么解决办法，dll文件丢失的方法

在使用电脑过程中&#xff0c;有时可能会遇到缺失api-ms-win-crt-runtime-l1-1-0.dll文件的问题&#xff0c;这可能导致某些应用程序无法正常运行。本文将介绍三种解决这个问题的方法&#xff0c;并比较它们的优缺点。 一.解决api-ms-win-crt-runtime-l1-1-0.dll丢失的问题 方…
阅读更多...
再添千万级罚单，某银行年内罚款过亿！金融行业合规问题亟待解决

再添千万级罚单，某银行年内罚款过亿！金融行业合规问题亟待解决

11月17日晚间&#xff0c;国家金融监管总局上海监管局披露行政处罚信息显示&#xff0c;某银行因32项违法违规事实收到两张690万元的大额罚单&#xff0c;合计罚款金额达1380万元。但这并不是银行该今年收到的第一张大额罚单。今年4月28日&#xff0c;该行因在结售汇、外币理财…
阅读更多...
C语言——接受一个整形值（无符号），使用函数的递归，按照顺序打印他的每一位。

C语言——接受一个整形值（无符号），使用函数的递归，按照顺序打印他的每一位。

#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>void print(int n) {if(n>9){print(n/10);}printf("%d ",n%10); }int main() {unsigned int num 0;scanf("%d", &num);print(num);return 0; }
阅读更多...
【Redis】前言--redis产生的背景以及过程

【Redis】前言--redis产生的背景以及过程

一.介绍 为什么会出现Redis这个中间件&#xff0c;从原始的磁盘存储到Redis中间又发生了哪些事&#xff0c;下面进入正题 二.发展史 2.1 磁盘存储 最早的时候都是以磁盘进行数据存储&#xff0c;每个磁盘都有一个磁道。每个磁道有很多扇区&#xff0c;一个扇区接近512Byte。…
阅读更多...
Colmap三维重建详解与使用方法

Colmap三维重建详解与使用方法

图片捕获过程&#xff0c;请遵循以下指导方针以获得最佳重建结果: 1 捕捉具有良好纹理的图像。避免使用完全没有质感的图片(例如&#xff0c;白色的墙或空桌子)。如果场景本身没有足够的纹理&#xff0c;你可以放置额外的背景对象&#xff0c;如海报等。 2 在相似的照明条件下…
阅读更多...
Linux常用命令指南以及shell脚本编程

Linux常用命令指南以及shell脚本编程

常用快捷键 Tab键补齐命令CtrlA键光标移动到最前CtrlE键光标移动到最后CtrlU键清空当前输入的内容上/下键切换之前输入的命令 文件操作 cd test进入test目录cd…返回上一个目录cd.停留在当前目录 .代表当前目录ls显示当前文件夹下面的所有文件/文件夹等ls -all显示当前文件夹…
阅读更多...
柯桥生活日语学习，打工人的日语你会吗？

柯桥生活日语学习，打工人的日语你会吗？

打工人在日语里有几种说法: アルバイト 这是最常用的称呼,直接对应中文的“打工”。 例句: 学生の頃はスーパーでアルバイトをしていた。(我学生时代在超市打过工。) バイト これはアルバイトの略称でよく使われる。(这是アルバイト的简称,也很常用。) 例句: バイト先が決…
阅读更多...
gitea仓库镜像同步至gitlab

gitea仓库镜像同步至gitlab

1、参考文档&#xff1a;仓库镜像 | Gitea Documentation 2、错误一&#xff1a;账号密码错误问题 解决方法&#xff1a; 出现以上错误为第三步用户名&#xff08;Oauth2应用名称&#xff09;或者密码&#xff08;Gitlab个人访问令牌&#xff09;错误。 1&#xff09;如下图1…
阅读更多...
【攻防世界-misc】pure_color

【攻防世界-misc】pure_color

1.方法一&#xff1a;用画图工具打开图片&#xff0c;将图片拷贝至虚拟机win7桌面&#xff0c; 点“属性”&#xff0c;颜色设置为“黑白”&#xff0c; 出现flag值。 2.方法二&#xff1a;使用Stegsilve打开&#xff0c;分析图片 将图片打开&#xff0c;按左右键查找&#xff…
阅读更多...
Linux常用基础命令及重要目录，配置文件功能介绍

Linux常用基础命令及重要目录，配置文件功能介绍

目录 一&#xff0c;Linux常用必备基础命令 1&#xff0c;网络类命令 2&#xff0c;文件目录类命令 3&#xff0c;操作类命令 4&#xff0c;关机重启命令 5&#xff0c;帮助命令 6&#xff0c;查看显示类命令 7&#xff0c;命令常用快捷键 二&#xff0c;Linux重要目录…
阅读更多...
【Linux】：消息队列和信号量

【Linux】：消息队列和信号量

信号 一.消息队列1.原理2.消息队列的各种接口1.创建消息队列2.释放消息队列3.发送和接收信息 二.信号1.概念2.各种接口1.创建信号量2.销毁信号量3.对信号量进行操作 三.一个现象 一.消息队列 1.原理 这种消息队列被称为system V标准。 可以使用ipcs -q来查询消息队列&#xff…
阅读更多...
Jmeter+influxdb+grafana监控平台在windows环境的搭建

Jmeter+influxdb+grafana监控平台在windows环境的搭建

原理&#xff1a;Jmeter采集的数据存储在infuxdb数据库中&#xff0c;grafana将数据库中的数据在界面上进行展示 一、grafana下载安装 Download Grafana | Grafana Labs 直接选择zip包下载&#xff0c;下载后解压即可&#xff0c;我之前下载过比较老的版本&#xff0c;这里就…
阅读更多...
【git】pip install git+https://github.com/xxx/xxx替换成本地下载编译安装解决网络超时问题

【git】pip install git+https://github.com/xxx/xxx替换成本地下载编译安装解决网络超时问题

目录 &#x1f311;&#x1f311; 背景 &#x1f312; &#x1f312;作用 &#x1f314;&#x1f314; 问题 &#x1f314;&#x1f314;解决方案 &#x1f319;方法一 &#x1f319;方法二 &#x1f31d;&#x1f31d;我的解决方案 整理不易&#xff0c;欢迎一键三连…
阅读更多...
Exception in thread “消费者“ java.lang.IllegalMonitorStateException

Exception in thread “消费者“ java.lang.IllegalMonitorStateException

这两天学习生产者消费者模型的时候&#xff0c;使用Java线程来实现&#xff0c;出现了一个问题“Exception in thread "消费者" java.lang.IllegalMonitorStateException”&#xff0c;并且&#xff0c;线程不结束。报错图片如下&#xff1a; 那我们怎么解决呢&…
阅读更多...
品牌小红书koc投放策略分享，纯干货！

品牌小红书koc投放策略分享，纯干货！

作为中国具有影响力的时尚美妆社交平台&#xff0c;小红书与其充满活力的用户群体成为品牌寻找优质KOC合作的理想平台。本文伯乐网络传媒将探讨品牌如何利用小红书的KOC投放策略&#xff0c;实现更广泛的市场覆盖和更有效的品牌营销。 一、明确目标受众与KOC合作需求 在开始策…
阅读更多...
创新建筑形式：气膜体育馆助力校园体育设施革新

创新建筑形式：气膜体育馆助力校园体育设施革新

体育场馆在校园中扮演着重要的角色&#xff0c;是学生们进行体育锻炼、比赛和各类体育活动的场所。传统的室内体育馆建设往往需要大量资金和漫长的建设周期&#xff0c;但随着气膜体育馆的崭露头角&#xff0c;校园体育设施的面貌正迎来一场革新。 快速搭建&#xff0c;灵活性极…
阅读更多...
2023亚太杯数学建模APMCM竞赛C题思路讲解：基于ARIMA与机理模型进行预测

2023亚太杯数学建模APMCM竞赛C题思路讲解：基于ARIMA与机理模型进行预测

本文针对6大问题,从多角度分析了我国新能源电动汽车发展形势与前景。文中针对不同问题,采用了层次分析法、时间序列模型、机理模型、回归模型等数学方法。并结合实例数据,对相关模型进行求解,以量化预测了新能源电动汽车在政策驱动、市场竞争、温室气体减排等多个方面的潜在贡献…
阅读更多...
这样写Allure生成测试报告，学会直接涨薪5k

这样写Allure生成测试报告，学会直接涨薪5k

Allure是一个开源的测试报告生成框架&#xff0c;提供了测试报告定制化功能&#xff0c;相较于我们之前使用过pytest-html插件生成的html格式的测试报告&#xff0c;通过Allure生成的报告更加规范、清晰、美观。 pytest框架支持使用Allure生成测试报告&#xff0c;接下来让介绍…
阅读更多...
低代码开发与IT开发的区别

低代码开发与IT开发的区别

目录 一、含义不同 二、开发门槛不同 三、两者之间的区别 1、从技术特征来看 2、从目标开发者来看 四、低代码平台使用感受&#xff1f; &#xff08;1&#xff09;自定义模块&#xff0c;满足不同的业务需求 &#xff08;2&#xff09;工作流引擎&#xff0c;简化复杂流程的管…
阅读更多...
什么是数据确权？

什么是数据确权？

在数字化时代&#xff0c;数据已经成为一种新型资产&#xff0c;”新的石油“&#xff0c;具有巨大的价值&#xff0c;未来世界经济竞争一定程度上是数字经济的竞争&#xff0c;而非工业的竞争。数据相关法律制度&#xff0c;尚且还不完整&#xff0c;推动数字经济的发展&#…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023