说明：

1. 文章内容为对KMP算法的总结，以及力扣例题；
2. 文章内容为个人的学习总结，如有错误，欢迎指正。

1. KMP算法

1.1 算法步骤

KMP算法通常用于字符串的匹配，解题分两步：

1. 构建模式串的next数组。
   一般来说next数组就是前缀表（不太准确，但差不多是那个意思）。next[i]表明当第i个元素不匹配时应该回退到哪个位置：
   比如第i个元素不匹配，此时应寻找i之前的子串的最长相同前后缀的长度，这个长度的值就是next[i-1]的值。
   例：aab当i指向‘b’是发生了失配，此时应寻找b之前的子串，即‘aa’的最长相同前后缀的长度（=1），也就是说此时i指针应回退到下标为1的位置继续比较
2. 匹配
   即模式串与主串的匹配。两个指针i，j分别指向主串和模式串，若二者匹配则两个指针后移；若发生失配，则指向模式串的指针j进行回退，重新匹配。

1.2 关于指针回退问题

关于指针回退的问题，我梳理一下：
例如：

主串='aabaabaaf'
模式串='aabaaf'

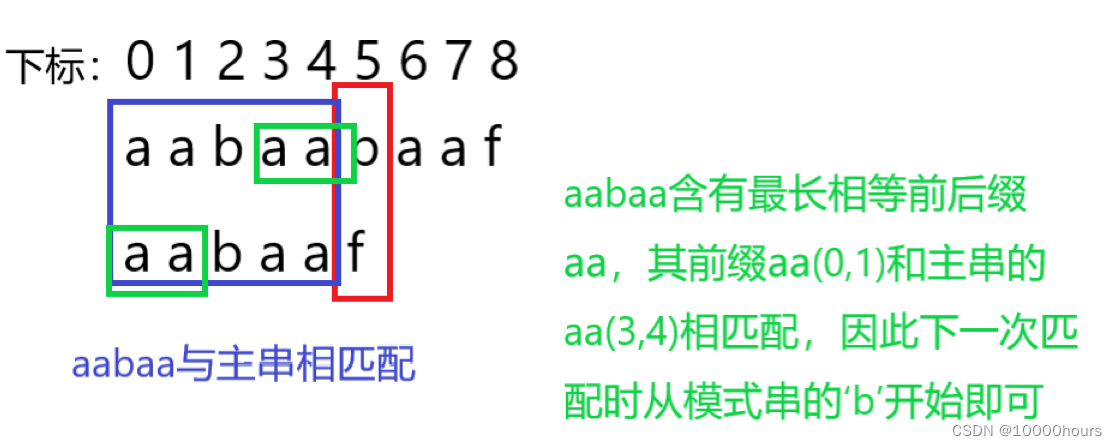
1. 匹配时，模式串的‘f’与主串的‘b’不匹配，此时模式串的指针应该回退，但是回退到哪个位置呢？KMP算法告诉我们应该回退到模式串‘b’的位置，为什么呢？

2. 因为不匹配的‘f’之前的子串——‘aabaa’的最长相同前后缀长度为2，即‘b’的下标。‘f’失配，但是‘aabaa’是和主串相匹配的，也就是说模式串中的“aa”（下标为3,4）与主串中的“aa”（下标为3,4）是相匹配的，而且子串“aabaa”中，后缀“aa”有最长相同的前缀“aa”（下标为0,1），也就是说这个前缀“aa”（下标0,1）和主串中的“aa”（下标为3,4）也是相匹配的，所以无需重复比较，直接将指针回退到模式串的‘b’位置继续比较即可。
   

3. 所以next[i]中存储的是i以及i以前的子串的最长相同前后缀长度。那么当i发生失配时，就要找i以前（0~i-1）的子串的最长相同前后缀长度是多少，然后回退到这个位置。
   比如‘f’失配时，要找‘f’之前的子串的最长相同前后缀长度（aabaa的最长相同前后缀长度）

2 . LeetCode例题

28. 找出字符串中第一个匹配项的下标

class Solution {
public:
    int strStr(string haystack, string needle) {
        vector<int> next(needle.size(),0);
        getNext(next, needle); //创建needle的next数组
        
        int j=0;
        for(int i=0; i<haystack.size(); i++){
            while(j>0 && haystack[i]!=needle[j])
                j = next[j-1];//发生失配，j进行回退
            if(haystack[i] == needle[j])
                j++;
            if(j == needle.size())
                return (i - needle.size() +1);//主串中出现了模式串，返回第一次出现模式串的下标
        }
        return -1; //主串中没有出现模式串，返回-1
    }

    void getNext(vector<int>& next, string needle){
        int n = needle.size();
        int j = 0; //j指向前缀的末尾
        next[0] = 0;//初始化nums[0]
        for(int i=1; i<n; i++){//j从0开始，则i从1开始，i指向后缀的末尾，初始前后缀的长度都是1
            while(j>0 && needle[i]!=needle[j])
                j = next[j-1];//前后缀的末尾不匹配，j指针进行回退
                            //j指针的回退相当于减小前缀的长度，当前缀末尾和后缀末尾相同时，此时就找到了needle[i]（包括needle[i]）之前的最长相同前后缀的长度；否则最长相同前后缀长度为0
            if(needle[i] == needle[j]){
                j++; //前后缀末尾相同时，同时后移i，j指针
            }
            next[i] = j;//将j的位置赋值给next[i]，表明第i个元素发生失配时应该回退到哪个位置
        }
    }
};