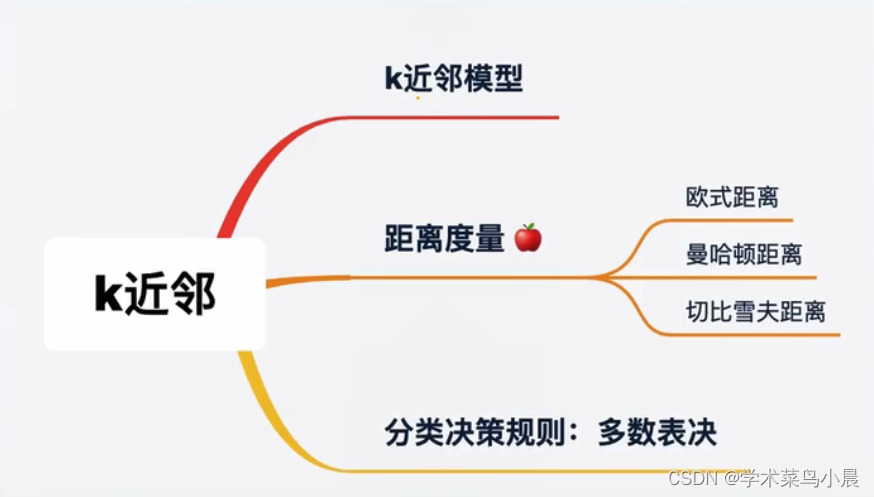
K-nearest neighbor
知识树
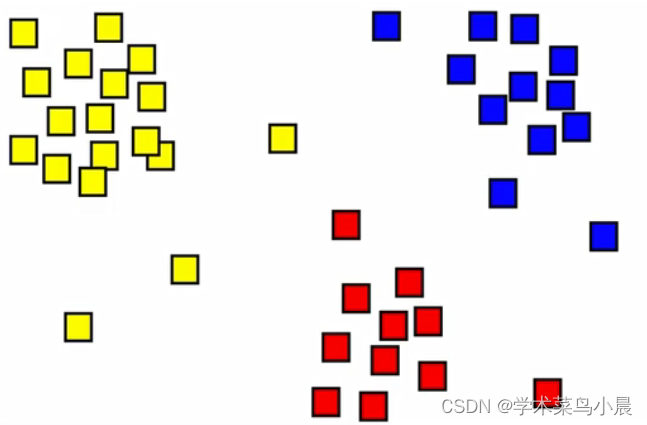
怎么区分红豆绿豆?
How to distinguish red beans and green beans?

之前我们构造了一个超平面来解决这个问题,既然超平面可以切分,是不是红豆之间和绿豆之间有着某种关联。即:物以类聚。
如果一个豆过来自然而然的到红豆堆,我们有理由认为它大概率是红豆。
-
同一标签的样本通常有很多相似的特征。
-
没进来一个样本,查看它周边的样本是什么类别,那么它就很有可能属于该类别。
那么某个点与其它点距离怎么计算。
距离度量
Distance measure
首先令

度量的方法有:
欧式距离(也称二范数):

xi里的x减去对应位置的xj里的x,然后全部平方,再求和,然后开根号。
如果两个点之间的距离很远,那么值就会很大
曼哈顿距离(也称一范数/也称城市街区距离):

相对上面欧式距离,不需要平方-相加-开根号,只要拿它的绝对值-相加即可
P范数:

引出P范数,p=1则是一范数,p=2则是二范数
还有3范数(也称切比雪夫距离/棋盘距离)
最常用的是欧式距离>曼哈顿距离>切比雪夫距离
总结
Summarization
-
K近邻思想:物以类聚
-
K近邻没有显式的训练过程
-
不需要先训练再预测,直接得到结果
-
-
距离度量
-
欧式距离:两点之间直线
-
曼哈顿距离:城市街区距离
-
切比雪夫距离:棋盘距离
-
K值的选择
How to chose K
选择较小的K值
用较小的邻域进行预测。预测结果对邻近的实例点非常敏感。如果邻近的实例点恰好是噪声,预测就会出错。
选择较大的K值:
用较大的邻域进行预测。对于输入实例较远(已经不太相似)的样本点也会对预测起作用,使预测发生错误。
在应用中:
先取一个较小的K值,再通过交叉验证法来选取最优的K值
分数表决规则
Majority voting rule
分类决策规则:多数表决
损失函数:


实心圆内都判断为红色的损失值


实心圆内都判断为蓝色的损失值

K近邻算法
K-nearest neighbor
输入:训练数据T = [(x1, y1),...,(xn,yn)]

实例特征向量x。
-
根据给定的距离度量,在训练集中找到与x最近的k个点,涵盖这k个点的邻域记作Nk(x)
-
在Nk(x)中根据分类决策规则(如多少表决)决定x的类别y
输出实例x所属的类别y
总结
Summarization
-
K近邻的思想:物以类聚
-
K近邻没有显式的训练过场
-
距离度量:欧式距离、曼哈顿距离、切比雪夫距离
-
分类方式:多数表决规则