信息系统的三大定律(摩尔定律,梅特卡夫定律,吉尔德定律)有一个清晰的视角:
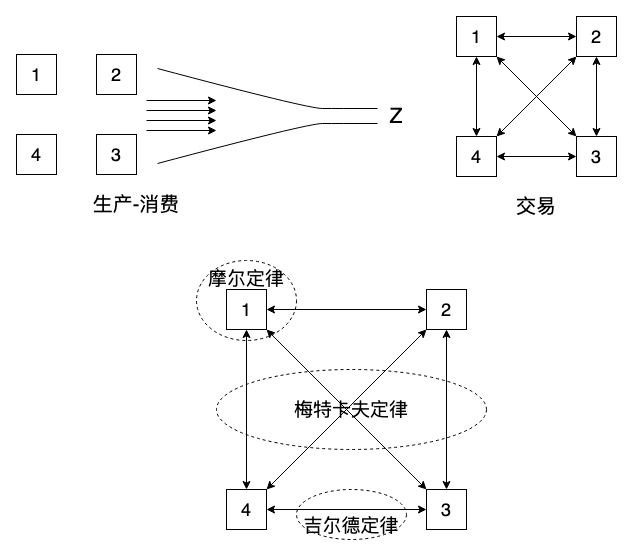
信息系统不是左边的生产消费系统,而是右边的交易系统,交易系统与生产消费典型的区别在于信息交易过程会产生新的信息,就像钱一样。
梅特卡夫定律说的网络价值随网络节点数指数增长。看似神秘的定律很容易用数学表述,一个网络有 n 个节点,新增 1 个节点,就新增 kn 潜在流量,再新增 1 个节点,就新增 k(n+1) 潜在流量,m 个节点就有 km(m-1) 潜在流量。如果在一个真实的通信网络,以上规律将对终端和转发节点提出同样的要求,即系统能力必须指数增长。
这很明显是摩尔定律的另一种说法,这就是摩尔定律指数的成因,因为芯片要么是信息的来源,计算,要么是信息的归宿,存储,无论计算还是存储,只有指数增长才能应对不断接入的信息需求。
就算终端没有联网,独立终端也是一个网络,指数增长的根源在于芯片内部以及主板都是交易系统,输入和输出像雪崩一样指数积累。这是一个需求驱动的网络,每一种新的应用需求就像接入了一个节点一样。
至于 18~24 个月,则受制于技术创新和工艺,以及一些商业约束。
因此摩尔定律和梅特卡夫定律就是一回事。
吉尔德定律稍有不同,它利用的是光波的物理特征,而人们(显然不是经理)开发这种物理特征的能力则是指数级增长的,大概和摩尔定律同步。如果世界上没有互联网,甚至没有一张联通的网络,人们开发无限带宽的欲望将大大降低。
摩尔,梅特卡夫,吉尔德这之间的关系非常有趣,梅特卡夫根据自己的定律预言互联网一定会拥塞崩溃,对互联网持悲观态度,而吉尔德则表示互联网不会崩溃,因为根据自己的定律,再大流量也有无限带宽兜着,摩尔则在一旁笑而不语,你们讨论的一切流量还不是始发于芯片,然而芯片的能力也不是无限雪崩的,他坦言自己的摩尔定律将失效,哈哈。
于是,世界重新变得静寂?
其实这种事在其它领域早已有之,只是那些领域不是互联网信息交易的主场,大多数争论都隐藏在大学研究院或高端论坛的高墙之后。马尔萨斯预言人口指数级增长将造成资源崩溃,但进入 20 世纪后,人们称马尔萨斯理论过时了。
同样,2008 年开始,有人预测房价会无限以大于 1 的指数增长下去,而收入只是线性增长,如果不赶紧买,会越来越买不起。类似的,有多少人预测某 700,某 baba 的市值会无限增长,工资 all in 了股票,结果呢…
凡指数增长的东西,一开始都不被在意,等发现时就是恐惧,最终恐惧的事情并没有发生,一切重归静寂,好像一个大玩笑。一切这种定律的背后总有个极限抓手,在将要崩溃的边缘悬崖勒马,人们适应这种约束。
IPv4 地址在互联网初期也是指数级需求增长,专家们呼吁部署一个明显过度设计的 IPv6,但 IPv4 并没有在短时间内耗尽。
倾向于组合现有技术,用多样性解决问题,空间换时间或反过来,而不是颠覆性变革技术基底。哥斯拉巨兽不会存在,因为它的体重会压垮自身,历史并没有为满足哥斯拉而进化出硅基身体托住它巨大的体重,满足不了就不费劲了,进化为了适应,不适的就抛弃,特征的进化存在极限。
任何定律都是某个范围内近似,为了预测而不是为了描述。任何结论都是多种因素共同促成的,没有任何单一定律能描述所有因果。
很多人认为吉尔德定律是骗人的,2000 年前后的互联网泡沫,整个 2010 年代的光纤通信大爆发,都要归罪和归功于这个吉尔德的预言,过了 2010 年,人们发现这个预言不对,无限带宽并没有达到,网络依然拥塞,于是断言吉尔德骗了人。
事实上吉尔德定律是有效的,只是无限带宽并非端到端带宽,而是骨干,比如 DWDM,在骨干网,几乎已经宣布了 “笨网” 相对于 “大软件” 智能网的大胜。我们知道,端到端问题源自用户的惰性,网络边缘一直是众口难调,恰恰适时出现的移动互联网又打破了梅特卡夫的预设,就显得混乱了。
梅特卡夫认为,由于骨干 “一定会崩溃”,局域网才会是主角,摩尔定律加持下,他们认为未来的 PC 一定会越来越智能,但恰恰出现了手机,把网线给拔了,现如今终端网络几乎没有有线局域网,几乎都是 LTE/5G or WiFi,而这两类技术各有各的包袱,以至于它们均无法适应吉尔德的无限带宽。
LTE/5G 来自电信阵营,而 WiFi 则是一个 CSMA 网络。吉尔德在他的经典著作《通信革命》里喷了电信阵营的胖网瘦端技术,比如 ATM,而对于 CSMA 网络,它本身就是一个 “无限抖动” 的网络,谁见谁愁,总有人试图用魔改 bbr 适应 WiFi,简直就是用精确的预设适应一个随机的现实。
总之很有意思,摩尔定律将要失效,梅特卡夫的网络将崩溃,都悲观,只有吉尔德乐观憧憬无限带宽,结果还出现了偏差…
下面是书摘:

作者写这本书时,ATM 技术,Microsoft Windows 如日中天。
浙江温州皮鞋湿,下雨进水不会胖。