序列检测
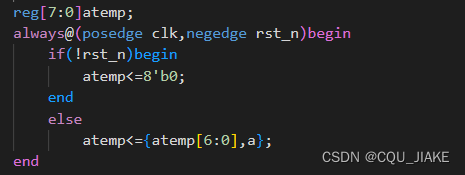
用一个atemp存储之前的所有状态,即之前出现的七位
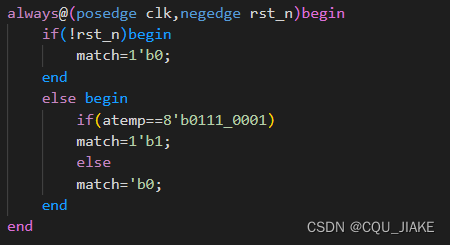
含无关项检测
要检测011XXX110
对于暂时变量的高位,位数越高就是越早出现的数字,因为新的数字存储在TEMP的最低位
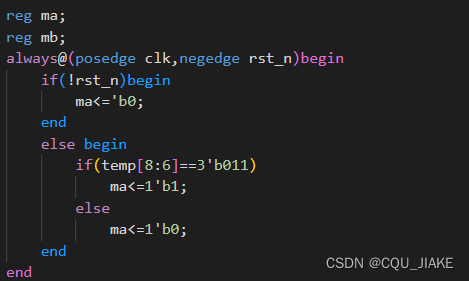
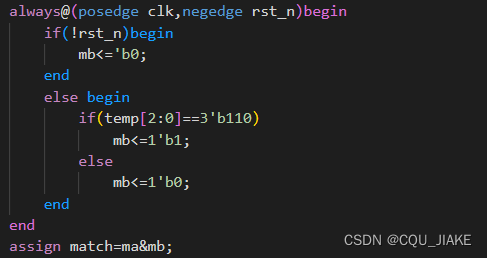
不重叠序列检测
,一组一组
011100
`timescale 1ns/1ns
module sequence_detect(
input clk,
input rst_n,
input data,
output reg match,
output reg not_match
);
parameter ZERO=0, ONE=1, TWO=2, THREE=3, FOUR=4, FIVE=5, SIX=6, FAIL=7;
reg [2:0] state, nstate;
reg [2:0] cnt;
always@(posedge clk or negedge rst_n) begin
if(~rst_n)
cnt <= 0;
else
cnt <= cnt==6? 1: cnt+1;
end
always@(posedge clk or negedge rst_n) begin
if(~rst_n)
state <= ZERO;
else
state <= nstate;
end
always@(*) begin
if(~rst_n)
nstate = ZERO;
else
case(state)
ZERO : nstate = data? FAIL : ONE;
ONE : nstate = data? TWO : FAIL;
TWO : nstate = data? THREE: FAIL;
THREE: nstate = data? FOUR : FAIL;
FOUR : nstate = data? FAIL : FIVE;
FIVE : nstate = data? FAIL : SIX;
SIX : nstate = data? FAIL : ONE;
FAIL : nstate = cnt==6? ZERO: FAIL;
default: nstate = ZERO;
endcase
end
always@(*) begin
if(~rst_n) begin
match = 0;
not_match = 0;
end
else begin
match = cnt==6&&state==SIX;
not_match = cnt==6&&state==FAIL;
end
end
endmodule


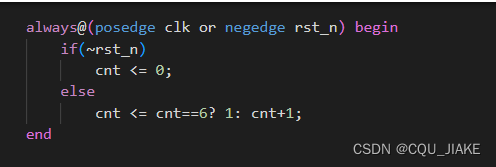
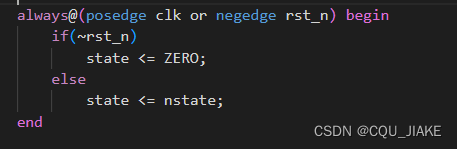
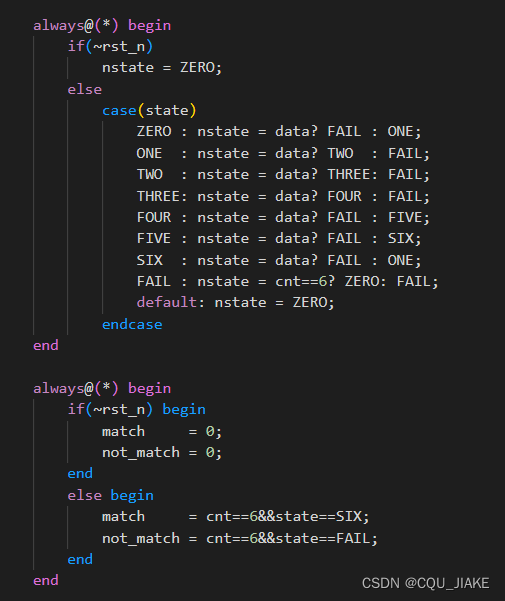
状态机代码
状态机简写为FSM
非阻塞赋值可以理解为次态,就是当前时间步结束后,在下一个时间步将右侧表达式的值应用到被赋值的信号上,从而实现状态的更新
module StateMachine(
input wire clk,
input wire reset,
output wire [1:0] state
);
reg [1:0] current_state, next_state;
always @(posedge clk or posedge reset) begin
if (reset)
current_state <= 2'b00;
else
current_state <= next_state;
end
always @(current_state) begin
case(current_state)
2'b00: next_state <= 2'b01; // State transition from 00 to 01
2'b01: next_state <= 2'b10; // State transition from 01 to 10
2'b10: next_state <= 2'b00; // State transition from 10 to 00
default: next_state <= 2'b00;
endcase
end
assign state = current_state;
endmodule两种状态机
Mealy状态机的输出信号取决于现态与输入;
Moore状态机仅取决于当前状态,即现态
Moore
module moore(
input wire clk,
input wire a,
output wire b,
output wire[1:0]state
);
reg[1:0]current_state;
wire b_out;
parameter s0=2'b00;
parameter s1=2'b01;
parameter s2=2'b10;xzz
always@(posedge clk)begin
case(current_state)
s0:begin
if(a)begin
current_state<=s1;
b_out<=1'b0;
end
end
s1:begin
if(!a)begin
current_state<=s2;
b_out<=1'b1;
end
end
s2:begin
if(a)begin
cs<=s0;
b<=1'b1;
end
end
endcase
end
assign b=b_out;
assign state=cs;
end在摩尔状态机中,每个状态都有一个特定的输出值,该输出值在进入该状态时被分配并保持不变,直到状态发生转移
reg [:] current_state ;
reg [:] next_state ;
wire [:0] IDLE ;
wire [:0] S0 ;
wire [:0] S1 ;
wire [:0] S2 ;
//=============================================================================\
//**************************** State Machine *******************************
//=============================================================================\
always @(posedge sclk or negedge s_rst_n) begin
if(!s_rst_n)
current_state <= IDLE;
else
current_state <= next_state;
end
always @(*) begin
next_state = IDLE;
case(current_state)
IDLE:begin
if(idle2s0 == 1'b1)
next_state = S0;
else
next_state = current_state;
end
S0:begin
if(s02s1 == 1'b1)
next_state = S1;
else
next_state =current_state;
end
S1:begin
if(s12s2 == 1'b1)
next_state = S2;
else
next_state = current_state;
end
S2:begin
if(s22idle == 1'b1)
next_state = IDLE;
else
next_state = current_state;
end
default:begin
next_state = IDLE;
end
endcase
end
assign idle2s0 = current_state == IDLE &&
assign s02s1 = current_state == S0 &&
assign s12s2 = current_state == S1 &&
assign s22idle = current_state == S2 &&
always @(posedge sclk or negedge s_rst_n) begin
if(!s_rst_n) begin
end
else begin
case(next_state)
end
endalways(*)会在输入信号变化时自动执行
在每个状态内部,检查特定的输入信号条件,如果满足,就将次态设置为特定值,不然,就将次态保留为现态
在状态转移的逻辑中使用阻塞,因为阻塞赋值会按照代码的顺序逐行执行,并立即更新被赋值的变量,在状态转移逻辑中,使用阻塞赋值可以确保在同一个时间步内只有一个状态转移会被执行
非阻塞赋值允许在同一个时间步内同时更新多个变量的值,将右侧表达式的值保存在一个暂存器内,然后在时间步的末尾将暂存器的值赋给左侧,可以确保所有变量在同一个时间步内同时更新,保持状态的一致性。在状态转移逻辑中使用阻塞赋值可以按顺序进行状态检查和状态转移,而在时钟驱动的逻辑中使用非阻塞赋值可以模拟时序行为,确保状态的同步更新。
在摩尔状态机中,在每个时钟上升沿,状态机会根据当前状态和输入信号计算出下一个状态,并在下一个上升沿时更新输出,因此需要等待时钟的到来才能进行状态转移和生成输出
摩尔状态机的当前输出总是在一个周期后,米利状态机中,输入更改会在逻辑完成后立即导致输出更改
摩尔状态机
以一个序列检测器为例,检测到输入信号11时输出z为1,其他时候为0。用摩尔型FSM实现需要用到三个状态(A,B,C)。而用米利型FSM实现则需要两个状态(A,B)。摩尔型FSM输出函数的输入只由状态变量决定,要想输出z=1,必须C状态形成,即寄存器中的两个1都打进去后才可以。输出z=1会在下一个有效沿到来的时候被赋值。而米利型FSM输出函数是由输入和状态变量共同决定的。状态在B的时候如果输入为1,则直接以组合电路输出z=1,不需要等到下个有效沿到来。从而也就不需要第三个状态C。
是输出函数仅取决于当前状态,而不是状态转移仅取决于当前状态
就是说,米利与摩尔状态机的状态转换,肯定都取决于现态与输入,只不过米利状态机的输出是要取决于输入与现态,然后摩尔的输出直取决于现态。
也就是说,有多少种输出信号,摩尔状态机就需要额外增加多少种状态,在这个状态下,才会输出相应的信号
而对于米利状态机,只需要提供输出这个信号时的现态即可,从这个现态延申出输出信号
就比如说两道题,每道ABCD选项;
用摩尔状态机的话,就需要1(初始状态)+2*2种状态
2*2就是选对与没选对的状态,即第一道题选对了,第二道题对了的状态,输出一个分数
第一道题选对了,第二道题错了的状态,输出一个分数
第一道题选错了,第二道题对了的状态,输出一个分数
第一道题选错了,第二道题错了的状态,输出一个分数
摩尔状态机就是一个树形的结构,需要有节点记录决策后的结果
而米利状态机,只需要记录决策的节点即可
即米利状态机需要1+2种状态,即两道题决策的状态,输出函数,就取决在在这个决策状态(现态)与决策(输入信号)
那么在上例种,可以认为第一位与第二位就是要决策的状态,所以米利状态机至少需要两个状态,而摩尔状态机至少要三个,需要有额外的节点状态来负责输出。即想要输出1,必须要进入状态C
检测11,只有第一位是1时,摩尔与米利状态机进入A状态;在此基础上,只有第二位是1时,进入B状态;此时,米利状态机就不需要新状态了,摩尔状态机还需要一个新状态,来记录最终的输出
就是说,米利状态机的每个状态,是每个状态节点还未进行决策时的情况;而摩尔状态机是已经做出决策的状况。就是第一位,A状态,对米里而言,是要做第一位的决策,还不知道做的结果是什么,取决于输入。而摩尔的第一位,B状态,是已经做出了决策,且决策是1,那么就进入B状态
初始状态,摩尔是A,米利是A,摩尔的A是真初始状态,表示还没有任何结果,初始化的一个状态;米利可以理解为要做第一个决策,但还不知道结果是什么的一个状态,也可以认为是初始状态
那么对摩尔状态转移就是,只有为1时,才会进入下一个状态,C就是都为1的状态。在状态转移过程种不输出,在状态节点上进行输出,可以认为摩尔状态机的状态,是记录结果的状态。
对米利状态转移就是,做出不同的选择会进入不同的状态,只有为1才会进入下一个状态(下一次决策前的状态),其输出,在转移的过程中进行输出,也就是给到输入后,就意味着此时的决策已经知道,就进入下个状态,是记录决策节点的状态,其输出在由最后的节点延申出的线条当中
摩尔与米利检测1101
所以按照上面的思路,摩尔与米利状态机检测1101,分别需要5和4种状态
摩尔的话,就是纯初始状态,以及4个匹配成功的状态,只要不断的匹配成功才会进入下个状态;记录的是结果;即S0代表初始,S1,S2,S3,S4分别代表每位都匹配成功的结果;S1记录第一位正确,第二位待定。S2记录第一位第二位正确,第三位待定……
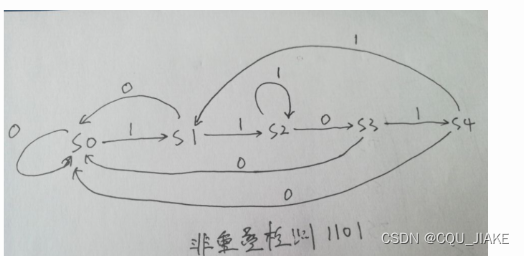
代码

米利与摩尔状态机都要有这样的代码块,即并不是这个原因导致摩尔
米利的话,就是4个位要确定的状态,也是只有确定匹配才会进入下个状态。记录的是要进行选择时的状态;即S0,S1,S2,S3分别代表每位未确定前的状态,即IDLE,S0就是第一位待定……第一位确定,第二位待定……
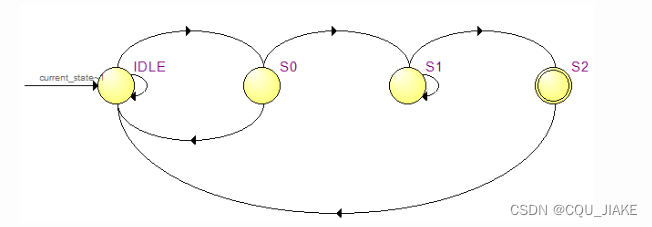
所以按照上面的思路,摩尔状态机要慢一个周期,因为确定结果,进行非阻塞赋值要在当下这个周期结束后才进行;而米利状态机,知道当下状态,知道输入信号,就可以在当下周期用ASSIGN输出信号

按键消抖
软件按键消抖模块:软件算法通常通过软件延时和状态机来实现按键消抖。当检测到按键状态变化时,软件会进行一定的延时,以等待按键抖动稳定。在延时结束后,再次检测按键状态,只有当连续多次检测到相同的按键状态时,才确认按键的有效触发。
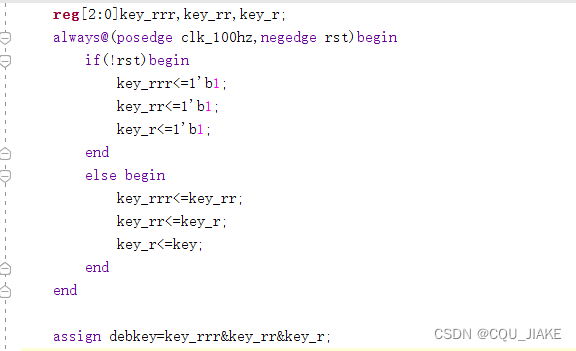
就是说,在连续的三个时间周期内,检测到的按键值都一样,那就可以认为按键已经稳定下来了,也就可以进行采用了
![]()
这个就是用来检测三个按键是否相同,寄存器分别寄存上一个状态