👨‍🎓个人主页：研学社的博客 

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

旅行推销员问题（TSP）是运筹学、数学优化和理论计算领域的经典算法问题。推销员必须绕过最短路线并返回起点，访问一定数量的地方。精确算法和启发式算法都用于求解 TSP.
旨在获得具有因子复杂性的精确解的精确算法被归类为 NP-Complete。启发式方法的解决方案要么基于优化问题。这些算法的复杂性小于确切的算法。因此，它在更少的时间和空间内给出解决方案，并在近似解决方案足以解决问题的情况下使用，特别是在达到确切解决方案非常困难的情况下。
本文的第一个目的是强调每种TSP方法的要求，局限性和功能，以指导科学家和研究人员选择最适合其特定需求的方法。它对最有效和广泛使用的TSP方法进行了全面调查，通过研究旨在发现其优势和劣势的方法来澄清其主要差异。
蚁群优化 （ACO） 考虑一种启发式方法，该方法具有达到最佳 TSP 解决方案的强大能力。它来源于蚂蚁在自然界中的自然行为——基于分析真正的蚂蚁思考在蚁群中寻找和储存食物。本论文的第二个目的是提出一种新的混合算法来解决TSP。它将由ACO与邻居加入（NJ）组合而成的结构，并称之为（NACO）。新算法高度关注所有可能影响解决方案的标准并将其应用于 TSP，并且通过将它们与蚁群的原始算法进行比较，特别是在减少计算和时间方面，它对解决方案进行了许多改进。
此外，本文还介绍了并行NACO作为高性能TSP的高效并行程序。建议在单独的执行线程中并行运行 Ant，以受益于每个 ant 的独立操作，并使用多核系统实现并行算法。提出的程序由MATLAB® R2017a（版本9.2）编程，并在具有8GB RAM和Intel Core i7-8565U CPU，64位Windows操作系统的HP计算机上实施。结果表明，相对于NACO，复杂度降低到O（n^2（n-ω））。至PNACO，复杂性从O（n（n⁄p）（n-ω））降低，此外加速度高达10。

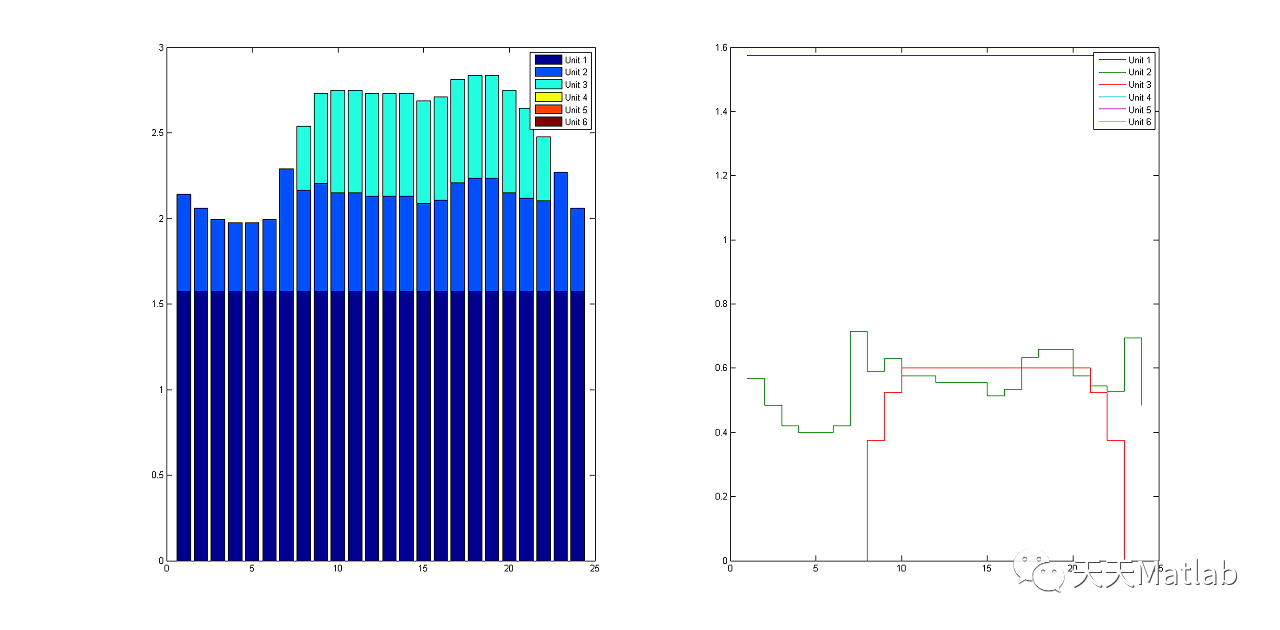
📚2 运行结果

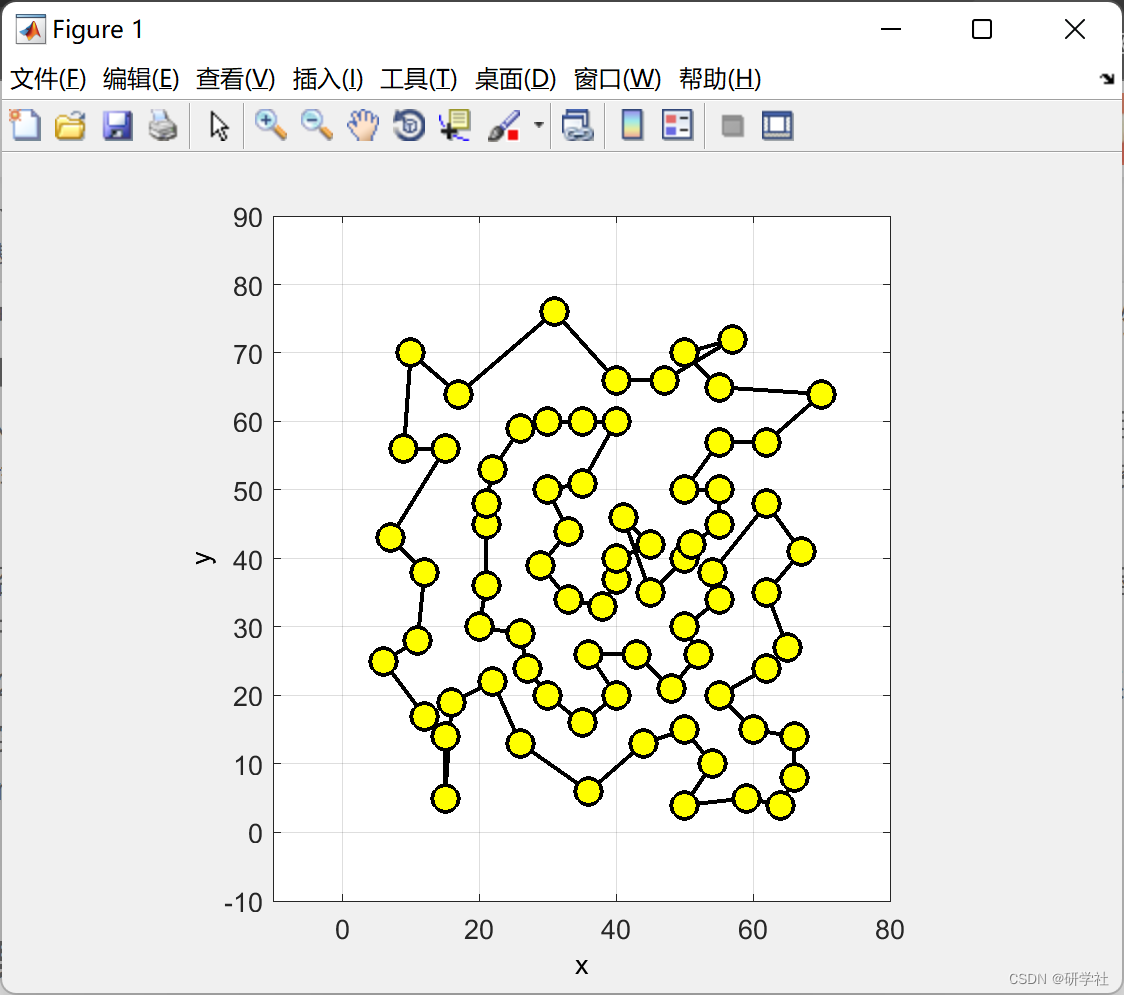
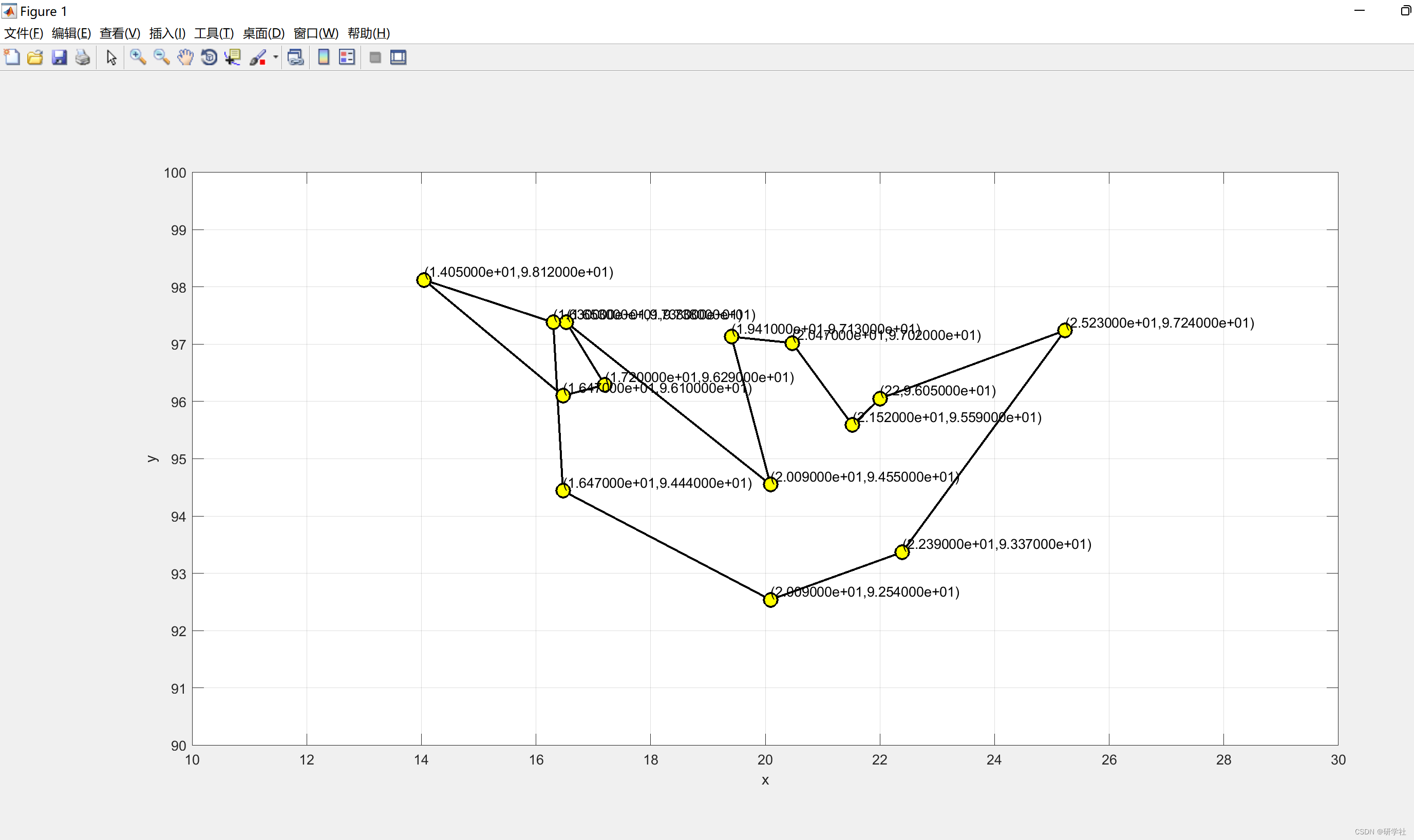
部分代码：

%% The Parameters

Iteration=1;                          % No. of Iterations
no_ant=1;                             % Population Size (No. of Ants)
Q=100;
%t0=1;
t0=10*Q/(no_Var*mean(D_Set.D(:)));      % Initial Phromone
alpha=1;                                % Phromone Exponential Weight
beta=5;                                 % Heuristic Exponential Weight
rate=0.7;                              % Evaporation Rate

%% Initialization

eta=1./D_Set.D;                         % Heuristic Information Matrix
t=t0*ones(no_Var,no_Var);               % Phromone Matrix
BC=zeros(Iteration,1);                  % Array to Hold Best Cost Values

% Empty Ant
empty_ant.Tour=[];
empty_ant.Cost=[];

% Ant Colony Matrix
ant=repmat(empty_ant,no_ant,1);

% Best Ant
BS.Cost=inf;

% the Level_one of NJ
Leaf=Leaf_1(D_Set.D);

% Runtime
T_1 = cputime;

%% NEW_ACO Main Program

for it=1:Iteration    
    for k=1:no_ant                      % Move Ants
        Leaf1=Leaf;
        ant(k).Tour=randi([1 no_Var]);  %% {choose a random non visited city}
        city=ant(k).Tour;
        for l =2:no_Var
            ant_tour=ant(k).Tour(end);          
            [row,col] = find(Leaf1==city);
            
            if isempty(row)
                P=t(ant_tour,:).^alpha.*eta(ant_tour,:).^beta;           
                P(ant(k).Tour)=0;
                P=P/sum(P);
                city=RouletteSelection(P);
                ant(k).Tour=[ant(k).Tour city];
            else
                l=l+1;                  % Pass the joining cities 
                if col==2
                    city=Leaf1(row,1);
               else
                    city=Leaf1(row,2);
                end
                ant(k).Tour=[ant(k).Tour city];
                Leaf1(row,1)=0;
                Leaf1(row,2)=0;
            end
          %  ant(k).Tour=[ant(k).Tour city];
        end
        ant(k).Cost=CostFunction(ant(k).Tour);
        
        if ant(k).Cost<BS.Cost
            BS=ant(k);
        end
    end
     
    % Update Phromones
    for k=1:no_ant
        tour=ant(k).Tour;
        tour=[tour tour(1)]; 
        for ll=1:no_Var
            ant_tour=tour(ll);
            city=tour(ll+1);
            t(ant_tour,city)=t(ant_tour,city)+Q/ant(k).Cost;
        end
        
    end
    
    % Evaporation
    t=(1-rate)*t;
    
    % Store Best Cost
    BC(it)=BS.Cost;

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]A HYBRID OPTIMIZATION ALGORITHM OF ANT COLONY SEARCH AND NEIGHBOUR-JOINING METHOD TO SOLVE THE TRAVELLING SALESMAN PROBLEM"‏, Advanced Mathematical Models & Applications Vol.5, No.1, 2020, pp.95-110

🌈4 Matlab代码实现