文章目录
- 深度优先搜索遍历算法的实现
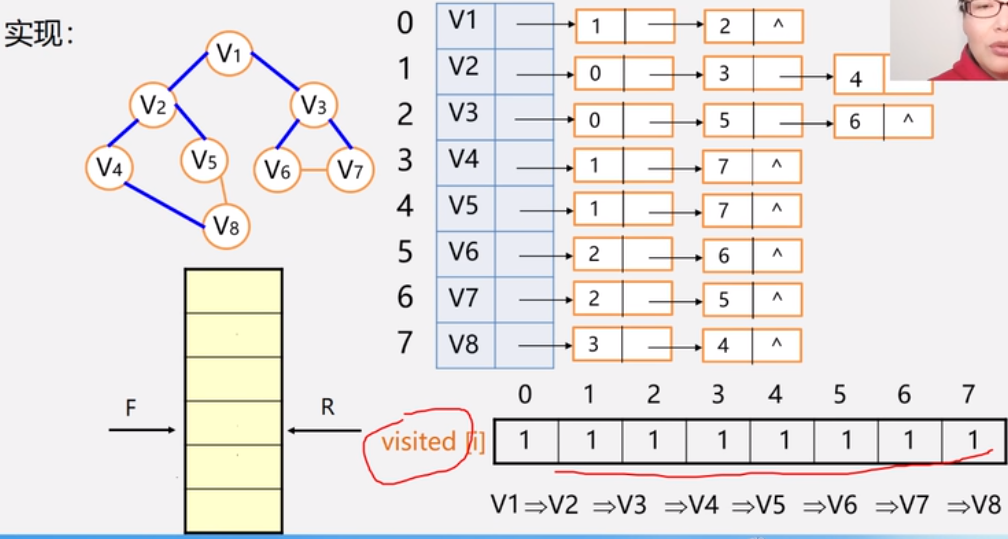
- 邻接矩阵表示的无向图深度遍历实现:
- DFS算法分析
- 广度优先遍历(BFS-Breadth_First Search)
- 构造最小生成树
深度优先搜索遍历算法的实现
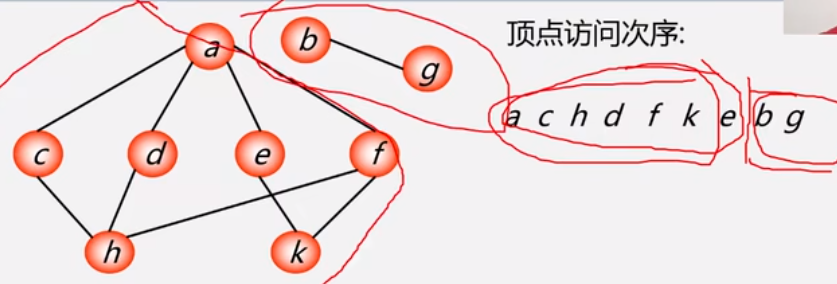
邻接矩阵表示的无向图深度遍历实现:
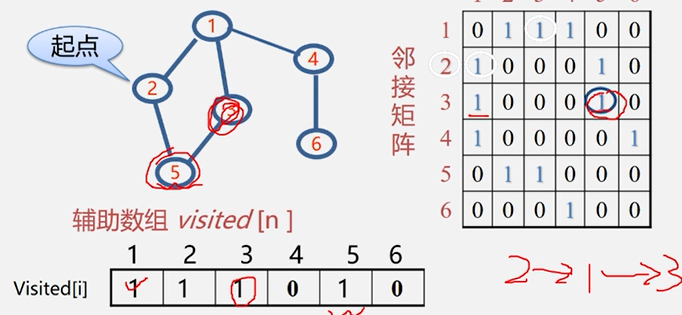
实现深度优先遍历的关键在于回溯。就是自后往前,追溯曾将走过的路径。
算法的特点:
- 深度优先算法是一个递归的过程。
- 首先,选定一个出发点后再进行遍历,如果有邻接的未被访问过的结点则继续前进。
- 若不能继续前进,则回退一步再前进。
- 若回退一步仍不能继续前进,则连续回退至可以前进的位置为止。
- 重复此过程,直到所有与选定点相通的所有顶点都被遍历。
- 若重复此过程,直到所有与选定点相通的顶点都被遍历。
- 深度优先搜索是递归过程,带有回退操作,因此需要使用栈存储访问的路径信息。当访问到的当前顶点没有可以前进的邻接结点的时候,需要进行出栈操作,将当前位置回退到栈元素的位置。
DFS算法分析
用邻接矩阵来表示图,遍历图中每一个顶点都要从头扫描该顶点所在行,时间复杂度为O(n的平方)。
用邻接表来表示图,虽然有2e个表结点,但只需e个结点即可完成遍历,加上访问
个头结点的时间,时间复杂度为O(n+e)。
结论:
稠密图适于在邻接矩阵上进行深度遍历;
稀疏图适于在邻接表上进行深度遍历。
非连通图的遍历
广度优先遍历(BFS-Breadth_First Search)
方法:从图的某一结点出发,首先依次访问该结点的所有邻接结点Vi1,Vi2,…,Vin再按这些顶点被访问的先后次序依次访问与他们相邻接的所有未被访问过的顶点。
重复此过程,直至所有顶点均被访问完为止。
例: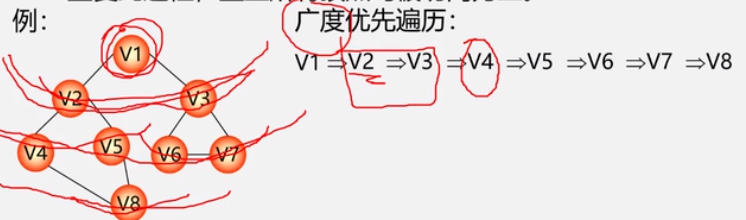
利用队列来实现
概念回顾----生成树
生成树:所有顶点均由边连接在一起,但不存在回路的图。
- 一个图可以有许多棵不同的生成树
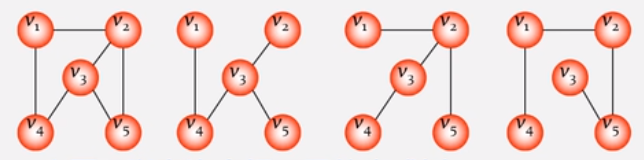 - 所有生成树具有以下共同特点:
- 所有生成树具有以下共同特点:
- 生成树的顶点个数与图的顶点个数相同;
- 生成树是图的极小连通子图,去掉一条边则非联通;
- 一个有n个顶点的连通图的生成树有n-1条边;
- 在生成树中再加一条边必然形成回路。
- 生成树中任意两个顶点间的路径是唯一的。
- 含有n个顶点,n-1条边的图不一定是生成图。
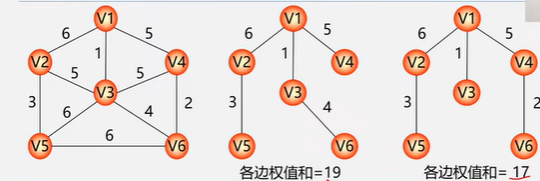
构造最小生成树
构造最小生成树的算法很多,其中多数算法都利用了MST的性质。
MST性质:设N=(V,E)是一个连通网,U是顶点集V的一个非空子集。若边(u,v)是一条具有最小权值的边,其中u∈U,v∈V-U,则必存在一棵树包含边(u,v)的最小生成树。

最小生成树:给定一个无向网络,在该网的所有生成树中,使得各边权值之和最小的那棵树称为该网的最小生成树,也叫做最小代价生成树。