一、图的基本概念

由点（vertices）和边(edges)组成
$G=(V,E)$，$|V|=n$,$|E|=m$ （这里默认有向图，无向图用$G$$=${$V$,$E$}表示

顶点的度是关联在其上的边的数量。满足$\sum degree(v)=2|E|$（握手定理）

路径：一个序列$<V_0,V_1,...,V_k>$且$i=1,2,...,k$满足$(V_{i-1},V_i)$，序列中任意两点之间都是可达的。
简单路径：序列中所有顶点都是不同的。

环：一个路径$<V_0,V_1,...,V_k>$并且$V_0=V_k$并且路径上所有边都是不同的
简单环：$V_1,V_2,...,V_k$是不同的。

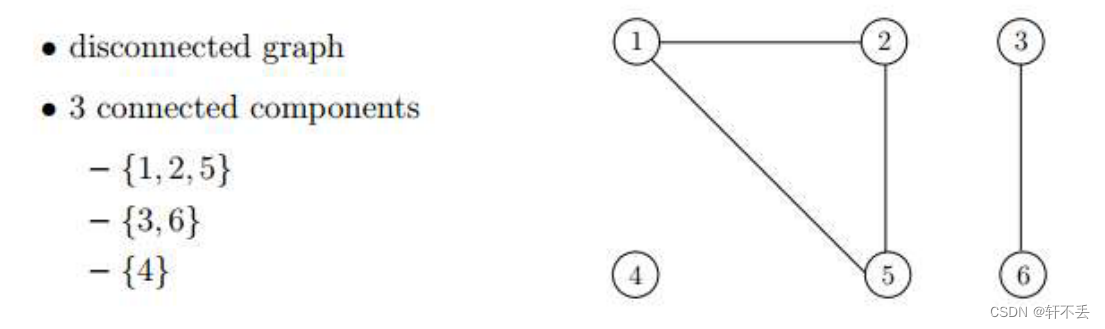
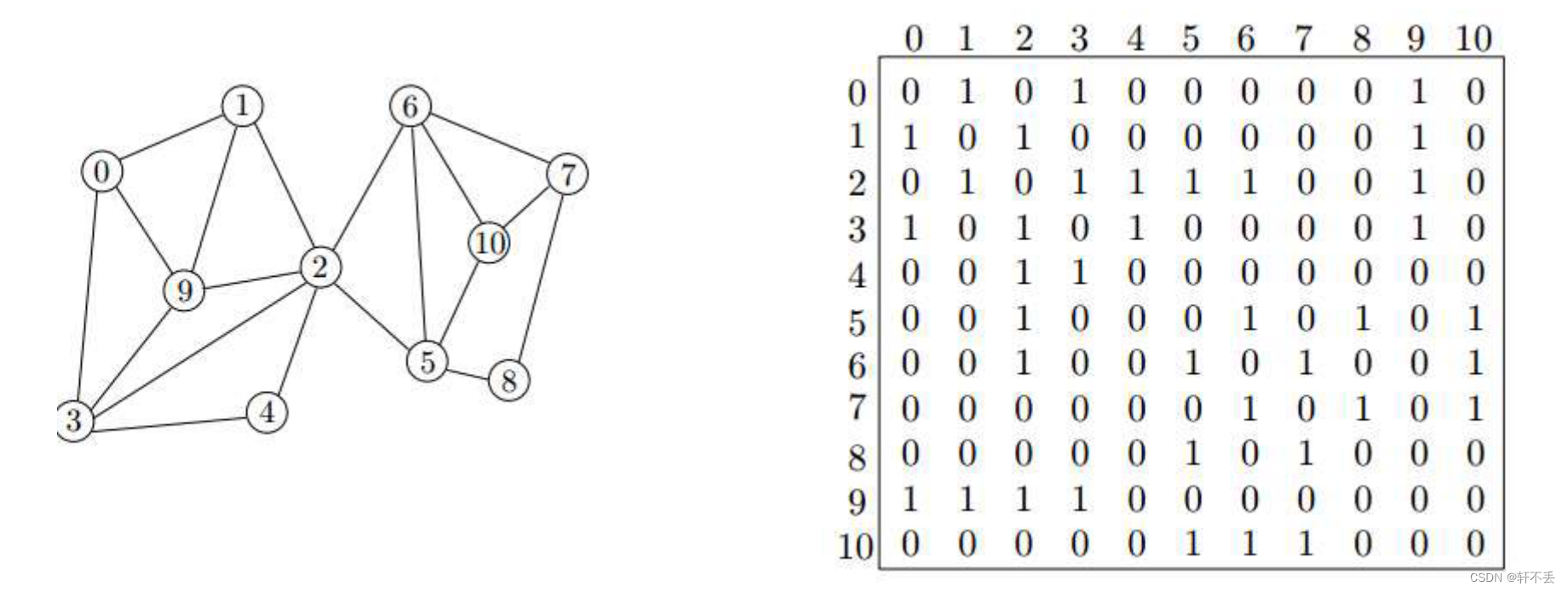
连通：两个点之间存在路径。每个顶点对之间都连通，则这个图是连通的

连通分量：两点之间连通的最大集合的个数（等价类）。如下图：

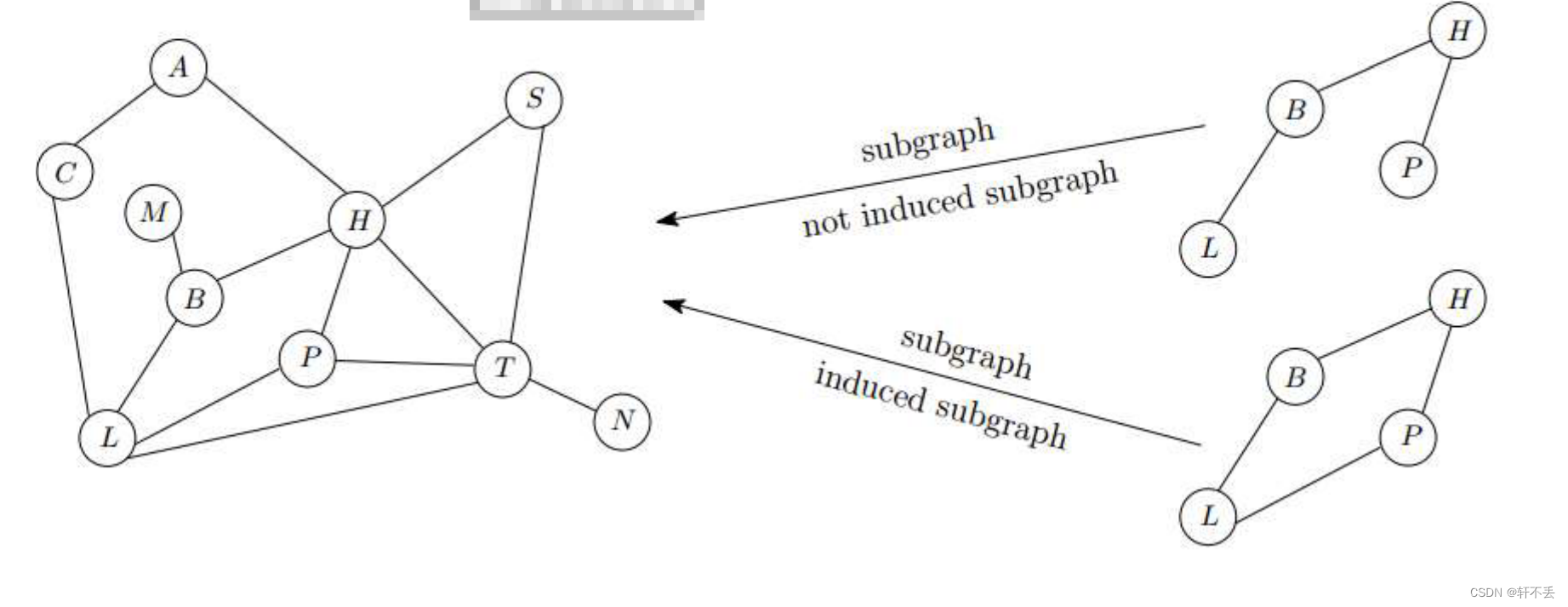
子图：$G^{\prime }$的点和边都属于$G$
诱导子图：$G^{\prime }$的点属于$G$，且连接点的所有边都要属于$G^{\prime }$

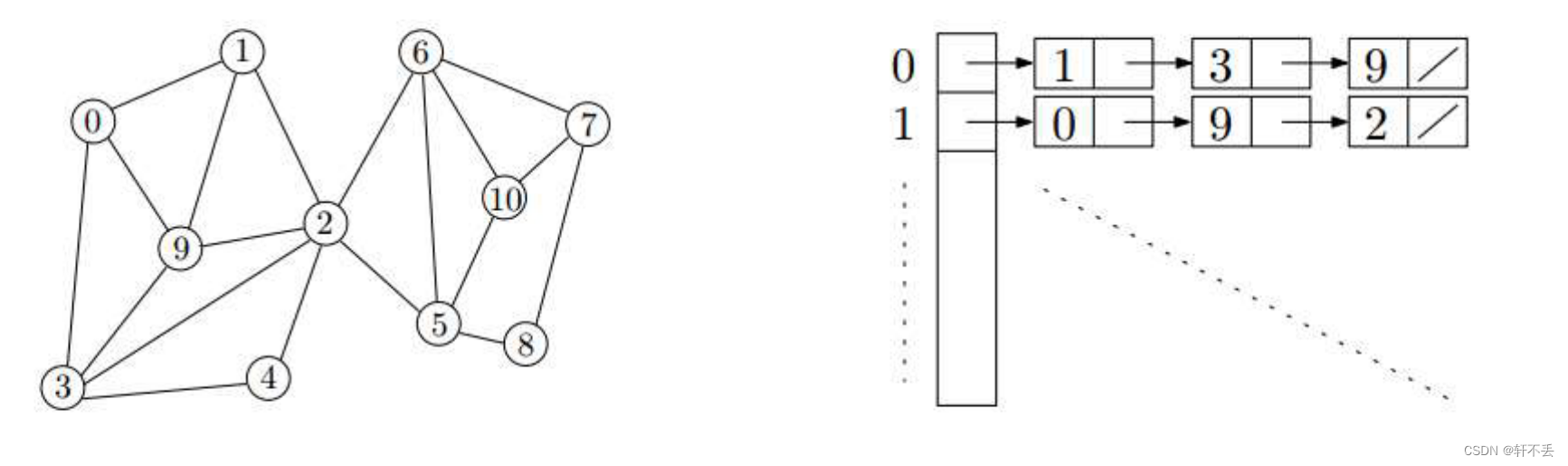
邻接表Adj：用链表连接每个点的边。因此是遍历了每个点和每条边，因此时间复杂度$T(n)=O(V+E)$

邻接矩阵：$A=[a_{ij}],a_{ij}=1$  $if(v_i,v_j)属于E$，否则$a_{ij}=0$
因为不管怎样任意两点间有无边都要判断一遍，因此时间复杂度$T(n)=O(V^2)$

二、广度优先搜索（BFS）

用处：遍历图中的所有顶点，从而显示图的属性

记录

三个数组用于保存遍历期间收集的信息。

1. $color[u]$：访问的每个顶点的颜色
   $WHITE$:未发现
   $GRAY$:已发现但未完成处理
   $BLACK$:已完成处理
2. $pred[u]$：前一个指针：指向发现u的顶点
3. $d[u]$：从源到顶点u的距离

伪代码

BFS(G)
for u in V do
	color[u] ← WHITE;
	pred[u] ← NULL;
end
for u in V do
	if color[u] is equal to WHITE then
		BFSVisit(u);
	end
end

BFSVisit(s)
color[s] ← GRAY,d[s] ← 0;
set Q a queue
Enqueue(Q,s)
while Q is not empty do
	u ← Dequeue(Q)
	for v is belong to Adj[u] do   (邻接表遍历的)
		if(color[v] = WHITE) then
			color[u] ← GRAY
			d[v] ← d[u]+1
			pred[v] ← u
			Enqueue(Q,v)
		end
	end
	color[u] ← BLACK
end

时间复杂度

每一次循环遍历，都是遍历一个点和其边，且边遍历过了其他边就不会再遍历，因此
$T(n)=\sum O(1+degree(u))=O(V+E)$

流程

一次BFSVisit，能将连通分量遍历完

应用

1. 最短路径问题
2. 查找连通分量

三、深度优先搜索（DFS）

用处：同样也是遍历图中的所有顶点，从而显示图的属性

记录

四个数组用于保存遍历期间收集的信息。

1. $color[u]$：访问的每个顶点的颜色
   $WHITE$:未发现
   $GRAY$:已发现但未完成处理
   $BLACK$:已完成处理
2. $pred[u]$：前一个指针：指向发现u的顶点
3. $d[u]$：发现时间。（设置一个全局变量时间发生器）
4. $f[u]$：结束时间。一个计数器，指示顶点u(及其所有后代)的处理何时完成

伪代码

DFS(G)
for u in V do
	color[u] ← WHITE;
	pred[u] ← NULL;
end
 time  ← 0
for u in V do
	if color[u] is equal to WHITE then
		DFSVisit(u);
	end
end

DFSVisit(u)
color[u] ← GRAY,d[u] ← ++time;
set Q a queue
Enqueue(Q,s)
for v is belong to Adj[u] do   (邻接表遍历的)
	if(color[v] = WHITE) then
		pred[v] ← u
		DFSVisit(v)
	end
end
color[u] ← BLACK
f[u] ← ++time;

时间复杂度

同样，每一次循环遍历，都是遍历一个点和其边，且边遍历过了其他边就不会再遍历，因此
$T(n)=\sum O(1+degree(u))=O(V+E)$

流程

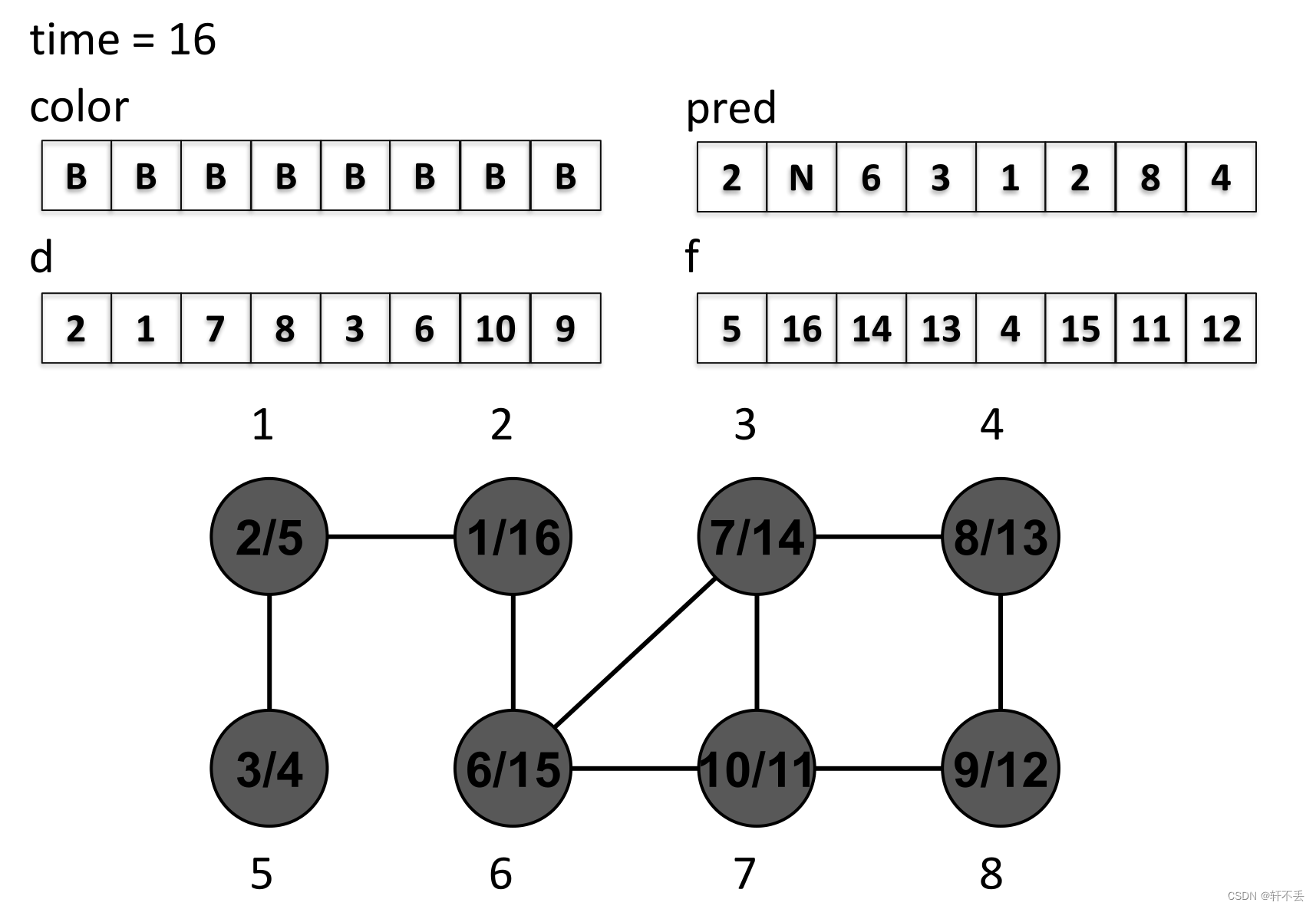
时间戳结构

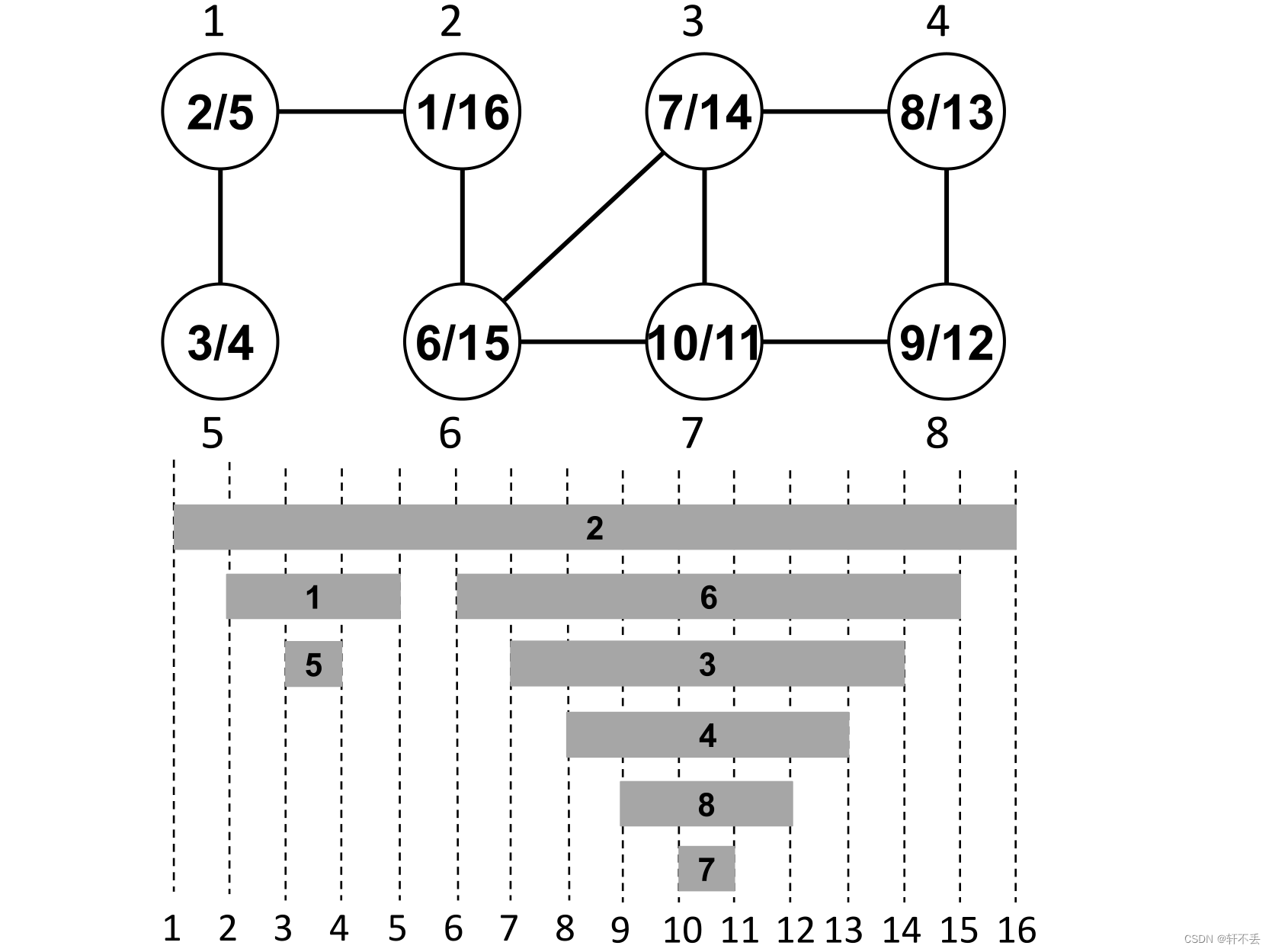
由图可知，$u$是$v$的后代(在$DFS$树中)，当且仅当$[d[u],f[u]]$是$[d[v],f[v]]$的子区间

树边:$if(u,v)\in E_f$等价$u=pred[v]$，即$u$是$DFS$树中$v$的前身(图中蓝色边)
后边缘:如果$v$是$DFS$树中$u$的祖先(不包括前身)（图中红色边）
有边就有祖先和后代的关系

BFS和DFS比较

BFS是发现点之后先处理，DFS是发现点之后不处理，继续往下去找其他的点。

四、拓扑排序

一些概念

有向图

有向图，区分边(u, v)和边(v, u)
顶点的出界度是离开它的边的数量，顶点的入界度是进入它的边的数量
每条边(u, v)对u的出阶贡献1次，对v的入阶贡献1次
$\sum out-degree(v)=\sum in-degree(v)=|E|$

作用

有向图通常用于表示顺序相关的任务，也就是说，我们不能在另一个任务完成之前启动一个任务。
边(u, v)表示任务u完成后才能启动任务v。
显然，要使系统不挂起，图必须是无环的，它必须是有向无环图(或DAG)

拓扑排序

拓扑排序是一种针对有向无环图的算法，对顶点进行线性排序，使得对于DAG中的每条边(u, v)， u在线性排序中出现在v之前。
它可能不是唯一的，因为有许多“不兼容”的元素。

分析

1. 起始顶点入度必须为0，如果这样的顶点不存在，图就不是无环的。
2. 一个入度为0的顶点是一个可以马上开始的任务。所以我们可以先以线性顺序输出它.
3. 如果输出一个顶点u，那么所有的边(u, v)都不再有用，因为任务v不再需要等待u。
4. 去掉顶点u后，新图仍然是一个有向无环图
5. 重复步骤2-4，直到没有顶点留下

伪代码

Initialize Q to be an empty queue
for u is belong to V do then
	if u.in_degree is equal to 0 then
		Enqueue(Q,u)
	end
end
while Q is not empty do
	u ← Dequeue(Q)
	Output u;
	for v is belong to Adj(u) do
		v.in_degree ← v.in_degree-1
		if v,in_degree is equal to 0 then
			Enqueue(Q,v)
		end
	end
end

时间复杂度

依旧是每条边和每个顶点都遍历一遍，因此时间复杂度$T(n)=O(V+E)$

彩蛋

也可用DFS求出拓扑序列，对于每个有向边，都有$f[u]>f[v]$

在时间O(V+E)内计算出$DAG$（有向无环图）中的单源最短路径：动态规划

五、强连通分量-SCC

任意两点之间都有路径，再增加一个点都不满足这个关系。
任何两个强连通分量交集都为空

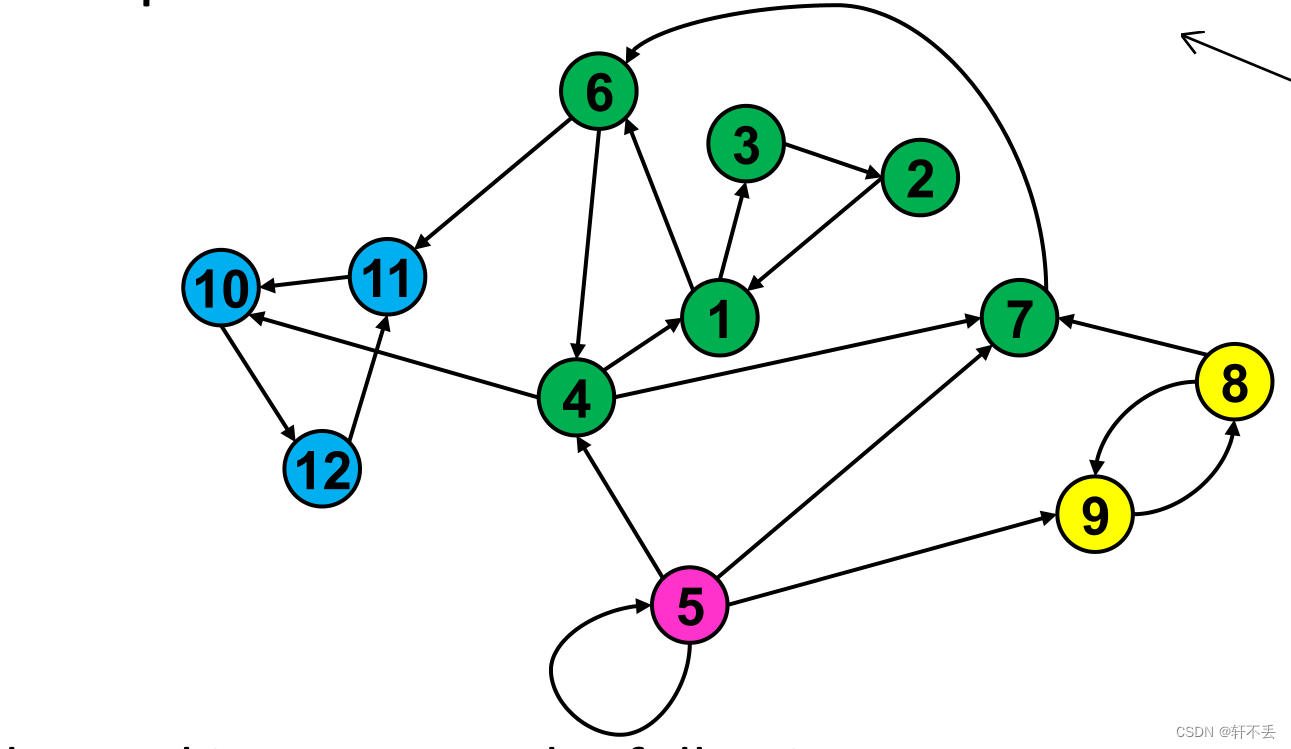
找到一个算法，求一个图得所有连通分量

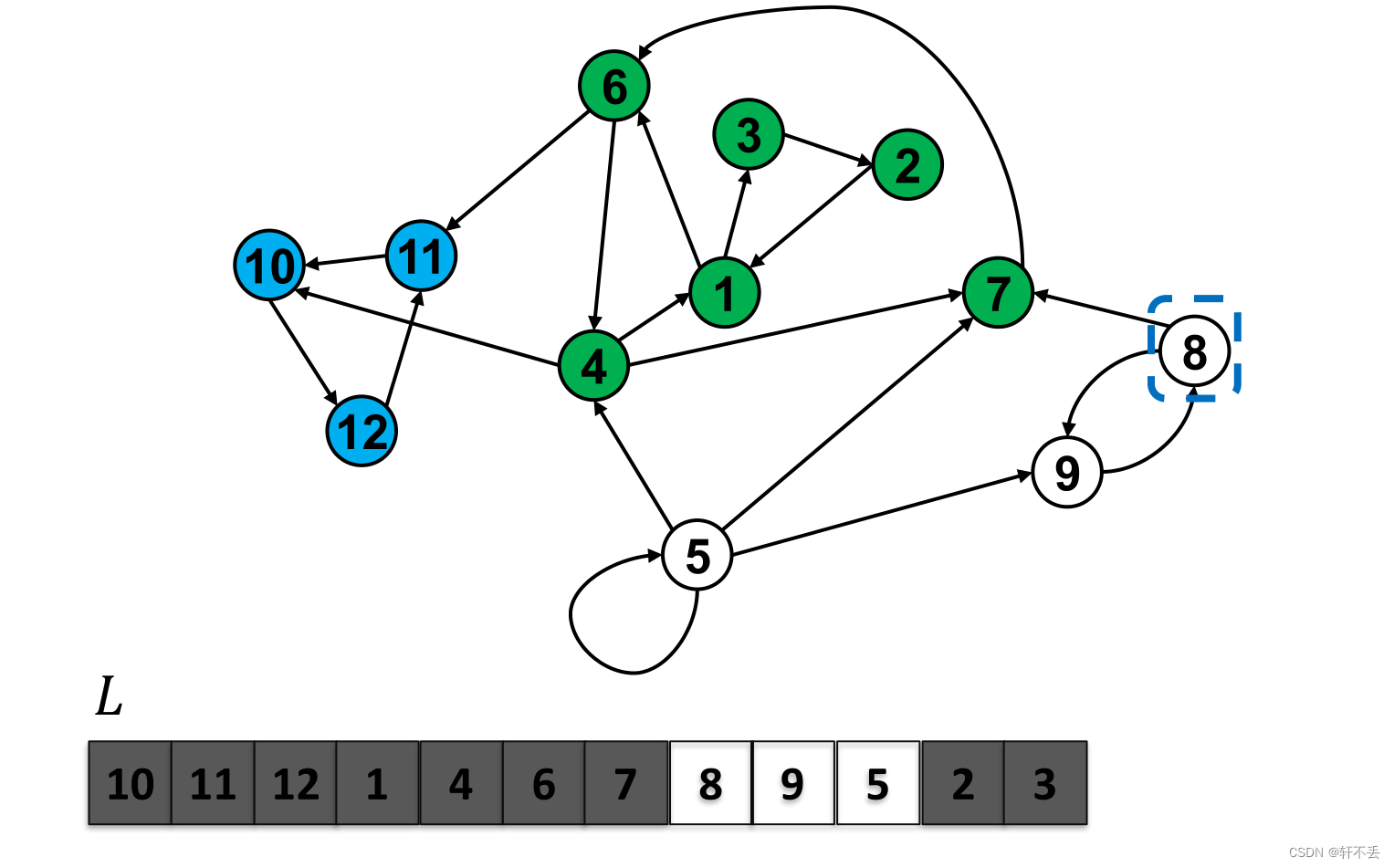
分析

1. 对G中所有边的方向进行反转，得到逆图GR。
2. 执行DFS，并获得GR中顶点变黑的序列，即每当一个顶点从堆栈中弹出时，将其附加到序列$L^R$中，将$L^R$倒序得到序列L
3. 对原图G执行DFS，规则如下
   规则1:从L的第一个顶点开始DFS
   规则2:当需要重新开始时，从L的第一个仍然是白色的顶点开始
   将每个dfs树中的顶点输出为SCC
   

伪代码

R ← {}
Reverse G and get G'
DFS G' and get L'
reverse L' and get L
for u属于L do
	if color[u] is WHITE then
		Lscc ← DFSVisit(G,u)
		R ← RUSet(Lscc)
	end
end

时间复杂度

翻转边需要遍历每个点和边，时间复杂度为$O(V+E)$，DFS时间复杂度为$O(V+E)$,，然后还是依次遍历每个点和边，时间复杂度也是$O(V+E)$，因此总时间复杂度为$T(n)=O(V+E)$