绪论

参考期刊

• ICCV 偏向视觉
• CVPR 偏向ML
• IAAA AI原理
• ICML

参考链接

• CSDN 机器学习知识点全面总结

课堂内容学习-0912-N1

  对于特征提取，简而言之就是同类聚得紧，异类分得开；
  detection研究的是样本二分类问题，即分为正样本和负样本，其中正样本就是我们的检测目标
  对于分类问题就是建立一个特征空间（feature space），寻求空间划分方法，一般而言，对于输入的裸数据，需要对其进行transform,再根据其feature进行特征空间的划分；这里transform就要讲究能将数据很好的根据其特征进行划分。
 划分后的空间特征不是一成不变的，根据所选择的空间基（space basis）的不同，可以得到不同的特征空间，在这里也可以引入稀疏表示（用较少的基本信号的线性组合来表达大部分或者全部的原始信号）

M L = { r e p r e s e n t a t i o n + l o s s _ f u n c t i o n + o p t i m i z e r } l e a r n i n g : s u p e r v i s e d 、 u n s u p e r v i s e d 、 r e i n f o r c e m e n t ML = {\{ representation + loss_\_function + optimizer \}} \\ learning:supervised、unsupervised、reinforcement ML={representation+loss_​function+optimizer}learning:supervised、unsupervised、reinforcement

有监督学习（supervised）

有数据标注情况下学习（回归、分类）
代表算法：决策树、朴素贝叶斯、逻辑回归、KNN、SVM、神经网络、随机森林、AdaBoost、遗传算法；

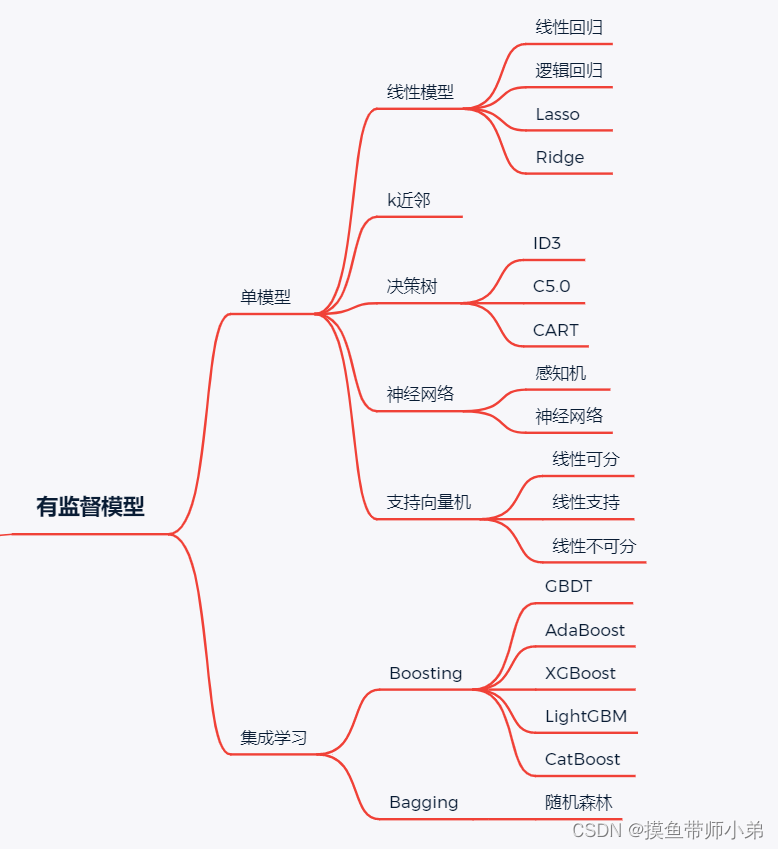
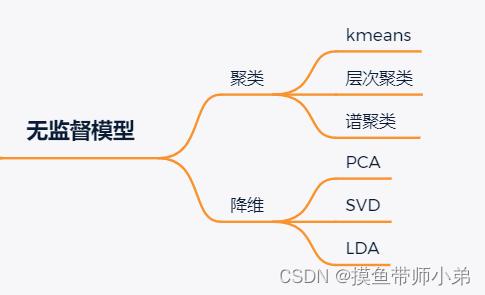
无监督学习

无监督学习主要聚类、维度约减（减少数据的维度同时保证不丢失有意义的信息）
代表算法：主成分分析方法PCA等，等距映射方法、局部线性嵌入方法、拉普拉斯特征映射方法、黑塞局部线性嵌入方法、局部切空间排列方法等；

强化学习

通过学习可以获得最大回报的行为，让agent（个体）根据自己当前的状态，来决定下一步采取的动作，在机器人中应用广泛

补充

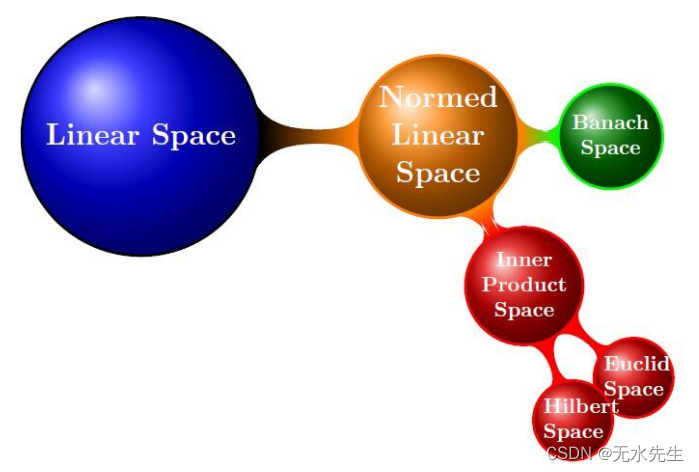
泛函分析

 Functional Analysis (泛函分析)，通俗地，可以理解为微积分从有限维空间到无限维空间的拓展——当然了，它实际上远不止于此。在这个地方，函数以及其所作用的对象之间存在的对偶关系扮演了非常重要的角色。Learning发展至今，也在向无限维延伸——从研究有限维向量的问题到以无限维的函数为研究对象。Kernel Learning 和 Gaussian Process 是其中典型的例子——其中的核心概念都是Kernel。很多做Learning的人把Kernel简单理解为Kernel trick的运用，这就把kernel的意义严重弱化了。在泛函里面，Kernel (Inner Product) 是建立整个博大的代数体系的根本，从metric, transform到spectrum都根源于此

稀疏表示（Sparse representation）

参考链接 https://www.cnblogs.com/yifdu25/p/8128028.html
用较少的基本信号的线性组合来表达大部分或者全部的原始信号。

其中，这些基本信号被称作原子，是从过完备字典中选出来的；而过完备字典则是由个数超过信号维数的原子聚集而来的。可见，任一信号在不同的原子组下有不同的稀疏表示。

假设我们用一个MN的矩阵表示数据集X，每一行代表一个样本，每一列代表样本的一个属性，一般而言，该矩阵是稠密的，即大多数元素不为0。 稀疏表示的含义是，寻找一个系数矩阵A（KN）以及一个字典矩阵B（MK），使得BA尽可能的还原X，且A尽可能的稀疏。A便是X的稀疏表示。

南大周志华老师写的《机器学习》这本书上原文：“为普通稠密表达的样本找到合适的字典，将样本转化为合适的稀疏表达形式，从而使学习任务得以简化，模型复杂度得以降低，通常称为‘字典学习’（dictionary learning），亦称‘稀疏编码’（sparse coding）”块内容。

表达为优化问题的话，字典学习的最简单形式为

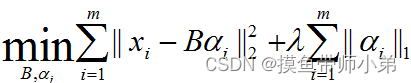
其中xi为第i个样本，B为字典矩阵，αi为xi的稀疏表示，λ为大于0参数。

•寻找少量重要的系数来表示原始信号的技术被称作Sparse Coding（稀疏编码或稀疏分解）；

协方差矩阵

参考链接：如何直观地理解「协方差矩阵」？
参考链接：矩阵特征值和特征向量详细计算过程

方差和协方差的定义

 在统计学中，方差是用来度量单个随机变量的离散程度，而协方差则一般用来刻画两个随机变量的相似程度 ，其中，方差的计算公式为
$${\sigma }_x^2=\frac{1}{n-1}\sum _{i=1}^n(x_i-\bar{x}{)}^2$$
其中，n 表示样本量，符号 $\bar{x}$ 表示观测样本的均值，这个定义在初中阶段就已经开始接触了。
在此基础上，协方差的计算公式被定义为
$$\sigma (x,y)=\frac{1}{n-1}\sum _{i=1}^n(x_i-\bar{x})(y_i-\bar{y})$$
 在上述公式中，符号$\bar{x},\bar{y}$分别表示两个随机变量所对应的观测样本均值,因此，方差 可以看作x关于自己的协方差$\sigma (x,x)$

从方差/协方差到协方差矩阵

 考虑有关的随机变量，给定 $d$ 个随机变量 $x_k,k=1,2,\dots ,d$，则这些随机变量的方差为$$\sigma (x_k,x_k)=\frac{1}{n-1}\sum _{i=1}^n(x_{ki}-{\bar{x}}_k{)}^2,k=1,2,\dots ,d$$
其中，为方便书写，$x_{k}i$ 表示随机变量 $x_k$ 的第 $i$ 个观测值，$n$ 表示样本量，每个随机变量都有对应的观测值个数为 $n$,对于这些随机变量，我们还可以定义其余变量的协方差，实质两两之间的协方差，即
$$\sigma (x_m,x_k)=\frac{1}{n-1}\sum _{i=1}^n(x_{mi}-{\bar{x}}_m)(x_{ki}-{\bar{x}}_k)$$
因此，协方差矩阵为
$$\Sigma =\left[\begin{array}{ccc}\sigma (x_1,x_1)& \cdots & \sigma (x_1,x_d)\\ ⋮& \ddots & ⋮\\ \sigma (x_d,x_1)& \cdots & \sigma (x_d,x_d)\end{array}\right]\in {\mathbb{R}}^{d\times d}$$
其中，对角线上的元素为变量的方差，非对角线上的元素为变量两两之间的协方差，根据协方差的定义，我们可以认定：协方差矩阵是对称矩阵(symmetric matrix)，其大小为 $d\times d$。

从协方差矩阵到相关系数

 相关系数的公式定义如下：
$$\rho =\frac{Cov(X,Y)}{{\sigma }_x{\sigma }_y}$$
对于一个如下一个协方差矩阵，可以求得其对应的相关系数
协方差矩阵为：
$$\left[\begin{array}{ccccc}& 1& -2& -\frac{5}{2}& \\ & -2& 4& 5& \\ & -\frac{5}{2}& 5& 9& \end{array}\right]$$
相关系数为：
$$\left[\begin{array}{ccccc}& 1& -1& -\frac{5}{6}& \\ & -1& 1& \frac{5}{6}& \\ & -\frac{5}{6}& \frac{5}{6}& 1& \end{array}\right]$$

多元正态分布与线性变换

 一个向量 x 服从均值向量为 μ、协方差矩阵为 Σ 的多元正态分布，意味着这个向量的每一个分量都有其自己的均值和方差，这些参数描述了变量之间的关系以及它们各自的波动性，而整个向量则满足多元正态分布。

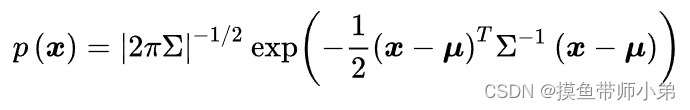
 均值向量 μ 描述了向量的每个分量的平均值,也即${\mu }_i$描述的是第i个分量的平均值
 协方差矩阵 Σ 描述了向量中各个分量之间的相关性以及它们各自的方差
因此，向量在各个分量上的平均值是${\mu }_i$，第$i$个分量的方差是${\sigma }_i$，第$i$个与第$j$个分量之间的协方差是${\sigma }_{ij}$