一、解决XOR问题

1. 回顾XOR问题：

        如图，如何对XOR面进行分割以划分四个输入  对应的输出  呢？

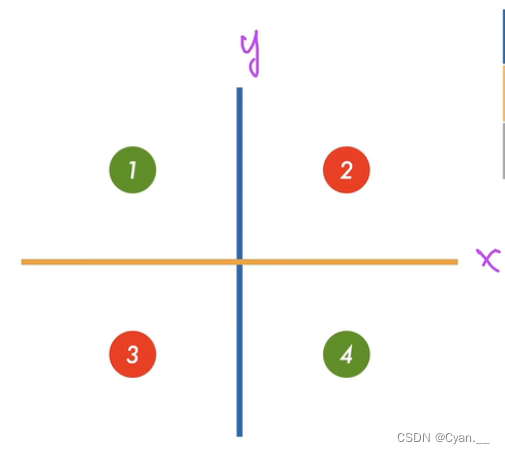
· 思路：采用两个分类器分类，每次分出两个输入 ，再借助这两个分类从而分出 。

        即采用同或运算，当两次分类的值相同时，输出为1；当两次分类的值不同时，输出为0.

        · 蓝色的线将1、3赋值1，2、4赋值0，从而分隔开；黄色的线将1、2赋值1，3、4赋值0；

        · 那么，如果两次赋值相同，即表示它们是第一类；不同表示他们是第二类，由此分类。

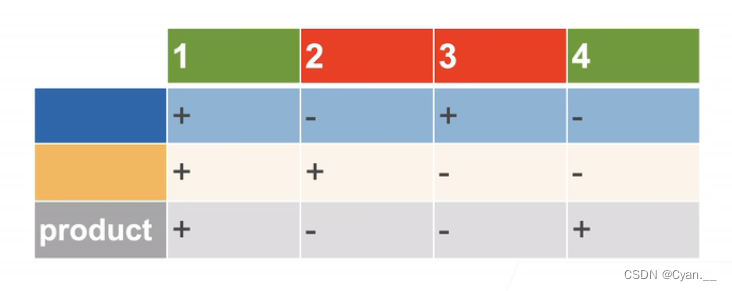
2. 如何利用感知机解决XOR问题

由上述原理可得，既然一层感知机无法处理XOR问题分类，那么可以用多个感知机函数来进行处理。用好几层分类多次，最后对之前的分类结果求和取一个算法，就得到了最终的分类结果。

二、多层感知机的代码实现

代码：

import torch
from torch import nn
from d2l import torch as d2l
# 继续使用fashion_mnist数据集进行分类操作，定义小批量数据
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

# 每张图片为28x28=784像素值，可看作784个特征值的具有10个类别的分类数据集
# 首先实现一个具有单隐藏层的多层感知机，包含256个隐藏单元，有输入->隐藏->输出三层
# W1: 输入层到隐藏层的权重矩阵，大小为 (num_inputs, num_hiddens)
# b1: 隐藏层的偏置项，大小为 (num_hiddens,)
# W2: 隐藏层到输出层的权重矩阵，大小为 (num_hiddens, num_outputs)
# b2: 输出层的偏置项，大小为 (num_outputs,)
# nn.Parameter 表示这些变量是模型参数，需要在训练过程中进行更新
# 乘以 0.01 是为了缩小初始化值的范围，有助于训练的稳定性
num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = nn.Parameter(torch.randn(
    num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
    num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

# 实现ReLU激活函数，返回max(0, x)
def relu(X):
    a = torch.zeros_like(X)
    return torch.max(X, a)

# 实现模型，将输入的二维图像转化为一个一维向量，长度为num_inputs
def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(X@W1 + b1)  # 这里“@”代表矩阵乘法
    return (H@W2 + b2)

# 实现损失函数
# 由于实现了softmax损失函数，使得不必在输出层调用sigmoid激活函数将输出值收缩到概率区间
# Softmax激活函数是sigmoid的推广，用于多分类问题的输出层。它会将输出归一化为概率分布，使得所有类别的预测概率总和为1
loss = nn.CrossEntropyLoss(reduction='none')

# 训练模型，迭代10个周期，学习率设定为0.1
num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

# 应用模型进行测试与评估
d2l.predict_ch3(net, test_iter)