代码随想录-刷题第二天

news2024/9/22 23:20:48

977. 有序数组的平方

题目链接：977. 有序数组的平方

思路：双指针思想，数组是有序的且含有负数，其中元素的平方一定是两边最大。定义两个指针，从两端开始向中间靠近，每次比较两个指针的元素平方大小，将较大的一个存入结果数组。（注意结果数组是从小到大的，所以要从后往前开始存入）

时间复杂度：O(n)，空间复杂度O(n)

class Solution {
    public int[] sortedSquares(int[] nums) {
        int n = nums.length;
        // 两个指针分别初始化在正负子数组绝对值最大的元素索引
        int i = 0, j = n - 1;
        // 得到的有序结果是降序的
        int p = n - 1;
        int[] res = new int[n];
        // 执行双指针合并有序数组的逻辑
        // 注意这里要i <= j，因为最后要处理两个元素
        while (i <= j) {
            if (Math.abs(nums[i]) > Math.abs(nums[j])) {
                res[p] = nums[i] * nums[i];
                i++;
            } else {
                res[p] = nums[j] * nums[j];
                j--;
            }
            p--;
        }
        return res;
    }
}

也可以使用for循环写法

public int[] sortedSquares(int[] nums) {
    int left = 0, right = nums.length - 1;
    int[] res = new int[nums.length];
    int p = res.length - 1;
    for (int i = 0; i < res.length; i++) {
        if (nums[left] * nums[left] > nums[right] * nums[right]){
            res[p] = nums[left] * nums[left];
            left++;
        }else {
            res[p] = nums[right] * nums[right];
            right--;
        }
        p--;
    }
    return res;
}

209. 长度最小的子数组

题目链接：209. 长度最小的子数组

思路：滑动窗口，两个指针代表窗口的左右边界，右边界一直遍历到最后，当窗口中元素和大于目标值的时候，更新结果，并且左边界往前走一步。（注意：这里一定是窗口右边界遍历一次，然后根据条件更新左边界。如果左边界作为遍历条件，一次循环是解不出来的。）

时间复杂度：O(n)

为什么时间复杂度是O(n) ?

不要以为双重while就是O(n^2)啊，主要是看每一个元素被操作的次数，每个元素在滑动窗口进来操作一次，出去操作一次，每个元素都是被操作两次，所以时间复杂度是 2 × n 也就是O(n)。

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int i = 0;    // i代表窗口左边界
        int j = 0;    // j为窗口右边界
        int res = nums.length + 1;    // 定义结果为最大
        int total = 0;     // total存放窗口中元素和
        while (j < nums.length) {
            total = total + nums[j];
            j++;
            // 窗口中元素符合题意，更新结果，更新左边界和total
            while (total >= target) {
                res = Math.min(res, j - i);
                total = total - nums[i];
                i++;
            }
        }
        return res == nums.length + 1 ? 0 : res;
    }
}

59. 螺旋矩阵II

题目链接：59. 螺旋矩阵II

思路：本题并不涉及什么算法，就是模拟过程，但却十分考察对代码的掌控能力。借用代码随想录中的图片容易理解。注意每次只需要改变二维数组行或列的坐标。

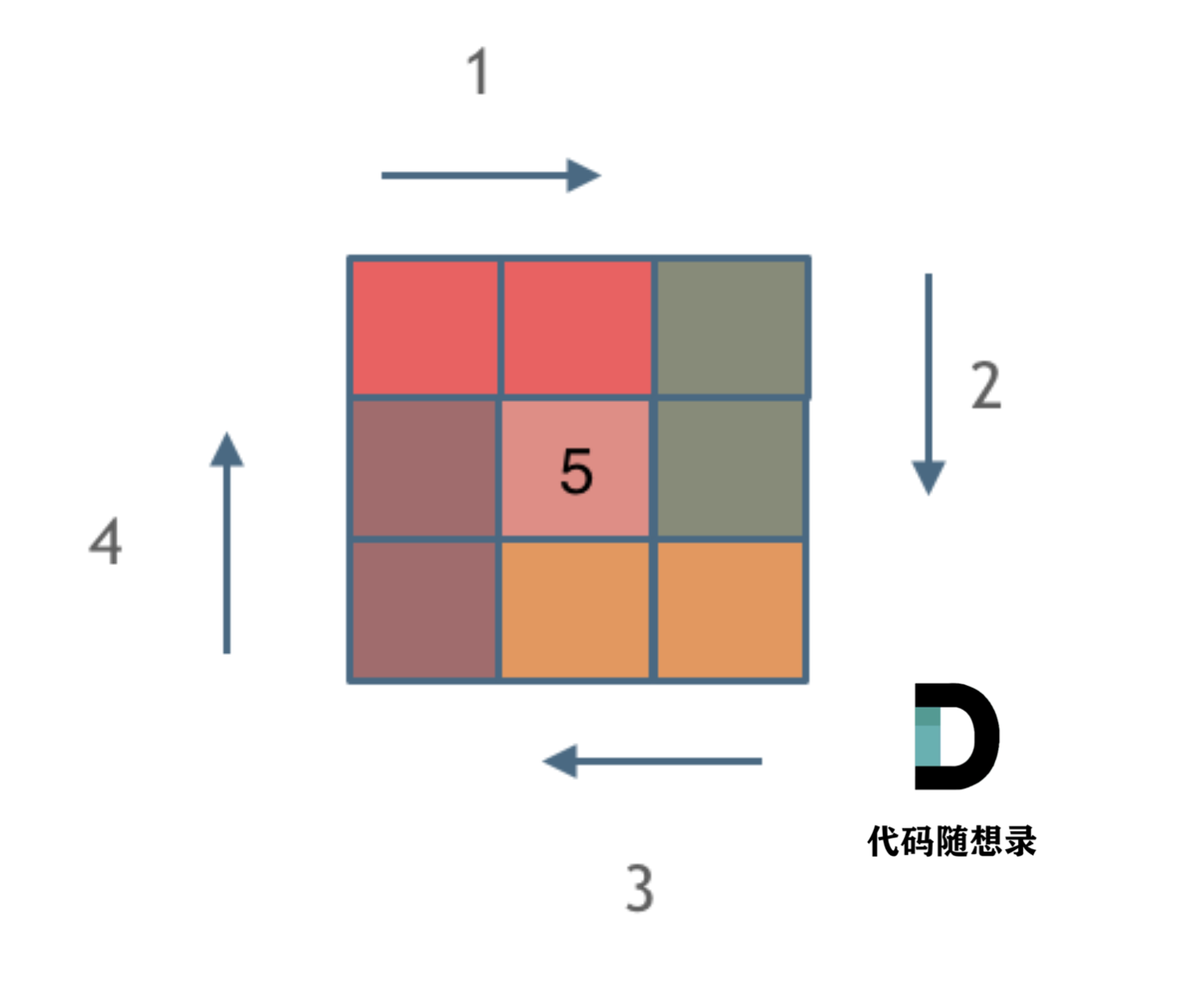
时间复杂度：O(n)

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] matrix = new int[n][n];
        int upper_bound = 0, lower_bound = n - 1;
        int left_bound = 0, right_bound = n - 1;
        // 需要填入矩阵的数字
        int num = 1;
        
        while (num <= n * n) {
            if (upper_bound <= lower_bound) {
                // 在顶部从左向右遍历
                for (int j = left_bound; j <= right_bound; j++) {
                    matrix[upper_bound][j] = num++;
                }
                // 上边界下移
                upper_bound++;
            }
            
            if (left_bound <= right_bound) {
                // 在右侧从上向下遍历
                for (int i = upper_bound; i <= lower_bound; i++) {
                    matrix[i][right_bound] = num++;
                }
                // 右边界左移
                right_bound--;
            }
            
            if (upper_bound <= lower_bound) {
                // 在底部从右向左遍历
                for (int j = right_bound; j >= left_bound; j--) {
                    matrix[lower_bound][j] = num++;
                }
                // 下边界上移
                lower_bound--;
            }
            
            if (left_bound <= right_bound) {
                // 在左侧从下向上遍历
                for (int i = lower_bound; i >= upper_bound; i--) {
                    matrix[i][left_bound] = num++;
                }
                // 左边界右移
                left_bound++;
            }
        }
        return matrix;
    }
}