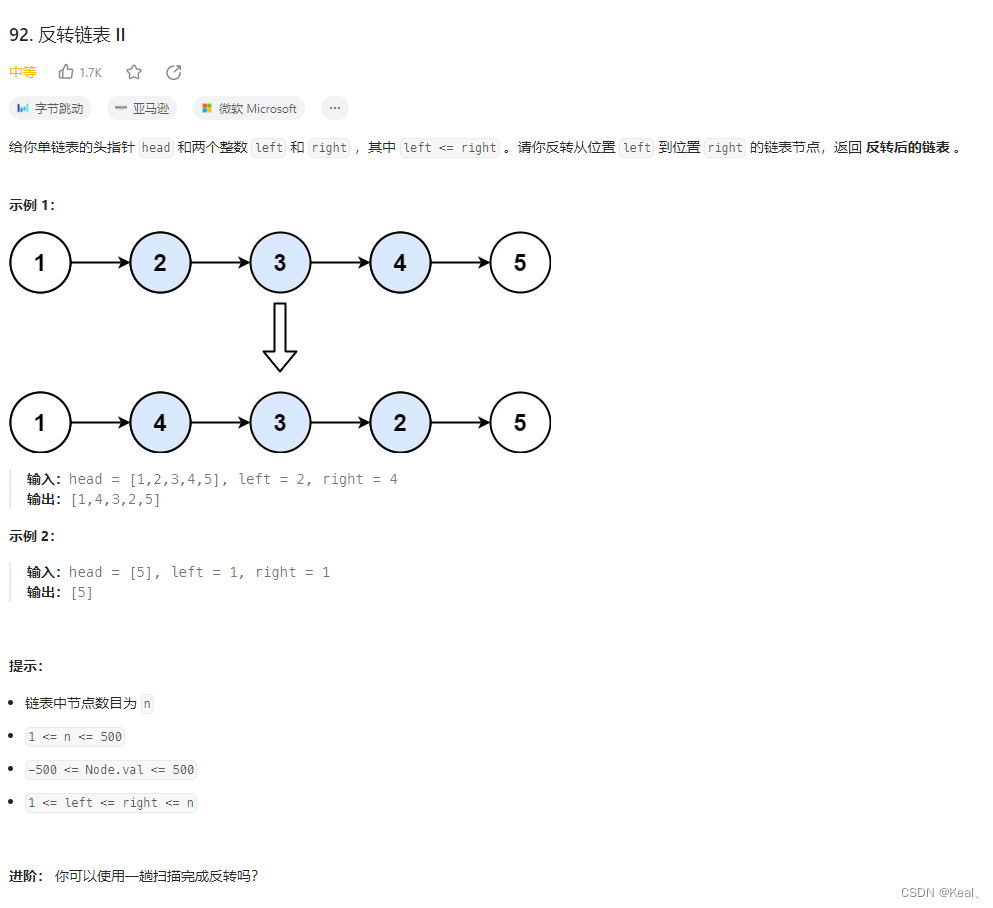
文章目录
- 怪盗基德的滑翔翼
- 登山
- 合唱队形
- 友好城市
- 最大上升子序列和
- 拦截导弹
- 导弹防御系统
- 最长公共上升子序列
一、怪盗基德的滑翔翼OJ链接
本题思路:本题是上升子序列模型中比较简单的模型,分别是从前往后和从后往前走一遍LIS即可。
#include <bits/stdc++.h>
constexpr int N=110;
int n;
int h[N];
int f[N];
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);std::cout.tie(nullptr);
int T;
std::cin>>T;
while(T--){
std::cin>>n;
for(int i=1;i<=n;i++) std::cin>>h[i];
int res=0;
//正向求解LIS问题
for(int i=1;i<=n;i++){
f[i]=1;
for(int j=1;j<i;j++)
if(h[j]<h[i]) f[i]=std::max(f[i],f[j]+1);
res=std::max(f[i],res);
}
memset(f,0,sizeof f);//这里需要将此时的f数组进行清零处理
//反向求解LIS问题
for(int i=n;i>=1;i--){
f[i]=1;
for(int j=n;j>i;j--)
if(h[j]<h[i]) f[i]=std::max(f[i],f[j]+1);
res=std::max(f[i],res);
}
std::cout<<res<<std::endl;
}
return 0;
}二、登山OJ链接
本题思路:状态表示f[i]表示以第 i个位置作为当前子序列的右端点的值,g[i]表示以第 i
个位置作为当前子序列的左端点的值。状态属性:f[i]求最长上升子序列的最多景点个数,g[i]求最长下降子序列的最多景点个数。状态计算:f[i]=max(f[i],f[j]+1)(1≤j<i≤n),g[i]=max(g[i],g[j]+1)(1≤i<j≤n)
求新数组最长上升子序列就是求原数组最长下降子序列答案表示:根据每一个点来划分:ans=max(包含 i的最长上升子序列 + 包含 i的最长下降子序列)所以 ans=max(f[i]+g[i]−1)。
#include <bits/stdc++.h>
constexpr int N=1010;
int n;
int h[N];
int f[N],g[N];//f用来表示上升子序列 g表示下降子序列
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);std::cout.tie(nullptr);
std::cin>>n;
for(int i=1;i<=n;i++) std::cin>>h[i];
for(int i=1;i<=n;i++){//求出上升子序列
f[i]=1;
for(int j=1;j<i;j++)
if(h[j]<h[i])
f[i]=std::max(f[i],f[j]+1);
}
for(int i=n;i>=1;i--){//求出下降子序列
g[i]=1;
for(int j=n;j>i;j--)
if(h[j]<h[i])
g[i]=std::max(g[i],g[j]+1);
}
int res=0;
for(int i=1;i<=n;i++)
res=std::max(res,f[i]+g[i]-1);
std::cout<<res<<std::endl;
return 0;
}三、合唱队形OJ链接
本题思路:本题与上面一题差不多。
#include <bits/stdc++.h>
constexpr int N=1010;
int n;
int h[N];
int f[N],g[N];
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);std::cout.tie(nullptr);
std::cin>>n;
for(int i=1;i<=n;i++) std::cin>>h[i];
for(int i=1;i<=n;i++){
f[i]=1;
for(int j=1;j<i;j++)
if(h[j]<h[i])
f[i]=std::max(f[i],f[j]+1);
}
for(int i=n;i>=1;i--){
g[i]=1;
for(int j=n;j>i;j--)
if(h[j]<h[i])
g[i]=std::max(g[i],g[j]+1);
}
int res=0;
for(int i=1;i<=n;i++) res=std::max(res,f[i]+g[i]-1);
std::cout<<n-res<<std::endl;
return 0;
}四、友好城市OJ链接
本题思路:这里的我们可以先想想交叉和不交叉的情况下分别画出来的图是什么样子的。我们可以发现,在两座桥不交叉的情况下,有a1<a2,b1<b2,在两座桥相交的情况下,有a1<a2,b2<b1所以我们可以发现两桥是否交叉是可以用北岸城市编号的大小关系给反应出来的。所以我们的思路就可以转化为以南岸的城市编号为基准,把所有的城市对从小到大排序,从而得到关于北岸城市的一个数组。因为当bi<bj时能成功建一座桥,所以问题就转化成了求取这个数组的最长上升子序列。到此,我们对北方城市的数组做一次 LIS就可以得到答案了。
#include <bits/stdc++.h>
#define x first
#define y second
typedef std::pair<int, int> PII;
constexpr int N=5010;
int n;
int f[N];
PII line[N];
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);std::cout.tie(nullptr);
std::cin>>n;
for(int i=1;i<=n;i++)
std::cin>>line[i].x>>line[i].y;
std::sort(line+1,line+n+1);
int res=0;
for(int i=1;i<=n;i++){
for(int j=0;j<i;j++)
if(line[j].y<line[i].y)
f[i]=std::max(f[i],f[j]+1);
res=std::max(res,f[i]);
}
std::cout<<res<<std::endl;
return 0;
}