背包问题
01背包
每个物品只能放一次
2. 01背包问题 - AcWing题库
二维dp
#include<bits/stdc++.h>
const int N=1010;
int f[N][N];
int v[N],w[N];
signed main()
{
int n,m;
std::cin>>n>>m;
for(int i=1;i<=n;i++) std::cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
f[i][j]=f[i-1][j];
if(j>=v[i]) f[i][j]=std::max(f[i][j],f[i-1][j-v[i]]+w[i]);
}
}
std::cout<<f[n][m];
return 0;
}一维dp
观察上面的循环内的式子,发现推导出f[i][j]只需要f[i-1][j]和f[i-1][j-v[i]]就好,也就是当前的f[i]是由上一层f[i-1]推导而来,因此我们用到滚动数组来对二维dp进行优化。
滚动数组是一种优化算法技巧,常用于动态规划问题中,用来减少空间复杂度。在动态规划问题中,我们通常需要使用一个数组来存储中间计算的结果,以供后续计算使用。而滚动数组通过利用数组中的部分空间,不断覆盖原来的值,从而减少所使用的空间。
具体来说,滚动数组通常用一个较小的大小来表示原数组,这个较小的大小是经过推导和分析所确定的。在计算过程中,我们只需要维护这个较小的数组,当需要用到原数组中的值时,通过计算得到。
这种技巧能够在一定程度上减少使用的空间复杂度,特别是针对一些状态转移方程只与之前的一部分状态有关的情况。滚动数组在动态规划问题中被广泛应用,能够提高算法的效率。
同时, 原循环中f[i][j]=std::max(f[i][j],f[i-1][j-v[i]]+w[i]);,如果j是正序即从v[i]-m,那么这里的f[j-v[i]]就是f[i][j-v[i]],因为在循环中正序从小到大会覆盖掉之前的f[i-1],故而采取逆序。滚动数组(简单说明)_滚动数组思想-CSDN博客
#include<bits/stdc++.h>
const int N=1010;
int f[N];
int v[N],w[N];
signed main()
{
int n,m;
std::cin>>n>>m;
for(int i=1;i<=n;i++) std::cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
{
for(int j=m;j>=v[i];j--)
{
f[j]=std::max(f[j],f[j-v[i]]+w[i]);
}
}
std::cout<<f[m];
return 0;
}完全背包
物品有无限件
3. 完全背包问题 - AcWing题库
三重循环
额外加一层循环来枚举选择当前项的个数,这样会超时
#include<bits/stdc++.h>
const int N=1010;
int f[N][N];
int v[N],w[N];
signed main()
{
int n,m;
std::cin>>n>>m;
for(int i=1;i<=n;i++) std::cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
for(int k=0;k*v[i]<=j;k++)
{
f[i][j]=std::max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
}
}
}
std::cout<<f[n][m];
return 0;
}二重循环
与01背包不同的是max里面是f[i][j-v[i]]+w[i],01背包中这里是 f[i-1][j-v[i]]+w[i]
因此下面优化成一维时对j的枚举按升序就好。
#include<bits/stdc++.h>
const int N=1010;
int f[N][N];
int v[N],w[N];
signed main()
{
int n,m;
std::cin>>n>>m;
for(int i=1;i<=n;i++) std::cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
f[i][j]=f[i-1][j];
if(j>=v[i]) f[i][j]=std::max(f[i][j],f[i][j-v[i]]+w[i]);
}
}
std::cout<<f[n][m];
return 0;
}一维循环
#include<bits/stdc++.h>
const int N=1010;
int f[N];
int v[N],w[N];
signed main()
{
int n,m;
std::cin>>n>>m;
for(int i=1;i<=n;i++) std::cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
{
for(int j=v[i];j<=m;j++)
{
f[j]=std::max(f[j],f[j-v[i]]+w[i]);
}
}
std::cout<<f[m];
return 0;
}多重背包问题
物品只有s[i]件
4. 多重背包问题 I - AcWing题库
三重循环
#include<bits/stdc++.h>
const int N=1e3+10;
int v[N],w[N],s[N];
int num,val;
int f[N][N];//从前i件中选,剩余容量为
signed main()
{
std::cin>>num>>val;
for(int i=1;i<=num;i++) std::cin>>v[i]>>w[i]>>s[i];
for(int i=1;i<=num;i++)//枚举物品
{
for(int j=0;j<=val;j++)
{
for(int k=0;k*v[i]<=j&&k<=s[i];k++)
{
f[i][j]=std::max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
}
}
}
std::cout<<f[num][val];
return 0;
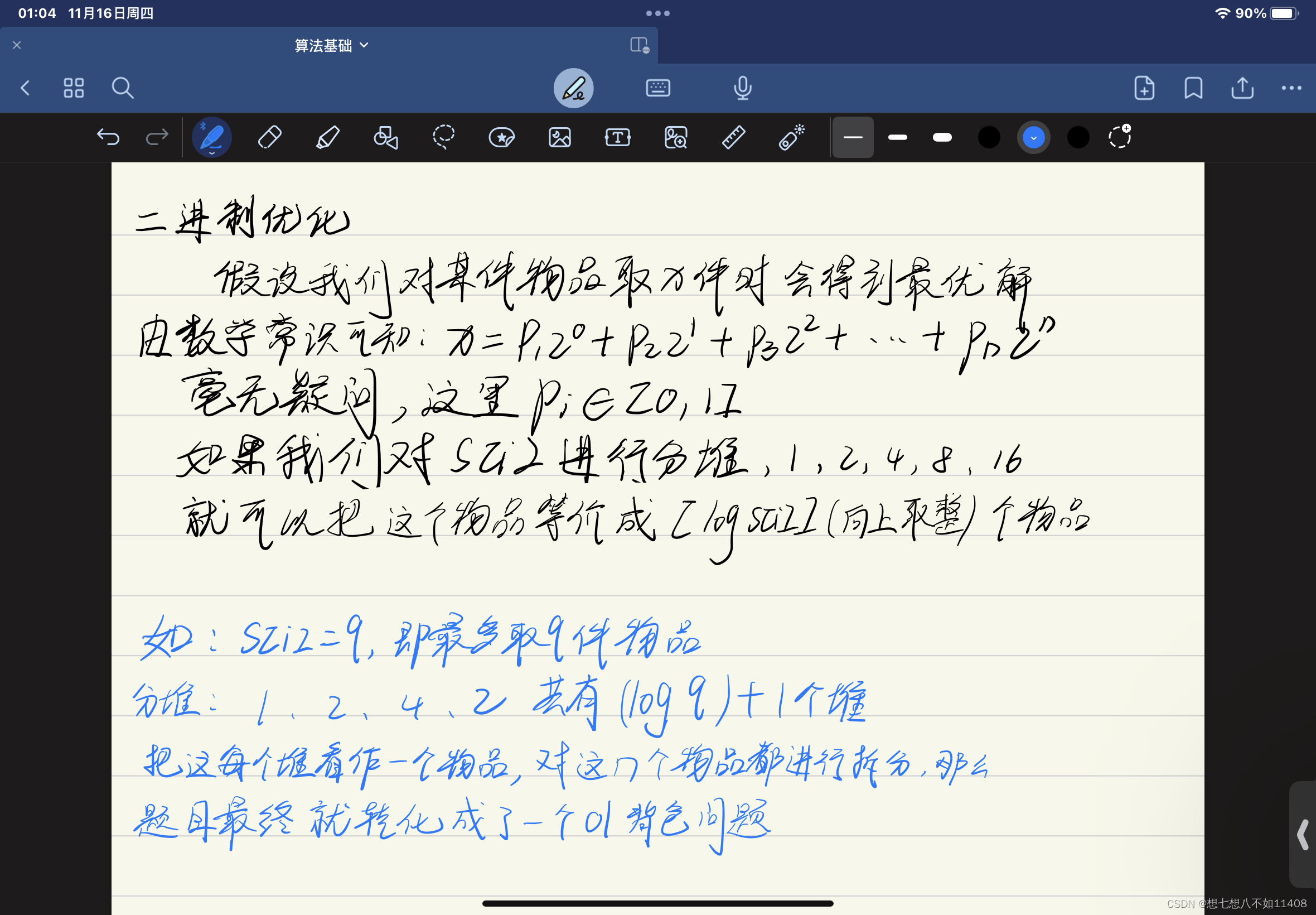
}二进制优化
5. 多重背包问题 II - AcWing题库
#include<bits/stdc++.h>
const int N = 12010, M = 2010;
int v[N], w[N];
int f[M];
int num,val,cnt;
signed main()
{
std::cin>>num>>val;
for(int i=1;i<=num;i++)
{
int a,b,s;
std::cin>>a>>b>>s;
int k=1;
while(s>=k)
{
cnt++;
v[cnt]=a*k;
w[cnt]=b*k;
s-=k;
k*=2;
}
if(s)
{
cnt++;
v[cnt]=a*s;
w[cnt]=b*s;
}
}
for(int i=1;i<=cnt;i++)
{
for(int j=val;j>=v[i];j--)
{
f[j]=std::max(f[j],f[j-v[i]]+w[i]);
}
}
std::cout<<f[val];
return 0;
}分组背包问题
9. 分组背包问题 - AcWing题库
每组物品有若干个,同一组内的物品最多只能选一个。
二维dp
#include<bits/stdc++.h>
const int N=110;
int s[N],w[N][N],v[N][N],f[N][N];
int num,val;
signed main()
{
std::cin>>num>>val;//组数
for(int i=1;i<=num;i++)
{
std::cin>>s[i];
for(int j=1;j<=s[i];j++)
{
std::cin>>v[i][j]>>w[i][j];
}
}
for(int i=1;i<=num;i++)
{
for(int j=0;j<=val;j++)
{
f[i][j]=f[i-1][j];
for(int k=0;k<=s[i];k++)
{
if(j>=v[i][k]) f[i][j]=std::max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);
}
}
}
std::cout<<f[num][val];
return 0;
}一维dp
#include<bits/stdc++.h>
const int N=110;
int s[N],w[N][N],v[N][N],f[N];
int num,val;
signed main()
{
std::cin>>num>>val;//组数
for(int i=1;i<=num;i++)
{
std::cin>>s[i];
for(int j=1;j<=s[i];j++)
{
std::cin>>v[i][j]>>w[i][j];
}
}
for(int i=1;i<=num;i++)
{
for(int j=val;j>=0;j--)
{
for(int k=1;k<=s[i];k++)
{
if(j>=v[i][k]) f[j]=std::max(f[j],f[j-v[i][k]]+w[i][k]);
}
}
}
std::cout<<f[val];
return 0;
}线性DP
数字三角形
898. 数字三角形 - AcWing题库

#include<bits/stdc++.h>
const int N=510;
int f[N][N],a[N][N];
signed main()
{
int n;
std::cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++) std::cin>>a[i][j];
}
for(int i=n;i>=1;i--)
{
for(int j=1;j<=i;j++)
{
f[i][j]=std::max(f[i+1][j],f[i+1][j+1])+a[i][j];
}
}
std::cout<<f[1][1];
return 0;
}最长上升子序列
双重循环
895. 最长上升子序列 - AcWing题库
#include<bits/stdc++.h>
const int N=1e3+10;
int a[N],f[N];
signed main()
{
int n;
std::cin>>n;
for(int i=1;i<=n;i++) std::cin>>a[i];
for(int i=1;i<=n;i++)
{
f[i]=1;
for(int j=1;j<i;j++)
{
if(a[j]<a[i]) f[i]=std::max(f[i],f[j]+1);
}
}
int res=-1e9;
for(int i=1;i<=n;i++) res=std::max(res,f[i]);
std::cout<<res;
return 0;
}优化

#include<bits/stdc++.h>
const int N=1e3+10;
int a[N],q[N];
int n,cnt;
signed main()
{
std::cin>>n;
for(int i=1;i<=n;i++) std::cin>>a[i];
for(int i=1;i<=n;i++)
{
if(a[i]>q[cnt]||!cnt) q[++cnt]=a[i];//q从1开始
else{
int l=1,r=cnt,res=-1;
while(l<=r)
{
int mid=l+r>>1;
if(q[mid]>=a[i])
{
res=mid;
r=mid-1;
}else l=mid+1;
}
q[res]=a[i];
}
}
std::cout<<cnt;
return 0;
}最长公共子序列
897. 最长公共子序列 - AcWing题库
#include<bits/stdc++.h>
const int N=1e3+10;
char a[N],b[N];
int n,m;
int f[N][N];
signed main()
{
std::cin>>n>>m;
std::cin>>a+1>>b+1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
f[i][j]=std::max(f[i-1][j],f[i][j-1]);
if(a[i]==b[j]) f[i][j]=std::max(f[i][j],f[i-1][j-1]+1);
}
}
std::cout<<f[n][m];
return 0;
}最短编辑距离
902. 最短编辑距离 - AcWing题库
#include<bits/stdc++.h>
const int N=1e3+10;
char a[N],b[N];
int n,m;
int f[N][N];
signed main()
{
std::cin>>n>>a+1>>m>>b+1;
for(int i=0;i<=n;i++) f[i][0]=i;
for(int j=0;j<=m;j++) f[0][j]=j;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
f[i][j]=std::min(f[i-1][j],f[i][j-1])+1;//增,删的情况
if(a[i]==b[j]) f[i][j]=std::min(f[i][j],f[i-1][j-1]);
else f[i][j]=std::min(f[i][j],f[i-1][j-1]+1);//判断是否需要改
}
}
std::cout<<f[n][m];
return 0;
}编辑距离
899. 编辑距离 - AcWing题库
给定n个字符串,m次询问每次给一个字符串和限制,问每次询问中n个字符串中每次有多少个可以在操作限制内改为给的字符
这里发现f数组中,前面是枚举给定字符串还是要修改的字符串不会影响答案。
#include<bits/stdc++.h>
const int N=1e3+10;
int n,m;
char s[N][15];
int f[N][N];
/*
int dis(char a[],char s[])//把s变成a
{
int la=strlen(a+1),ls=strlen(s+1);
for(int i=0;i<=la;i++) f[i][0]=i;
for(int i=0;i<=ls;i++) f[0][i]=i;
for(int i=1;i<=la;i++)
{
for(int j=1;j<=ls;j++)
{
f[i][j]=std::min(std::min(f[i-1][j]+1,f[i][j-1]+1),f[i-1][j-1]+!(a[i]==s[j]));
}
}
return f[la][ls];
}*/
int dis(char a[],char s[])//把s变成a
{
int la=strlen(a+1),ls=strlen(s+1);
for(int i=0;i<=ls;i++) f[i][0]=i;
for(int i=0;i<=la;i++) f[0][i]=i;
for(int i=1;i<=ls;i++)
{
for(int j=1;j<=la;j++)
{
f[i][j]=std::min(std::min(f[i-1][j]+1,f[i][j-1]+1),f[i-1][j-1]+!(s[i]==a[j]));
}
}
return f[ls][la];
}
signed main()
{
std::cin>>n>>m;
for(int i=0;i<n;i++) std::cin>>s[i]+1;//给定的字符串
while(m--)
{
char a[N];
int limit;
std::cin>>a+1>>limit;
int res=0;
for(int i=0;i<n;i++)//枚举有几个字符串可以变成询问的
{
if(dis(a,s[i])<=limit) res++;
}
std::cout<<res<<'\n';
}
return 0;
} 区间DP
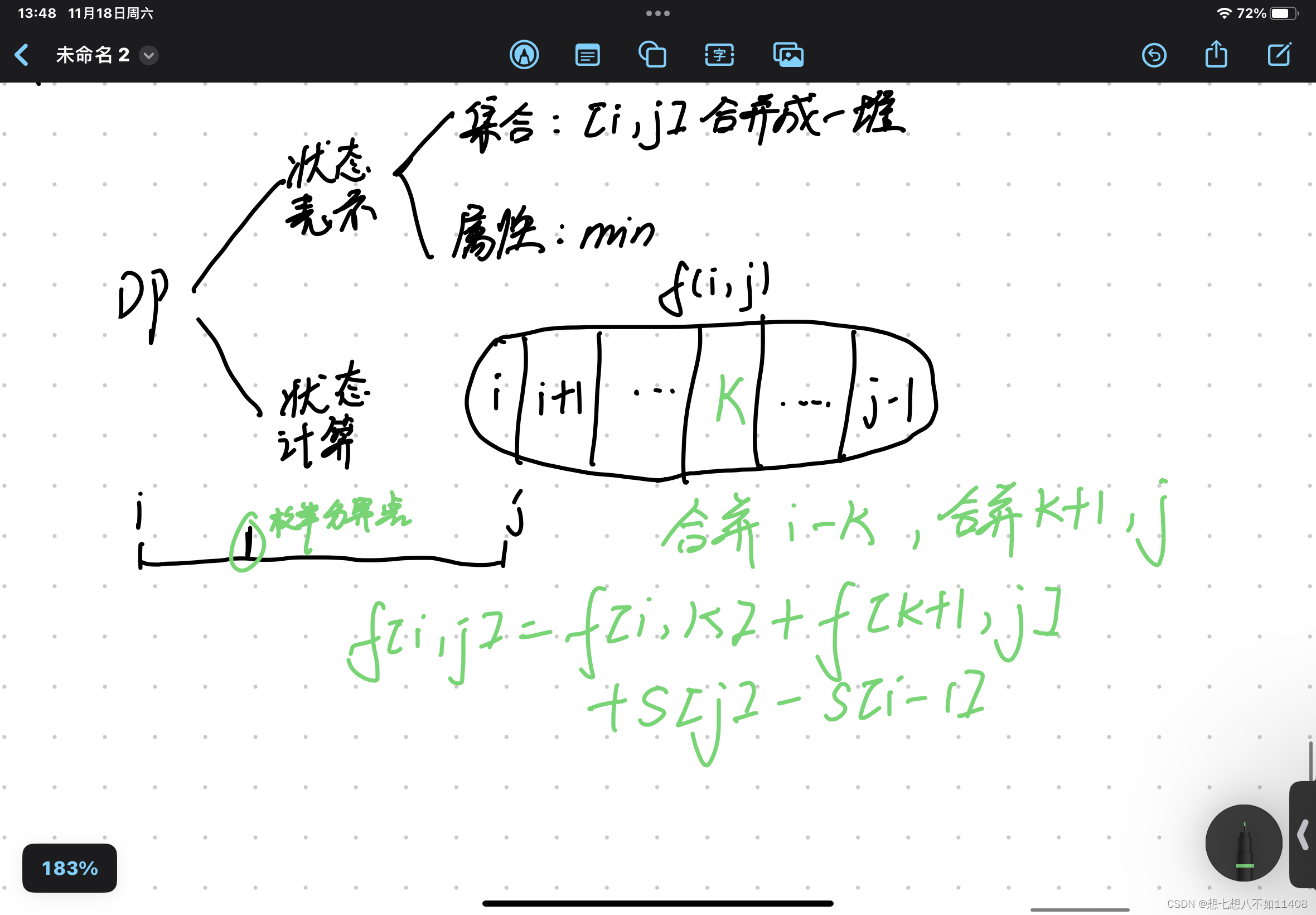
石子合并
282. 石子合并 - AcWing题库
#include<bits/stdc++.h>
const int N=310;
int n;
int a[N],s[N],f[N][N];
signed main()
{
std::cin>>n;
for(int i=1;i<=n;i++)
{
std::cin>>a[i];
s[i]=s[i-1]+a[i];
}
for(int len=2;len<=n;len++)
{
for(int i=1;i+len-1<=n;i++)
{
int j=i+len-1;//右端点
f[i][j]=1e9;
for(int k=i;k<=j;k++)
{
f[i][j]=std::min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1]);
}
}
}
std::cout<<f[1][n];
return 0;
} 
计数类DP
整数划分
900. 整数划分 - AcWing题库
完全背包
朴素版
#include<bits/stdc++.h>
const int N=1e3+10,mod=1e9+7;
int f[N][N];//f[i][j]表示只从1~i中选,且总和等于j的方案数
signed main()
{
int n;
std::cin>>n;
f[0][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=0;j<=n;j++)
{
f[i][j]=f[i-1][j];
if(j>=i) f[i][j]=(f[i-1][j]+f[i][j-i])%mod;
}
}
std::cout<<f[n][n]%mod;
return 0;
} 优化版
#include<bits/stdc++.h>
const int N=1e3+10,mod=1e9+7;
int f[N];//f[i][j]表示只从1~i中选,且总和等于j的方案数
signed main()
{
int n;
std::cin>>n;
f[0]=1;
for(int i=1;i<=n;i++)
{
for(int j=i;j<=n;j++)
{
f[j]=(f[j]+f[j-i])%mod;
}
}
std::cout<<f[n];
return 0;
}数位统计DP
计数问题
338. 计数问题 - AcWing题库

#include<bits/stdc++.h>
int get(std::vector<int> nums,int l,int r)
{
int res=0;
for(int i=r;i>=l;i--)
{
res=res*10+nums[i];
}
return res;
}
int count(int n,int x)//1-n中,x出现次数
{
if(!n) return 0;
std::vector<int> nums;//倒着存数
while(n)
{
nums.push_back(n%10);
n/=10;
}//346,643
n=nums.size();
int res=0;
//如果x为0,x不能出现在首位,故而从n-2开始
for(int i=n-1-!x;i>=0;i--) //枚举x出现在每位的次数
{
if(i<n-1)//如果当前位不是最高位,计算前面的可能个数
{
res+=get(nums,i+1,n-1)*pow(10,i); //get从低位到高位
if(!x) res-=pow(10,i);//如果x为0,前面必须从001开始,因此少一种情况
}
if(nums[i]==x) res+=get(nums,0,i-1)+1; //计算后面的可能
else if(nums[i]>x) res+=pow(10,i);
}
return res;
}
signed main()
{
int a,b;
while(std::cin>>a>>b,a)
{
if(a>b) std::swap(a,b);
for(int i=0;i<10;i++)
{
std::cout<<count(b,i)-count(a-1,i)<<' ';
}
std::cout<<'\n';
}
return 0;
} 状态压缩DP
蒙德里安的梦想
291. 蒙德里安的梦想 - AcWing题库

#include<bits/stdc++.h>
const int N=1<<12;//每一列的状态数
bool st[N];//记录合法的列的状态
#define int long long
std::vector<int> can[N];
int f[12][N];//前i-1列已经填好,且从第i-1列伸到第i列的状态是j
signed main()
{
int n,m;
while(std::cin>>n>>m,n||m)
{
//先预处理出第i-1列的所有合法状态
//先判断是否合法
for(int i=0;i<1<<n;i++)//每一列有n个格子,枚举状态
{
int cnt=0;
bool ok=true;
for(int j=0;j<n;j++)
{
if((i>>j)&1)//当前位填了
{
if(cnt%2)//空格数是奇数
{
ok=false;
break;
}
cnt=0; //归0
}else{
cnt++;
}
}
if(cnt%2) ok=false;
st[i]=ok;
}
memset(can,0,sizeof can);
//预处理出所有第i列前一列的可能状态
for(int i=0;i<1<<n;i++)//枚举这一列的状态
{
for(int j=0;j<1<<n;j++)//前一列的状态
{
if((i&j)==0&&st[i|j]) //没有冲突且空格数为偶数
{
can[i].push_back(j);
}
}
}
memset(f,0,sizeof f);
f[0][0]=1;
for(int i=1;i<=m;i++)//枚举每一列
{
for(int j=0;j<1<<n;j++)//这一列的状态
{
for(auto k:can[j])
{
f[i][j]+=f[i-1][k];
}
}
}
std::cout<<f[m][0]<<'\n';
}
return 0;
} 最短Hamilton路径
91. 最短Hamilton路径 - AcWing题库

#include<bits/stdc++.h>
const int N=1<<20;
int w[25][25],f[N][25];
signed main()
{
int n;
std::cin>>n;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
std::cin>>w[i][j];
}
}
memset(f,0x3f,sizeof f);
f[1][0]=0;
for(int i=0;i<1<<n;i++)
{
for(int j=0;j<n;j++)
{
if((i>>j)&1)
{
for(int k=0;k<n;k++)
{
if((i>>k)&1) f[i][j]=std::min(f[i][j],f[i-(1<<j)][k]+w[k][j]);
}
}
}
}
std::cout<<f[(1<<n)-1][n-1];
return 0;
}树形DP
没有上司的舞会
285. 没有上司的舞会 - AcWing题库
#include<bits/stdc++.h>
const int N=6010;
int f[N][2],happy[N];
bool hasfa[N];
int h[N],ne[N],e[N],idx;
void add(int a,int b)
{
e[idx]=a,ne[idx]=h[b],h[b]=idx++;
}
void dfs(int u)
{
f[u][1]=happy[u];
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
dfs(j);
f[u][1]+=f[j][0];
f[u][0]+=std::max(f[j][0],f[j][1]);
}
}
signed main()
{
int n;
std::cin>>n;
for(int i=1;i<=n;i++) std::cin>>happy[i];
memset(h,-1,sizeof h);
for(int i=1;i<n;i++)
{
int a,b;//b是上司
std::cin>>a>>b;
add(a,b);
hasfa[a]=true;
}
int root=1;
while(hasfa[root]) root++;
dfs(root);
std::cout<<std::max(f[root][0],f[root][1]);
return 0;
}记忆化搜索
滑雪
901. 滑雪 - AcWing题库
#include<bits/stdc++.h>
const int N=310;
int h[N][N],mem[N][N];
int dx[]={0,1,0,-1},dy[]={1,0,-1,0};
int n,m;
int dfs(int x,int y)
{
int &u=mem[x][y];
if(u!=-1) return mem[x][y];
u=1;//至少可以走当前点
for(int i=0;i<4;i++)
{
int a=x+dx[i],b=y+dy[i];
if(a>=1&&b>=1&&a<=n&&b<=m&&h[a][b]<h[x][y])
u=std::max(u,dfs(a,b)+1);
}
return u;
}
signed main()
{
std::cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++) std::cin>>h[i][j];
}
memset(mem,-1,sizeof mem);
int res=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
res=std::max(res,dfs(i,j));
}
}
std::cout<<res;
return 0;
}完结,撒花~