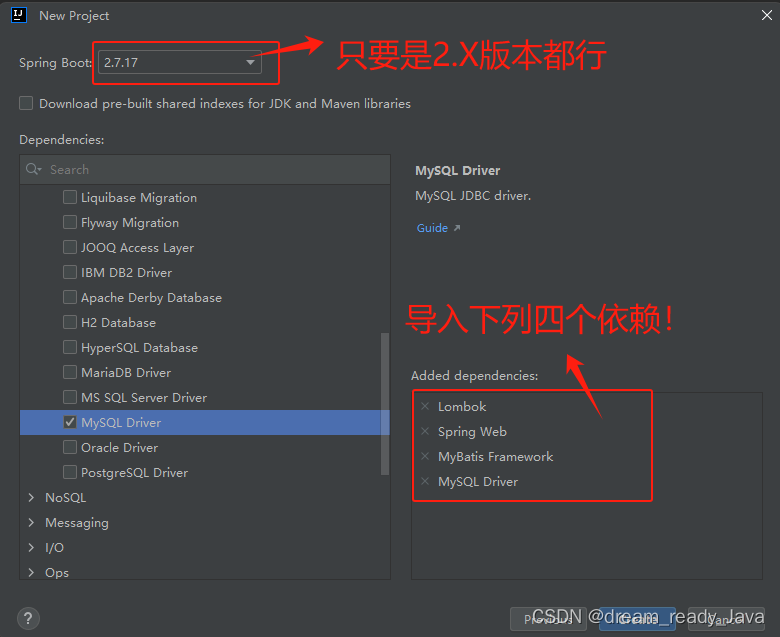
美团2024届秋招笔试第一场编程真题

先提一个小知识：题目中凡是提到树结构都要使用图的存储方式，只有二叉树例外。

分析：在树结构中，孩子和父节点是相邻节点，而父节点可能有多个孩子节点。在染色的过程中，本质是父子节点满足条件就染成红色。具体染色策略以下图为例

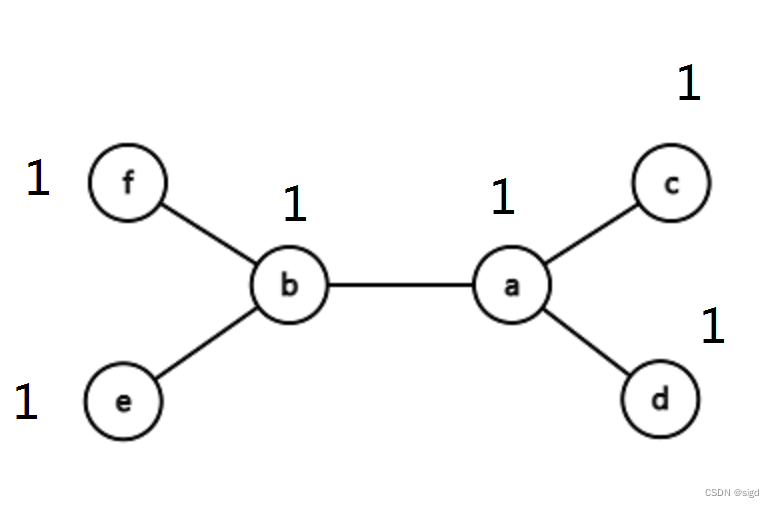
图中节点权值均为1，也就是任意相邻节点都可以满足染色条件，显然我们不能先将a和b染色，那样就只有2个点能被染色，而是应该先染色<f,b>或 <e,b>，然后再<a,c> 或<a,d>，这样可以染4个点。下图又该先考虑染色那些节点呢？

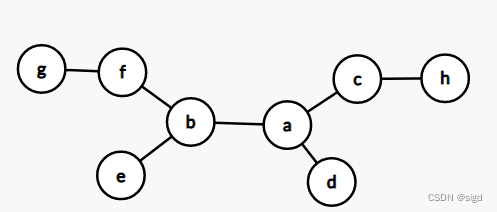
这样总结出贪心策略：先处理叶子结点的染色，然后处理内部节点。比如上图，先处理<g,f>。如果能染色，哪么将g,f标记红色，同时<f,b>就不可能染色了如果不能染色，未来还可以继续试探<f,b>。

实现方法：先处理最外层节点（叶子），外层处理完了，这些叶子就可以不要了，往内层推进。

使用拓扑排序的思想。当然不是入度0节点入队，这可不是有向图。而是度为1（叶子）节点入队，从树叶向树根进行拓扑处理。

图问题的复杂度正常都是遍历所有的结点，也就是访问所有的点和边，此图n-1条边，复杂度为O(n)。

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
ll n,a[100005],d[100005],red[100005],v[100005],ans=0;
vector <int> e[100005];
bool isP(ll x)/**< 平方数判定 */
{
    ll y=(int)sqrt(x);
    return y*y==x;
}
int main()
{
    ios::sync_with_stdio(0),cin.tie(0);
    int i,j,x,y;
    cin>>n;
    for(i=1;i<=n;i++)
        cin>>a[i];
    for(i=1;i<n;i++)
    {
        cin>>x>>y;
        e[x].push_back(y),e[y].push_back(x);
        d[x]++,d[y]++;/**< d数组统计度 */
    }
    queue<int>q;
    for(i=1;i<=n;i++)
        if(d[i]==1)/**< 度为1的入队*/
        q.push(i);
    while(q.size())/**< 模拟拓扑排序处理方法 */
    {
        x=q.front();
        v[x]=1;/**< 标记这个节点，避免重新被入队处理 */
        q.pop();
        for(i=0;i<e[x].size();i++)/**< 找到x所有邻接点 */
        {
            y=e[x][i];
            if(v[y]) /**< y已经访问过，其实y一定是x的子节点 */
                continue;
            if(red[x]==0&&red[y]==0&&isP(a[x]*a[y]))/**< x和它父节点y满足条件 */
                red[x]=red[y]=1,ans+=2;/**< 标记颜色，计数器+2 */
            d[y]--;
            if(d[y]==1)/**< 度为1说明y子节点都处理完了，此时可以入队 */
              q.push(y);
        }
    }
    cout<<ans;
    return 0;
}