引言
GAN的风暴席卷了整个深度学习圈子,任何任务似乎套上GAN的壳子,立马就变得高大上了起来。那么,GAN究竟是什么呢?
GAN的主要应用目标:
生成式任务(生成、重建、超分辨率、风格迁移、补全、上采样等)
GAN的核心思想:生成器G和判别器D的一代代博弈
生成器:生成网络,通过输入生成图像
判别器:二分类网络,将生成器生成图像作为负样本,真实图像作为正样本
learn 判别器D:
给定G,通过G生成图像产生负样本,并结合真实图像作为正样本来训练D
learn 生成器G:
给定D,以使得D对G生成图像的评分尽可能接近正样本作为目标来训练G
G和D的训练过程交替进行,这个对抗的过程使得G生成的图像越来越逼真,D“打假”的能力也越来越强。
觉得不是很好理解嘛?别着急,慢慢往下看!
1 从极大似然估计说起
补充:
分布的表示:P(x)
表示该分布中采样到样本x的概率,试想如果我们知道该分布中每个样本的采样概率,那么这个分布也就可以以这种形式表示出来了。
确定分布的表示:P(x;𝜃)
其中𝜃表示该分布的参数,该分布的具体形式确定了(比如 P(x;𝜃) 可以是高斯分布,𝜃就是高斯分布的均值 µ和方差𝜌
先来介绍一下极大似然估计:
1.1 极大似然估计要解决的问题
-
给定一个数据分布
-
给定一个由参数𝜃定义的数据分布
-
我们希望求得参数𝜃使得
尽可能接近
可以理解成:
是某一具体的分布(比如简单的高斯分布),而
是未知的(或者及其复杂,我们很难找到一个方式表示它),我们希望通过极大似然估计的方法来确定𝜃 ,让 能够大体表达
。
1.2 极大似然估计的解决方案
-
从
采样m个样本
-
计算采样样本的似然函数
-
计算使得似然函数 L 最大的参数𝜃 :
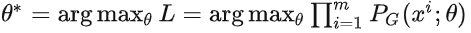
这里再啰嗦一下极大似然估计为什么要这么做:
可以理解成是非常复杂的分布,不可能用某个数学表达精确表示,因此我们只能通过抽象,使用一个具体的分布模型
近似
所以,求 的参数 𝜃的策略就变成了:
我们认为来自 的样本
在
分布中出现的概率越高,也就是
越大,
和
就越接近。
因此,我们期待的𝜃就是使得 最大的𝜃.
即:
![]()
咱们继续推导:
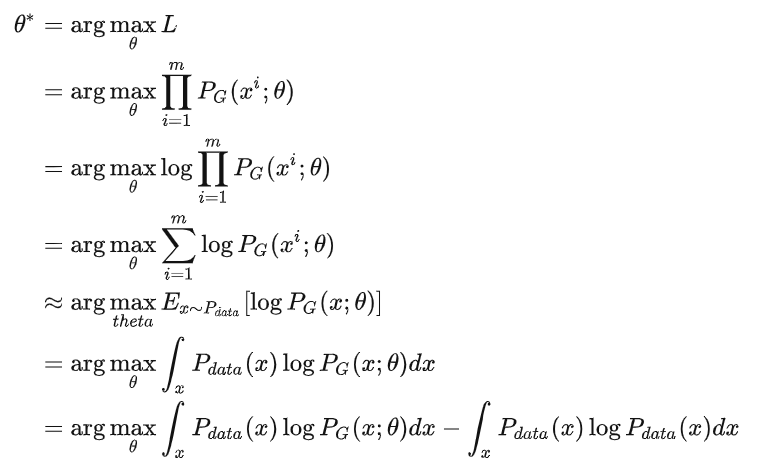
关于最后一步:
因为我们求取的是𝜃 ,而式一 与𝜃无关,因此加上这一项并不影响等式。
加上这一项是为了后面的推导,把极大似然函数的式子化简成KL散度的表达式
(公式推导接上)
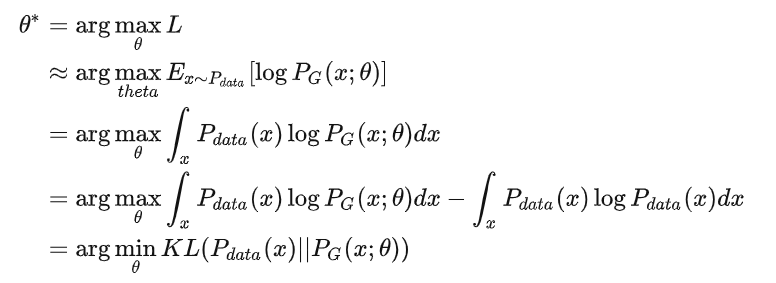
KL散度:
KL(P||Q) 衡量P,Q这两个概率分布差异的方式:
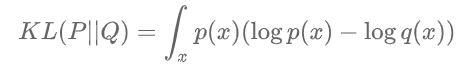
1.3 极大似然估计的本质
找到𝜃 使得 与目标分布
的KL散度尽可能低,也就是使得两者的分布尽可能接近,实现用确定的分布
极大似然
2 GAN的基本思想
2.1 生成器:有问题?试试神经网络!
GAN的主要应用是集中在生成
本质就是在做一个极大似然估计的事情,我们希望可以用某一种具体的分布形式 尽可能逼真地表达分布
,这样我们就相当于是得到了
,并据此分布
采样(也就是做生成式的任务):
-
确定具体分布的形式
-
极大似然估计求得𝜃.我们认为我们可以使用
近似表达
-
基于
采样做生成
那么最直接的想法: 直接用高斯分布模型,但是高斯分布的capacity太弱了,不能很有效地推广至去拟合各种差异很大地目标图像分布
想要得到更general的 ,为什么不考虑使用具有强大拟合能力的神经网络来做呢???!!!
我们不妨设计一个神经网络G来得到更general的 ,大概的结构图如下:
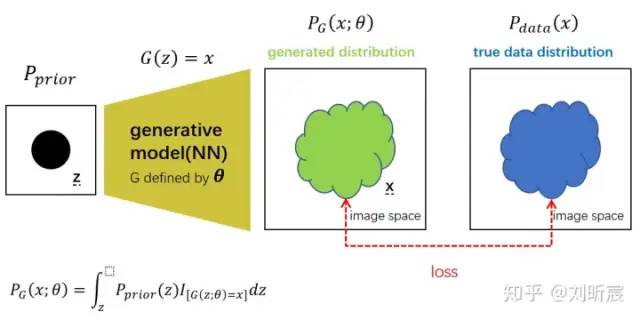
解释一下:
整体pipeline:
-
我们先选取一个简单的先验分布
,并从该先验分布中采样z作为输入,输入到神经网络G,得 G(z)=
生成图像
.我们通过这种方式构建了生成分布
。此时该分布主要由神经网络G决定,参数𝜃由网络参数定义.我们可以通过输入z来在该分布上采样
.
-
我们的目标是
,我们希望我们构建的
与它尽可能接近。我们无法获得
的具体表达形式,我们只能获得它的样本。
-
类似极大似然估计,我们通过比较两个分布样本的差异设计loss来调节优化神经网络G的参数𝜃,从而实现将分布
向
拉近,从而达到用
拟合表达
的效果。
表示一个先验分布,我们生成图像
需要输入的code z 就是服从这个先验分布的。这个先验分布比如可以是:高斯分布
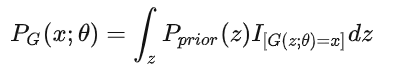
指示函数 表示当 [] 内的条件为真时取值为1,为假时取值为0
也就是说分布 采样
的概率是所有能够使得
成立的z出现的概率之和,而z在这里是符合先验分布
的。
显然, 的计算是非常困难的。
然而, 的计算又是非常必要的,因为我们需要验证
在不断靠近
.
现在这种情况使用极大似然估计根本无从下手啊!!!
那么现在,GAN来了!!!
2.2 判别器:有问题?GAN来了!
GAN由生成器G和判别器D组成。
其实上面我们已经基本介绍了生成器G的由来了,并且我们遇到了一个问题: 极其复杂的计算方式导致使用极大似然估计根本无从下手啊!!!
为了解决这个问题,我们引入了判别器D!
现在GAN的结构就完备了!!
对于生成器G:
-
G 是一个函数,输入
~
,输出(上面已经介绍了)
~
-
先验分布
,
和G共同决定的分布
对于判别器D:
-
D是一个函数,输入
~
,输出一个scalar
-
D用于评估
和
之间的差异(解决上一小节提出的问题)
那么,GAN的最终目标-->用符号化语言表示就是:
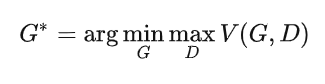
我们的目标是得到使得式子 最小的生成器
.
关于V:
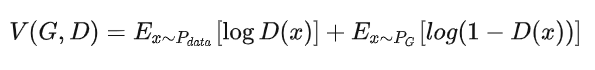
给定G, 衡量的就是分布
和
的差异。
因此, 也就是我们需要的使得差异最小的 G .
详细解释 V(G,D) :
对于 :
固定G ,最优 最大化:
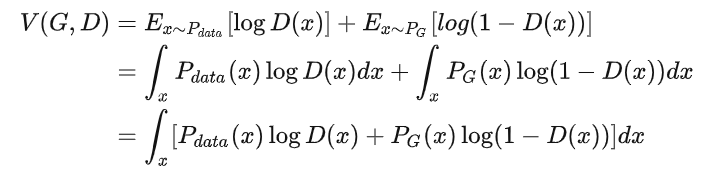
假设D(x) 可以表达任何函数
此时再固定 x ,则对于 ,我们可将其看成是关于D的函数:
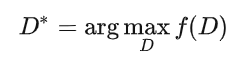
解得
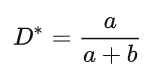
即:
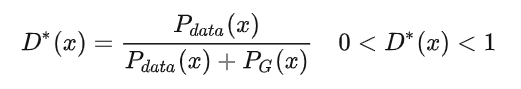
则此时对于原式 V(G,D) (将 代入):
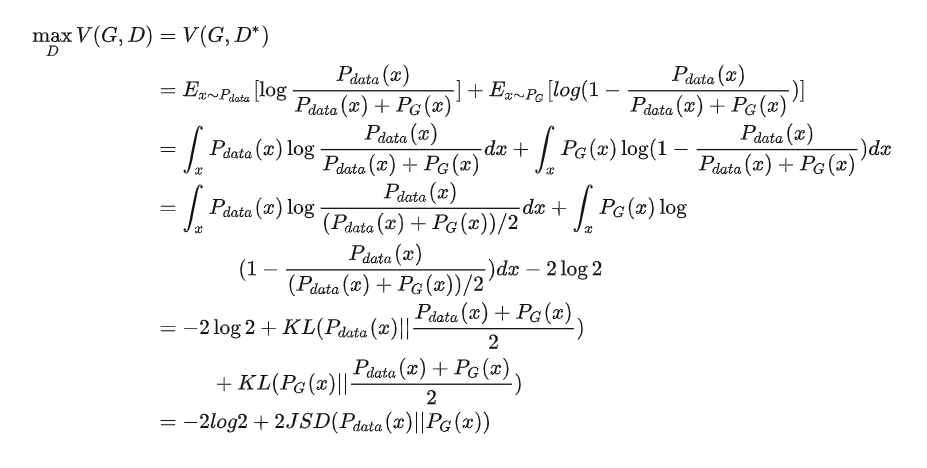
JSD表示JS散度,它是KL散度的一种变形,也表示两个分布之间的差异:
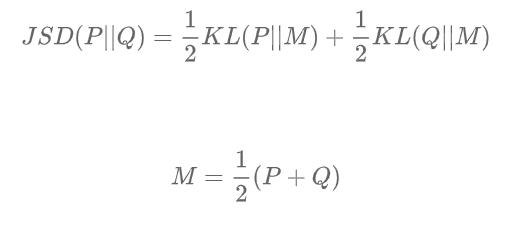
与KL散度不同,JS散度是对称的。
以上的公式推导,证明了 确实是衡量了
和
之间的差异。
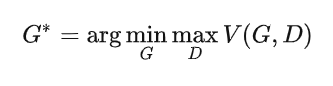
此时,最优的G:
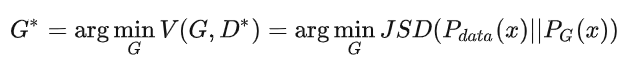
也就是使得 最小的G
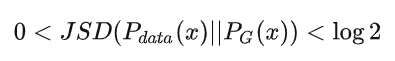
当 时,表示两个分布完全相同。
对于 ,令
我们该如何优化从而获得 呢???
我们希望通过最小化损失函数L(G) ,找到最优的G。
这一步可以通过梯度下降实现:
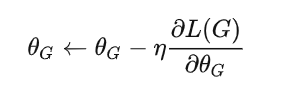
具体算法参考:
第一代:
-
给定
(随机初始化)
-
确定
使得
最大。此时
, 表示
和
的JS散度
-
梯度下降:
.得到
第二代:
2. 给定
-
确定
使得
最大。此时
, 表示
和
的JS散度
-
梯度下降:
.得到
。。。
后面的依此类推
以上算法有一个问题:如何确定 使得 V(D,G) 最大???
也就是:给定 G,如何计算
回答:
从 采样
从 采样
因此我们可以将 从期望值计算改写为对样本计算(近似估计):
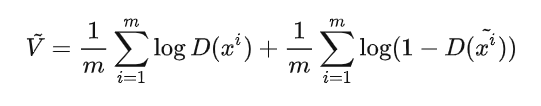
这很自然地让我们想到二分类问题中常使用的交叉熵loss
因此,我们不妨联想:
D是一个二分类器,参数是 来自
的采样
作为正样本
来自 的采样
作为负样本
那么此时,我们就将问题转化成了一个二分类问题:
交叉熵loss大 --> 和
JS散度小
交叉熵loss小 --> 和
JS散度大
此时,D就是可以使用一个神经网络作为二分类器,那么确定D,也就是可以使用梯度下降来优化获得D的最终参数。
GAN的最终算法流程:
初始化参数 (for D)和
(for G)
对于训练的每一轮:
第一部分 学习优化判别器D:
-
从
采样
-
从
采样
-
通过生成器
获得生成样本
-
梯度下降更新
来最大化 :
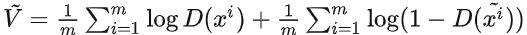
:
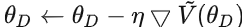
注:以上第一部分可以重复多次:此过程本质上是在测量两分布之间的JS散度
第二部分 学习优化生成器G:
-
再从
采样另一组
-
梯度下降更新
来最小化 :
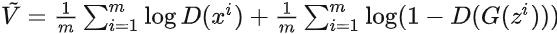
:
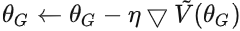
.实际上
第一项与G无关,梯度下降只需最小化
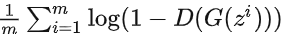
即可。
注:以上过程仅一次
最后的话:
其实在GAN之前,就已经有Auto-Encoder,VAE这样的方法来使用神经网络做生成式任务了。
GAN的最大的创新就是在于非常精妙地引入了判别器,从样本的维度解决了衡量两个分布差异的问题。
这种生成器和判别器对抗学习的模式,也必将在各种生成式任务中发挥其巨大的威力。