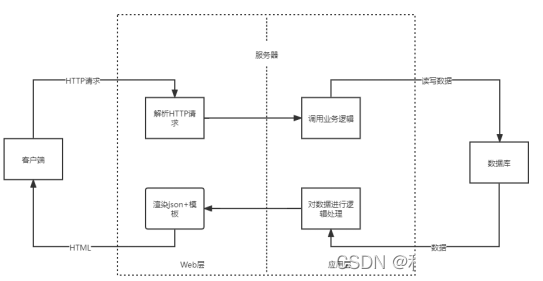
一、神经网络的一个重要性质

1.1 重要性质

自动从数据中学习到合适的权重参数

1.2 称呼

共n层神经元，称之为n-1层网络

• 输入层
• 中间层（隐藏层）
• 输出层

1.3计算神经网络

节点值*权重值+偏置值=输出值

根据输出值的大小计算出节点值

• 输出值超过0，节点值是1
• 输出值小于等于0，节点值是0

将原来的表达式用新函数$$h(x)$$来表示

二、激活函数登场

简介

将输入信号的总和转换为输出信号

• 输入：输入信号的加权总和
• 激活函数：h（a）
• 计算得到结果

可以在神经元内部中明确的显示出激活函数的激活过程

激活函数是连接感知机和神经网络的桥梁

三、感知机使用的激活函数

3.1 使用小技巧将numpy数组的值进行转化

使用小技巧将numpy中数组类型的值进行转化

import numpy as np
x= np.array([-1.0,1.0,2.0])
x
Out[4]: array([-1.,  1.,  2.])
y=x>0
y
Out[6]: array([False,  True,  True])
y=y.astype(np.int)
yy
Traceback (most recent call last):
  File "D:\ANACONDA\envs\pytorch\lib\site-packages\IPython\core\interactiveshell.py", line 3343, in run_code
    exec(code_obj, self.user_global_ns, self.user_ns)
  File "<ipython-input-8-6daa41ef554c>", line 1, in <module>
    yy
NameError: name 'yy' is not defined
y
Out[9]: array([0, 1, 1])

通过一个小技巧来将数组中的不同元素转换成为输入值0或者1

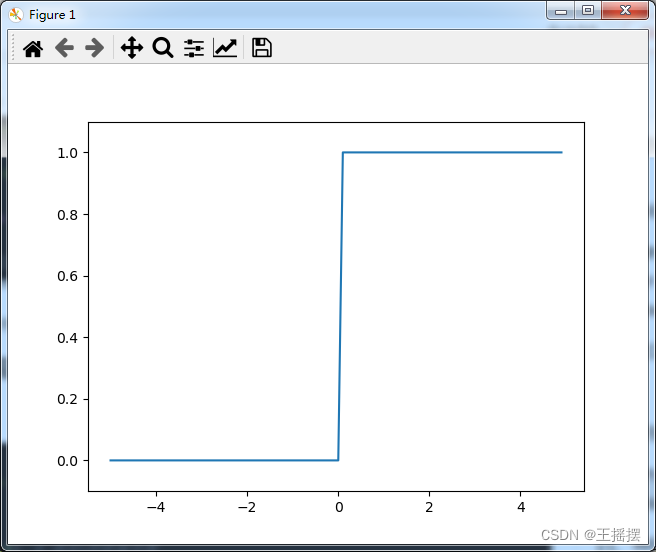
3.2 阶跃函数的实现：一旦超过阈值就发生变化

是会跳跃变化的函数

def step_function(x):
    return np.array(x > 0, dtype=np.int)


x = np.arange(-5, 5, 0.1)  # 指定x的取值范围
y = step_function(x)
plt.plot(x, y) # 给定输入的x和y
plt.ylim(-0.1, 1.1) # 指定y轴的范围
plt.show()

四、神经网络使用的激活函数

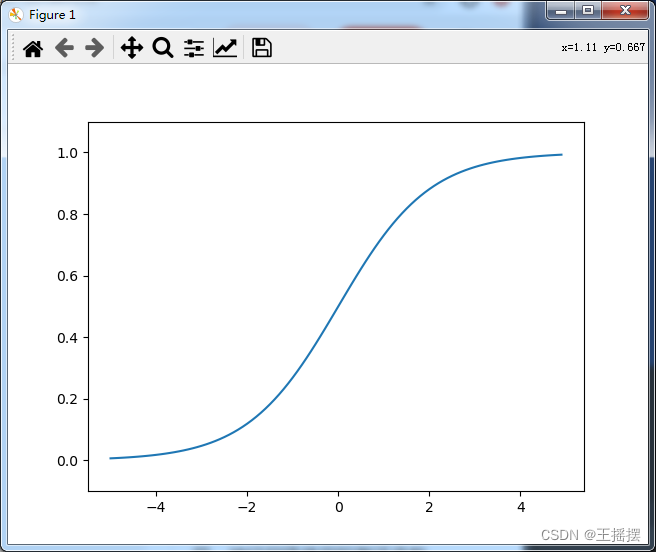
4.1 sigmod函数的实现

函数能支持数组运算很重要的一个功能就是numpy数组支持广播的功能

可以让数组和标量在根据实际情况在需要的时候使用

import numpy as np
import matplotlib.pylab as plt


def sigmod(x):
    return 1 / (1 + np.exp(-x))


x = np.arange(-5, 5, 0.1)  # 指定x的取值范围
y = sigmod(x)
plt.plot(x, y)  # 给定输入的x和y
plt.ylim(-0.1, 1.1)  # 指定y轴的范围
plt.show()

4.2 两种不同的激活函数的比较

1. 二者的平滑性不同
2. sigmod 函数的平滑性对于神经网络的学习具有重要的意义
3. 阶跃函数只能返回0或者1

感知机中的神经元的阶跃函数返回的是二元信号
神经网络中的神经元sigmod函数返回的是 实数值信号

不管输入的信号值是多少，输出的值均在0和1之间

二者都是非线性函数

4.3 神经网络中的使用

在神经网络中必须使用非线性函数

• 线性函数的使用对于神经网络的层数是没有意义的

激活函数必须使用非线性函数

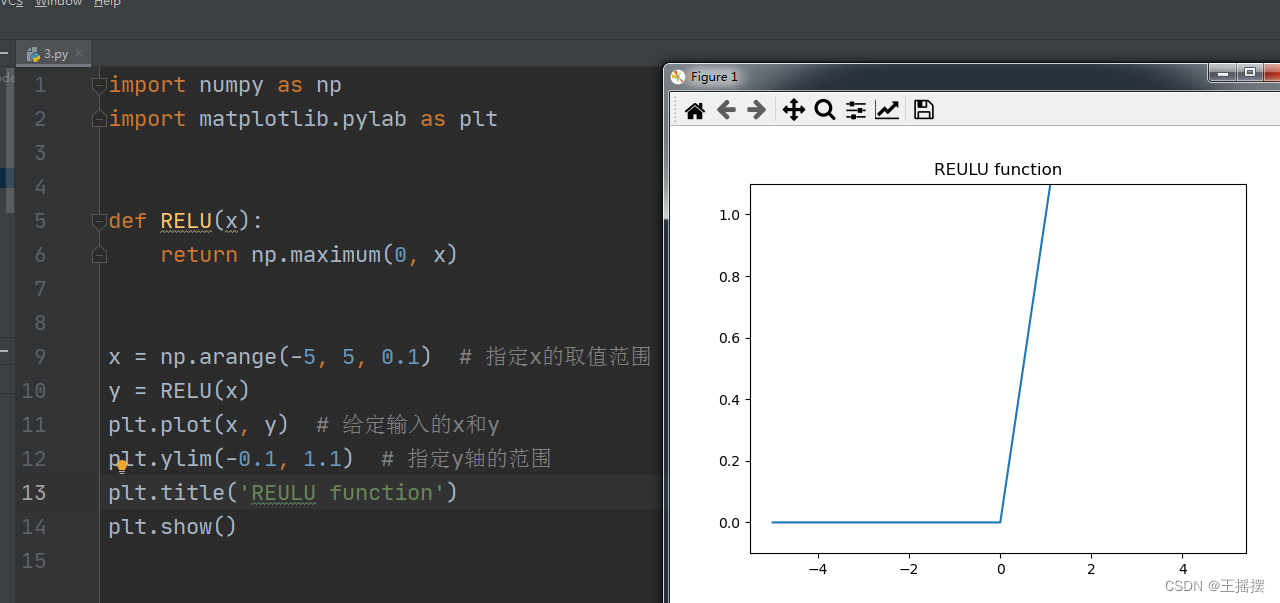
五、新兴的RELU函数

5.1 介绍

• 函数输入大于0时，直接输出该值
• 否则输出0

5.2 实现