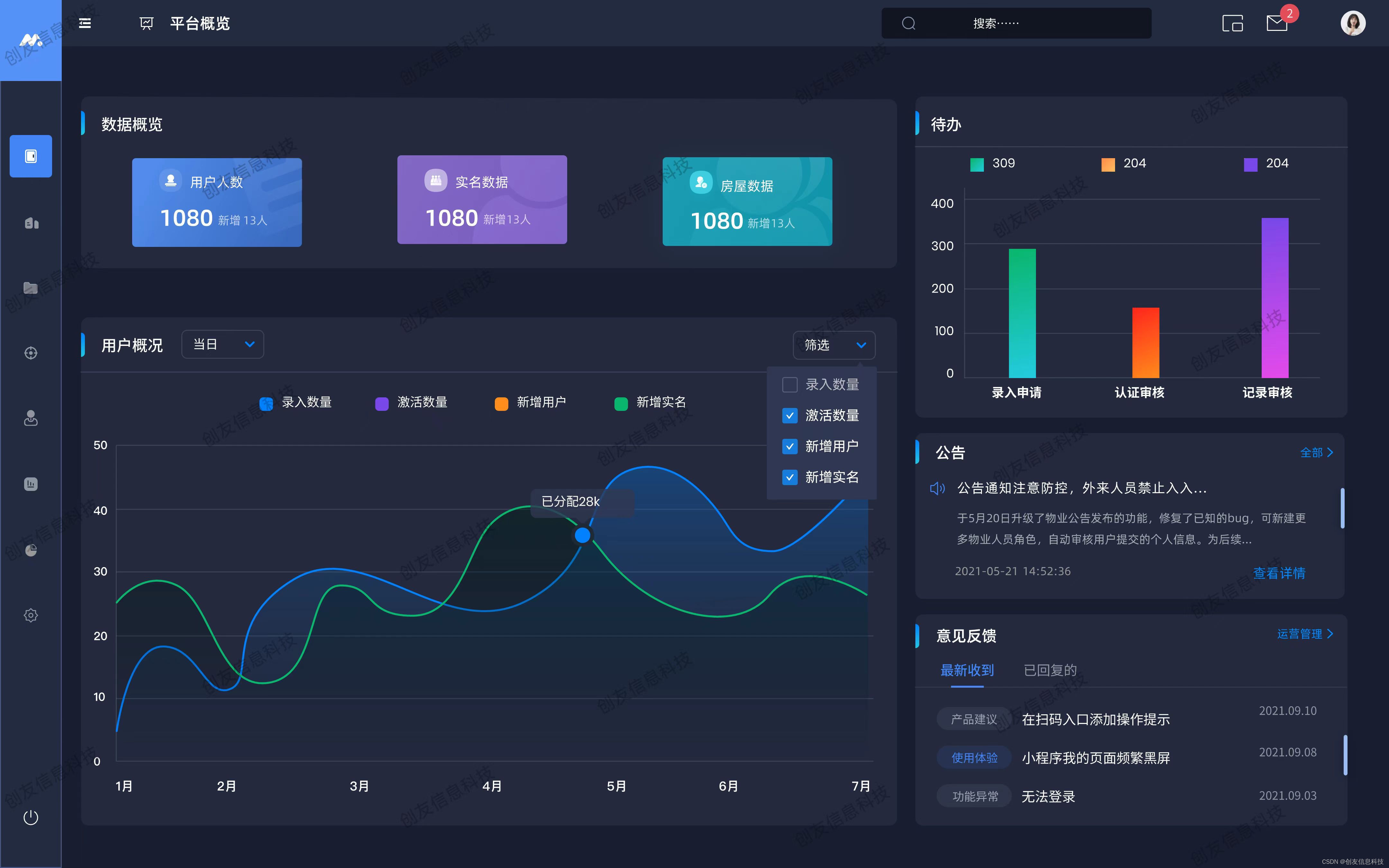
最大功率传输

当工程师设计电子电路时，他们会跟踪许多不同的参数，但最重要的参数之一是功率。 在现代电路中，功率在多个阶段中不断变化，有时由于耗散元件造成的损耗很大，需要使用放大器来增加功率。

通常优选最大化电路每一级之间的功率传输，以便尽可能避免任何再放大。 例如，电信领域中的信息传输就是这种情况。

在本文中，我们重点关注一个简单但重要的概念，称为最大功率传输定理 (Maximum Power Transfer Theorem，MPTT)，它解释了功率如何最有效地从源传输到接收器。

为了介绍这个概念，我们首先对戴维南电路进行简单的观察，以了解传输的功率取决于电阻值。 我们还强调传输功率的优化和电路效率之间需要进行的区分。

在第二部分中，我们解释一般情况下的 MPTT 并通过提供演示来证明它。

最后，我们重点关注与该定理相关的阻抗匹配概念，它是用于优化功率传输的重要技术。

1、概述

假设一个线性电路，该电路可以简化为给定的戴维南等效模型 $V_{Th}$、$R_{Th}$，其端子连接到可变负载 $Z$，如下图 1 所示：

图1：提供可变负载 Z 的电路的戴维宁模型

如图所示，我们将考虑 $V_{Th}$ 和 $R_{Th}$ 的具体值。 根据欧姆定律，流入电路的公共电流可以写成：$I=V_{Th}/(R_{Th}+Z)$。

由于传输到负载的功率可以表示为 $P_Z=Z\times I^2$，因此我们可以将 $P_Z$ 写成 Z 和已知电路参数的函数： $P_Z=(Z\times V_{Th}^2)/(R_{Th}+Z{)}^2$。

下面的图2显示了图形 $P_Z=f(X)$，其中 $X=Z/R_{Th}$，通过 MatLab® 等数据软件绘制的：

图2：P_Z=f(Z/RTh)

正如该图中突出显示的那样，$Z=R_{Th}$ 时似乎达到了最大传输功率。 然而，这个峰值并不是很窄，因为对于比率 $X=2$，传输的功率仍然是最大值的 90%。

值得注意的是，当 $X=1$ 时，无法达到由比率 $\eta =P_Z/P_S$ 定义的最大效率（其中 PS 是源产生的功率），而 $X=1$ 是最大传输功率的唯一条件。 这种区别令人困惑，并且在我们之前的一篇文章中已经非常详细：放大器的输入和输出阻抗。

我们可以注意到，当达到最大传输功率时，效率仅为 50%。 这个数字可以很容易地解释为，当 $R_{Th}=Z$ 时，内部源电阻 ($R_{Th}$) 的耗散功率与负载 $Z$ 中的耗散功率相同。当满足不等式$ Z>>R_{Th}$ 时，即可达到最大效率， 在这种情况下，内部源电阻不会消耗功率。

2、最大功率传输定理 (MPTT)

在本节中，我们介绍 MPTT 的一般形式，并提出一个演示。

我们建议如下图3作为说明参考：

图3：为负载（ZL）供电的电源（VS、ZS）

该电路可以被视为戴维宁模型，其中 $V_S=V_{Th}$和$R_S=R_{Th}$ 作为源和负载之间电路的等效电阻，也可以被视为非理想源，其内部阻抗 $Z_S=R_S+j{X}_S$ 提供复杂负载 $Z_L=R_L+j{X}_L$。

MPTT 规定，为了最大限度地提高传输到负载的功率，需要阻抗匹配。 为此必须满足两个条件：

• 电抗必须补偿，即$X_S=-X_L$
• 电阻必须匹配，即$R_S=R_L$

由于$R_e(Z_S)=R_e(Z_L)$ 和$I_m(Z_S)=-I_m(Z_L)$，我们可以说 $Z_S$ 和 $Z_L$ 是共轭的（有关更多信息，请参阅我们有关复数的教程）。 在此条件下，负载 $R_L$ 中传递的功率最大并且满足公式 1：

等式1：最大传输功率值

3、示例

该定理的演示包括表达负载中的功率并通过求导运算找到其最大值。

我们首先写出电路中电流的模：$|I|=|V|/(|Z_S|+|Z_L|)$。 传输到负载的功率可以用$|I|$的RMS值来表示，其平方值为$I_{RMS}^2=|I{|}^2/2$。

负载中的功率满足，因此：

为了最大化这个分数，我们将最小化分母。 通过选择 $X_S=-X_L$ 可以轻松最小化甚至补偿电抗项。

幂的表达式可以简化为：

为了再次最小化分母$D$，我们进行等于零的推导：$dD/d{R}_L=0$。 这个推导导致$-R_S^2/R_L^2+1=0\Rightarrow R_S=R_L$。

然而，当导数等于 0 时，要么达到最大值，要么达到最小值。 为了确保 $R_S=R_L$ 最小，我们计算二阶导数 $d^{2}D/d_{RL}^2=2(R_S^2/R_L^3)$。

对于正值 $R_S$ 和 $R_L$，二阶导数为正，这意味着分母是凸函数（与函数 $x^2$ 形状相同）。 然后我们可以确认$R_S=R_L$ 达到最小值。

综上所述，当$R_S=R_L$且$X_S=-X_L$时，负载中的功率最大。 当满足这些条件时，我们可以确认满足等式1。

4、阻抗匹配

我们在上一节中简要提到了术语阻抗匹配，这里我们解释一下这个概念的重要性，特别是在电信领域。

阻抗匹配技术用于优化功率传输而不是效率。

阻抗匹配技术广泛用于优化传输线中的信号传输。 传输线是一种特殊的双线，适合以最小的损耗传导高频信号。

它们通常用等效电路表示，如下图 4 所示：

图4：连接到负载的接线的示例

我们需要注意的是，图 4 中所示的组件并不真正存在于传输线中，这种表示形式的存在是为了反映传输线的电气行为。

线路的线性电阻和电感用 $R$ 和 $L$ 表示。两个导体之间的材料特性用电导 $G$ 和电容器 $C$ 表示。连接在传输线端子上的负载 $Z$ 可以表示 电视、扩音器、电话……等

我们定义特性阻抗为$Z_C=\sqrt{L/C}$，它代表传输线的阻抗。 与欧姆定律类似，这个特定的阻抗简单地表示传输线上传播的电压和电流的比率。 例如，同轴电缆是 $Z_C=50\Omega$ 的传输线。

特性阻抗的表达式来自著名的电报员方程，而该方程本身又来自电磁学的麦克斯韦方程组。

在此示例中，确保功率以最佳方式从电源传输到负载非常重要。 将负载 Z 与线路的特性阻抗相匹配确实可以避免信号反射回源，从而导致干扰。 例如，在电话线路中，阻抗匹配不良会产生回声。

5、总结

• 对于某些电路，需要最大传输功率，特别是在电信领域。 我们在本文中提出了最大功率传输定理 (MPTT)，该定理解释了在什么要求下满足此条件。
• 在第一部分中，我们从戴维南电路观察到，当电路中存在的两个电阻相等时，达到最大传输功率。 我们还解释说，重要的是不要将最大传输功率与电路效率混淆，尽管它们的定义相似。
• 在第二部分中，我们通过解释实现最大功率传输需要两个条件来详细介绍 MPTT。 不仅电阻必须相等，电抗也必须相互补偿。 此外，还提供了该定理的演示，可以帮助读者理解该定理与效率概念之间的区别。
• 最后，一小节详细介绍了电信领域阻抗匹配的概念。