记录一下算法题的学习6
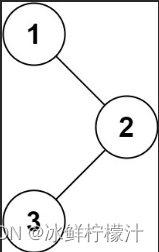
首先我们要回忆一下怎么样遍历一个树:
三种遍历概念
- 先序遍历:先访问根节点,再访问左子树,最后访问右子树。
- 后序遍历:先左子树,再右子树,最后根节点。
- 中序遍历:先左子树,再根节点,最后右子树。
- 每一个子树遍历时依然按照此时的遍历顺序。
leetCode算法简单题目:
题目:给定一个二叉树的根节点 root ,返回 它的 中序 遍历
代码与思路分析:
真香递归代码展示:
/**
*二叉树的中序遍历 先左子树,再根节点,最后右子树。
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> tree = new ArrayList<Integer>();
inorder(root, tree);
return tree;
}
public void inorder(TreeNode root, List<Integer> tree) {
if (root == null) {
return;
}
//中序遍历 定义 inorder(root) 表示当前遍历到 root\textit{root}root 节点
//inorder(root.left) 来遍历 root 节点的左子树
inorder(root.left, tree);
//然后将root 节点的值加入答案
tree.add(root.val);
//inorder(root.right) 来遍历 root 节点的右子树
inorder(root.right, tree);
}
}
栈与迭代代码展示:
这里我们要了解栈的特点:先进后出,后进先出
- 先序遍历,出栈顺序:根左右; 入栈顺序:右左根
- 中序遍历,出栈顺序:左根右; 入栈顺序:右根左
- 后序遍历,出栈顺序:左右根; 入栈顺序:根右左
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> tree = new ArrayList<Integer>(); //定义一个遍历后的二叉树列表
Deque<TreeNode> stack = new LinkedList<TreeNode>();//定义栈
//root为空并且stack为空,遍历就会结束
while (root != null || !stack.isEmpty()) {
// 满足上面条件 ,先根后左入栈
while (root != null) {
stack.addFirst(root); //addFirst(e)等价于 push(e),
root = root.left;
}
//这里仔细分析
// 如果这里root==null,说明上一步的root没有左子树
// 1. 执行左出栈。因为此时root==null,导致root.right一定为null(左子树里的右,可能有点混,仔细想想)
// 2. 执行下一次外层while代码块,根出栈。此时root.right可能存在(这里是根节点的右子树)
// 3a. 若root.right存在,右入栈,再出栈
// 3b. 若root.right不存在,重复步骤2执行下一次外层while代码块,即root为空并且stack为空,遍历就会结束
root = stack.removeFirst(); //1.removeFirst()等价于pop()
tree.add(root.val);//左子树遍历完,直接将根节点添加上去
root = root.right; //然后右子树
}
return tree;
}
}这里我事先并不知道Deque是什么,查了一下资料,在这里简单做个记录:
Deque是一个双端队列接口,继承自Queue接口,Deque的实现类是LinkedList、ArrayDeque、LinkedBlockingDeque,其中LinkedList是最常用的。
它有三种用途:a.普通队列(一端进一端出),b.双端队列(两端都可以进出),
c.堆栈Deque deque = new LinkedList()
我们在这里使用的就是堆栈,Deque堆栈操作方法:push()、pop()、peek()。下面代码会用到。
双端队列用作 LIFO(后进先出)堆栈。应优先使用此Deque接口而不是遗留 Stack 类。在将双端队列用作堆栈时,元素被推入双端队列的开头并从双端队列开头弹出。
堆栈方法完全等效于Deque 方法
| 堆栈方法 | 等效Deque方法 |
| push(e) | addFirst(e) |
| pop() | removeFirst() |
| peek() | peekFirst() |
这里展示二叉树的前序遍历:
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> tree = new ArrayList<Integer>();
Deque<TreeNode> stack = new LinkedList<TreeNode>();
if (root == null) {
return tree;
}
while (!stack.isEmpty() || root != null) {
while (root != null) {
tree.add(root.val);
stack.addFirst(root);
root = root.left;
}
root = stack.removeFirst();
root = root.right;
}
return tree;
}
}这里展示二叉树的后序遍历(提示:这是我看到的leedcode中对官方代码最清晰的解释):
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> tree = new ArrayList<Integer>();
Deque<TreeNode> stack = new LinkedList<TreeNode>();
if (root == null) {
return tree;
}
//在后序遍历中,我们使用一个prev来记录历史访问记录
//回溯到父节点时,可以由此来判断,上一个访问的节点是否为右子树
TreeNode prev = null;
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
//从栈中弹出左子树‘先进后出’ 左子树访问完毕
root = stack.pop();
//现在要确定的是是否有右子树,或者右子树是否访问过
//如果没有右子树,或者右子树访问完了,也就是上一个访问的节点是右子节点时
//说明可以访问当前节点
if (root.right == null || root.right == prev) {
tree.add(root.val);
//更新历史访问记录,这样回溯的时候父节点可以由此判断右子树是否访问完成
prev = root;
root = null;
} else {
//如果右子树没有被访问,那么将当前节点压栈,访问右子树
stack.push(root);
root = root.right;
}
}
return tree;
}
}