一、n皇后问题
1、概述
n皇后要求在一个n×n的棋盘上放置n个皇后,使得他们彼此不受攻击,皇后可以攻击同一行、同一列、同一斜线上的敌人,所以n皇后问题要求寻找在棋盘上放置这n个皇后的方案,使得任意两个皇后都不在同一行、同一列或同一斜线上。
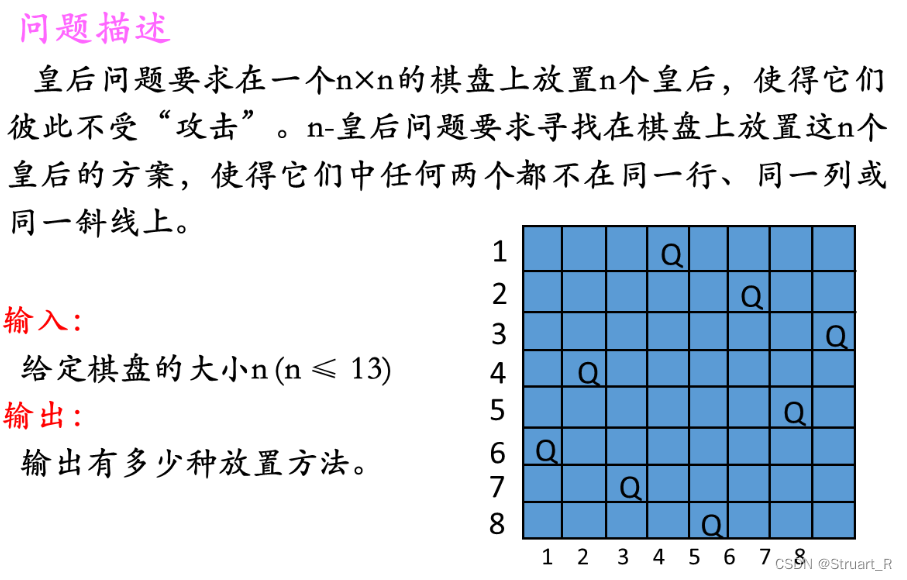
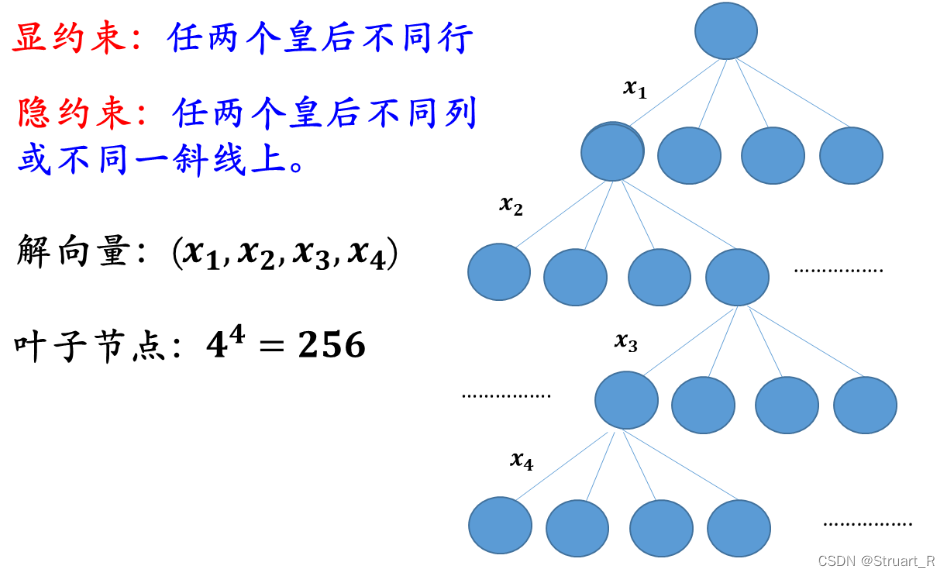
2、子集树解法
(1)判断是否遍历过叶子结点(t>n),若没有则遍历子集树,判断place(t),即该层从1到n是否存在有成立的情况。
(2)place剪枝函数,遍历1到t,如果存在一个点满足同一列,同一对角线,那么舍弃这个叶节点,反之保留叶节点。由于每一层保存的点存放在x数组,该数组显性约束了不满足同一行的条件,数组中的索引+1就是行号,数组值为列号。
(3)若已经满足t>n,即已经遍历过叶子结点,则输出该可行解。
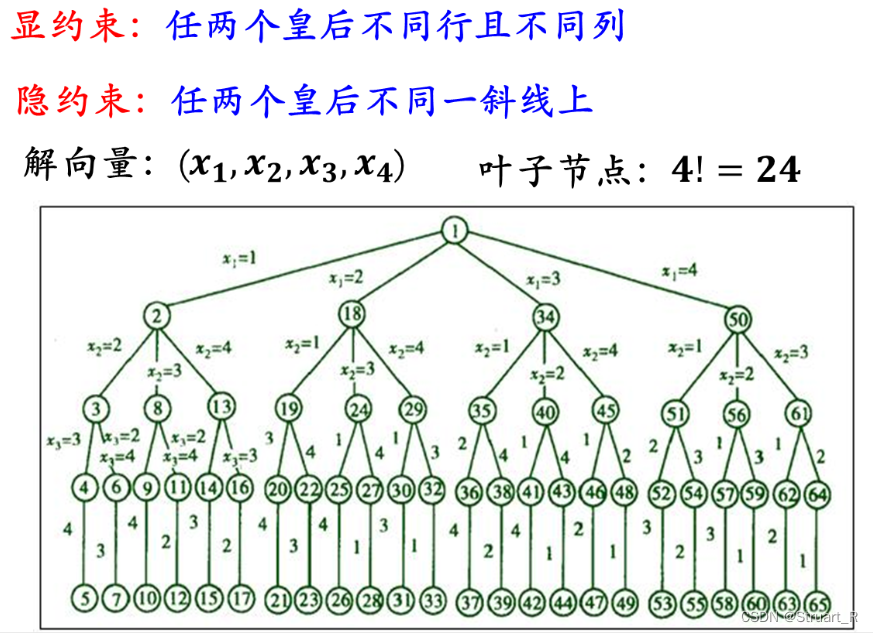
3、排列树解法
(1)判断是否遍历过叶子结点(t>n),若没有则遍历排列树,对后续层进行全排列,判断place(t),即该层从1到n是否存在有成立的情况。
(2)place剪枝函数,此时由于对后续层全排列,第一层的列数不能存在于后续层,不需要添加同一列的检查,其他与子集树一致。
(3)若已经满足t>n,即已经遍历过叶子结点,则输出该可行解。
4、代码
//n皇后问题
import java.util.Scanner;
public class Queen {
static int x[]=new int[100];
static int n;
static int sum=0;
public static void main(String [] args)
{
n=new Scanner(System.in).nextInt();
//排列树提前添加x数组值,保证能够进行排列
for(int i=1;i<=n;i++)
x[i]=i;
Backstack2(1);
}
//子集树算法
public static void Backstack(int t)
{
if(t>n)
{
sum++;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(x[i]==j)
System.out.print("Q ");
else
System.out.print(". ");
}
System.out.println();
}
System.out.println();
}
else
{
for(int i=1;i<=n;i++)
{
x[t]=i;
if(place(t))
Backstack(t+1);
}
}
}
public static boolean place(int t)
{
for(int i=1;i<t;i++)
if((Math.abs(x[i]-x[t])==Math.abs(i-t))||x[i]==x[t])
return false;
return true;
}
//排列树算法
public static void Backstack2(int t)
{
if(t>n)
{
sum++;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(x[i]==j)
System.out.print("Q ");
else
System.out.print(". ");
}
System.out.println();
}
System.out.println();
}
else{
for(int i=t;i<=n;i++)
{
swap(i,t);
if(place2(t))
Backstack2(t+1);
swap(i,t);
}
}
}
public static void swap(int i,int t)
{
int tmp=x[i];
x[i]=x[t];
x[t]=tmp;
}
public static boolean place2(int t)
{
for(int i=1;i<t;i++)
{
if(Math.abs(x[i]-x[t])==Math.abs(i-t))
return false;
}
return true;
}
}
5、结果
通过Q和 . 区分皇后的位置。

二、含重复元素的全排列
1、概述
给定一个可包含重复数字的序列,按任意顺序返回所有不重复的全排列,如:输入【1,1,2】,输出【1,1,2】,【1,2,1】,【2,1,1】。
2、算法
排列树问题,在原有问题上添加条件x[t]==x[i]&&t!=i,当前交换的两个数若相同,且不是同一个数,则剪枝,注意循环中使用continue,表示下面的交换和扩展的操作不再进行,但循环继续。
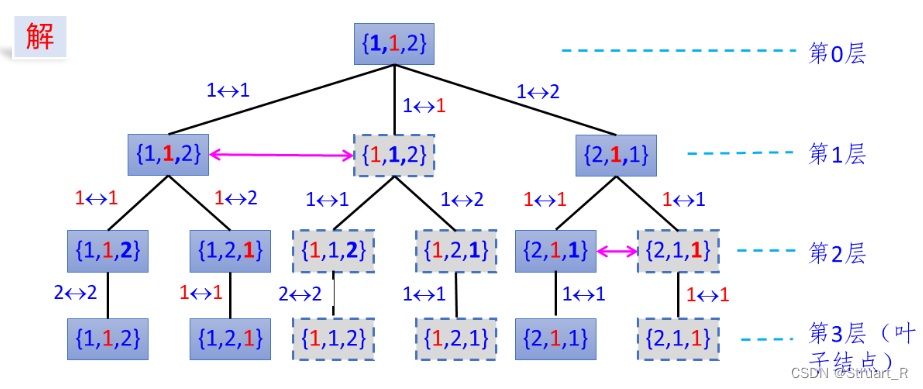
3、代码
//含重复元素的全排列
import java.util.Scanner;
public class repeatperm {
public static void main(String []args)
{
String m=new Scanner(System.in).nextLine();
String []numbers=m.split("\\s+");
int x[]=new int[numbers.length+1];
for(int i=0;i<numbers.length;i++)
x[i+1]=Integer.parseInt(numbers[i]);
perm(x,1);
}
//全排列
public static void perm(int[] x,int t)
{
int n=x.length-1;
if(t>n)
{
for(int i=1;i<n+1;i++)
System.out.print(x[i]+" ");
System.out.println();
}
else
{
for(int i=t;i<n+1;i++)
{
//约束条件,保证不再重复
if(x[t]==x[i]&&t!=i)
continue;
swap(t,i,x);
perm(x,t+1);
swap(t,i,x);
}
}
}
public static void swap(int t,int i,int []x)
{
int tmp=x[i];
x[i]=x[t];
x[t]=tmp;
}
}
三、 组合
1、概述
输入n和k,从1~n中任意不放回抽取k个值的所有情况,输入n=4,k=2,输出【1,2】,【1,3】,【1,4】,【2,3】,【2,4】,【3,4】。
2、算法
子集树,在叶子结点未遍历结束前,每一层的值都为上一层的节点值到n之间所有的遍历。
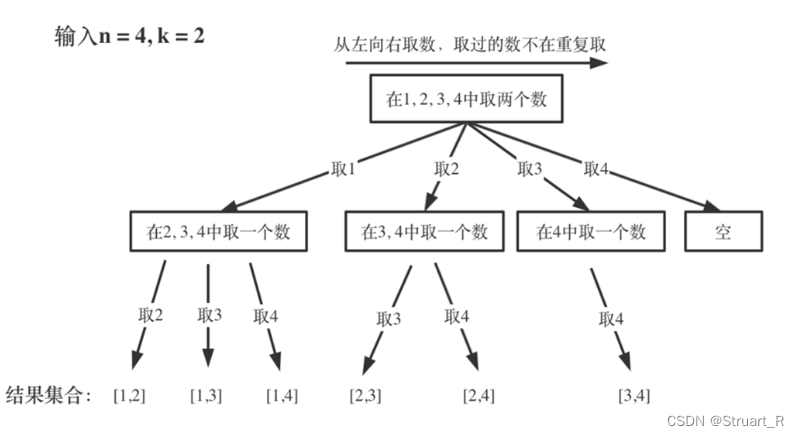
3、代码
//组合问题
import java.util.Scanner;
public class combination {
public static void main(String[] args)
{
int n=new Scanner(System.in).nextInt(); //n=4
int k=new Scanner(System.in).nextInt(); //k=2
int x[]=new int [k+1];
combine(n,k,1,x);
}
public static void combine(int n,int k,int t,int x[])
{
if(t>k)
{
for(int i=1;i<=k;i++)
System.out.print(x[i]+" ");
System.out.println();
}
else
{
for(int i=x[t-1]+1;i<=n;i++)
{
x[t]=i;
combine(n,k,t+1,x);
}
}
}
}四、组合总和
1、概述
输入n和k,输出1-9的任取k个数的组合中,组合加和等于n的所有可能情况。
2、算法
子集树算法,与上一道题相同,只需要在输出的时候,添加限制总和等于n的输出。另外可以进行改进,对于问题规模过大的情况,如果未完成的组合,组合总和已经大于等于n,则进行剪枝。
3、代码
//组合总和
import java.util.Scanner;
public class combinationsum {
public static void main(String[] args)
{
int n=new Scanner(System.in).nextInt(); //n=7,判断条件和
int k=new Scanner(System.in).nextInt(); //k=3
int x[]=new int [k+1];
combine(n,k,1,x);
}
public static void combine(int n,int k,int t,int x[])
{
if(t>k)
{
int sum=0;
for(int j:x)
sum+=j;
if(sum==n)
{
for(int i=1;i<=k;i++)
System.out.print(x[i]+" ");
System.out.println();
}
}
else
{
for(int i=x[t-1]+1;i<=9;i++)
{
x[t]=i;
combine(n,k,t+1,x);
}
}
}
}