目录

 

介绍：

代码： 

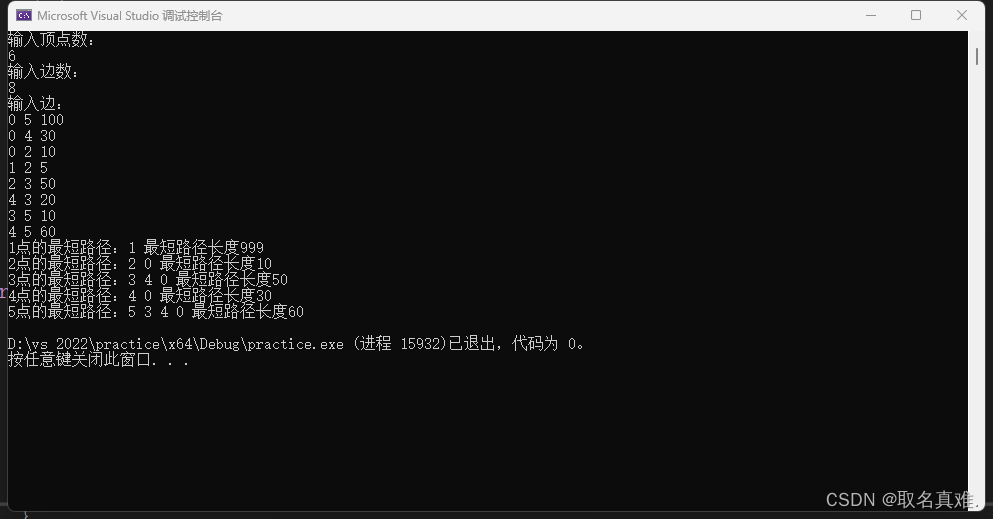
结果：

介绍：

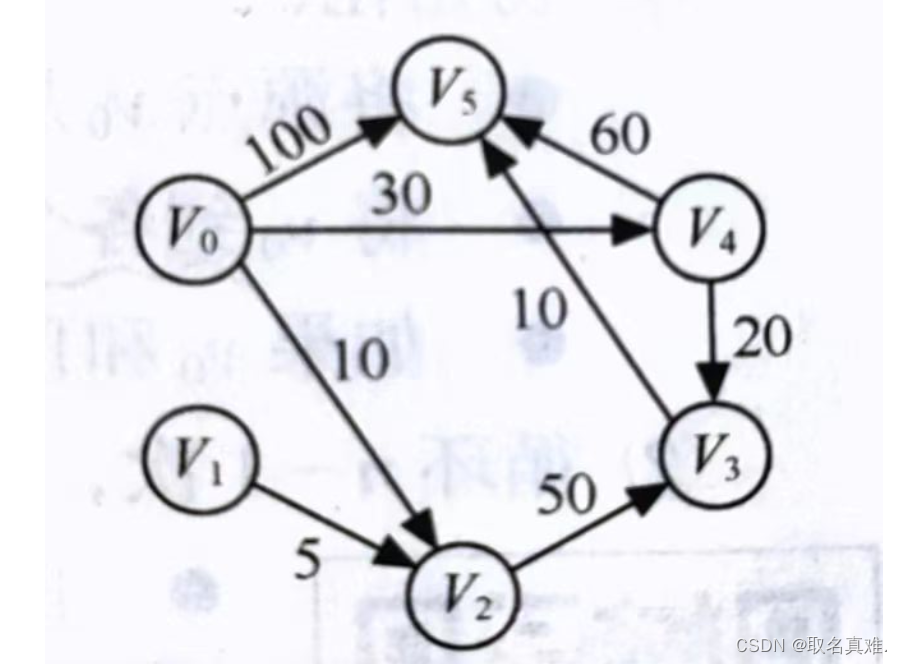
迪杰斯特拉算法（Dijkstra's algorithm）是一种用于计算加权图的单点最短路径的算法。它是由荷兰计算机科学家Edsger W. Dijkstra在1956年发明的。

该算法的思路是，从给定源点开始，不断找到距离该点最近的未访问节点，标记这个节点为已访问，并更新与该节点相邻的节点的最短路径。通过这样不断扩大已访问节点的范围，最终可以求出源点到其他所有节点的最短路径。

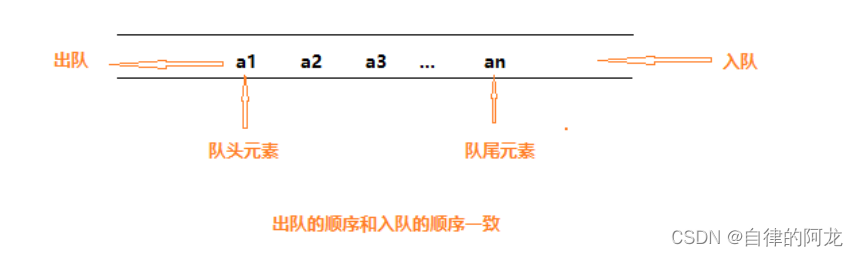
具体实现时，可以使用一个优先队列来保存即将访问的节点，优先队列中的元素按照节点与源点的距离从小到大排序，每次取出距离最小的节点进行访问。

迪杰斯特拉算法的复杂度为O(E log V)，其中E为边的数量，V为节点的数量。虽然该算法是一个贪心算法，并不能保证一定找到最优解，但对于大多数实际应用场景而言，其效率和正确性都已经得到了充分的验证。

 

代码： 

#include<iostream>
using namespace std;
int G[100][100], n, maxint=999, min1, v;
int s[100],d[100],path[100];//集合s代表已经找到最短路径的点
void DIJ(int v0)//迪杰斯特拉算法,从v0点到任意点的最短路径
{
	for (int i = 0; i < n; i++)//初始化
	{
		s[i] = 0;//视为空集
		d[i] = G[v0][i];//初始最短路径为v0到个点的权值
		if (d[i] < maxint)//v0与i之间有弧，则前驱设为v0
			path[i] = v0;
		else//v0与i之间无弧，则前驱设为-1
			path[i] = -1;
	}
	s[v0] = 1;//将v0加入集合s
	d[v0] = 0;//源点到源点距离为0
	for (int i = 1; i < n; i++)//访问剩下的n-1个点
	{
		min1 = maxint;
		for (int j = 0; j < n; j++)
		{
			if (!s[j] && d[j] < min1)//点不在集合s内且小于最小边
			{
				v = j;//选择一条当前最短路径，终点为v
				min1 = d[j];
			}
		}
		s[v] = 1;//将v加入集合s
		for (int j = 0; j < n; j++)//将v加入集合后，更新从v0到剩余点的最短路
		{
			if (!s[j] && (d[v] + G[v][j]) < d[j])//该点不在集合s内且加入v点后最短路径小于之前的最短路径
			{
				d[j] = d[v] + G[v][j];//更新最短路径
				path[j] = v;//前驱设为v
			}
		}
	}
	for (int i = 1; i < n; i++)//访问各点的最短路径
	{
		int t = path[i];
		cout << i << "点的最短路径："<<i<<" ";
		while (t != -1)
		{
			cout << t << " ";
			t = path[t];
		}
		cout << "最短路径长度"<<d[i];
		cout << endl;
	}
}
int main()
{
	cout << "输入顶点数：" << endl;
	cin >> n;
	for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++)
			 G[i][j] = maxint;
	cout << "输入边数：" << endl;
	int e;
	cin >> e;
	cout << "输入边：" << endl;
	for (int i = 1; i <= e; i++)
	{
		int v1, v2, w;
		cin >> v1 >> v2 >> w;
		G[v1][v2] = w;
	}
	DIJ(0);//从0号点到任意点的最短路径
}

结果：