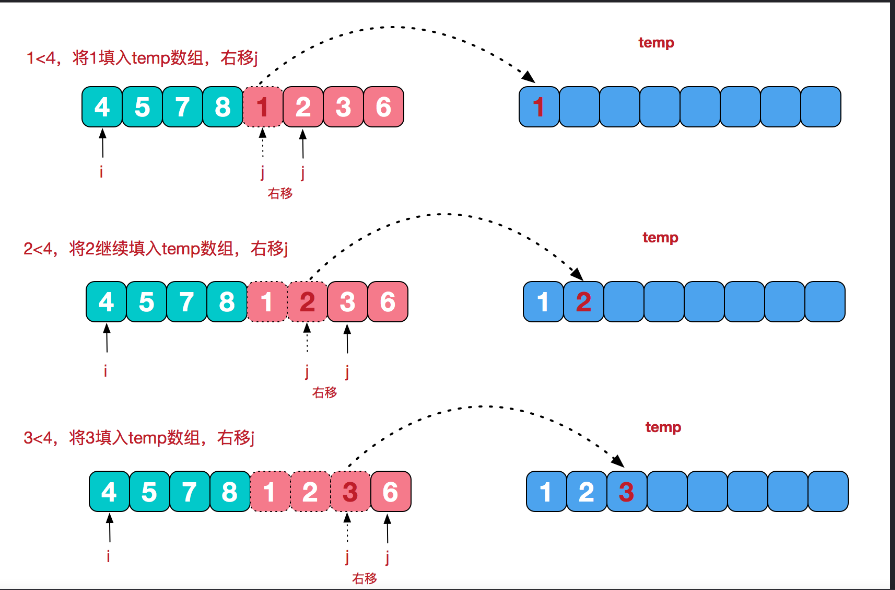
✏️✏️✏️今天给各位带来的是哈希桶、哈希冲突方面的知识。

清风的CSDN博客

😛😛😛希望我的文章能对你有所帮助，有不足的地方还请各位看官多多指教，大家一起学习交流！

动动你们发财的小手，点点关注点点赞！在此谢过啦！哈哈哈！😛😛😛

目录

 一、哈希表

1.1 概念

1.2 冲突

1.2.1 冲突概念

1.2.2 冲突避免 

1.2.3 冲突避免-哈希函数设计 

1.2.4 负载因子调节 

1.2.5 冲突解决-闭散列

 1.2.6 冲突解决-开散列

 1.2.7 哈希桶K-V型实现

1.3 性能分析 

---

 一、哈希表

1.1 概念

 当向该结构中：

• 插入元素：根据待插入元素的关键码，以此函数计算出该元素的存储位置并按此位置进行存放
• 搜索元素：对元素的关键码进行同样的计算，把求得的函数值当做元素的存储位置，在结构中按此位置取元素比较，若关键码相等，则搜索成功。

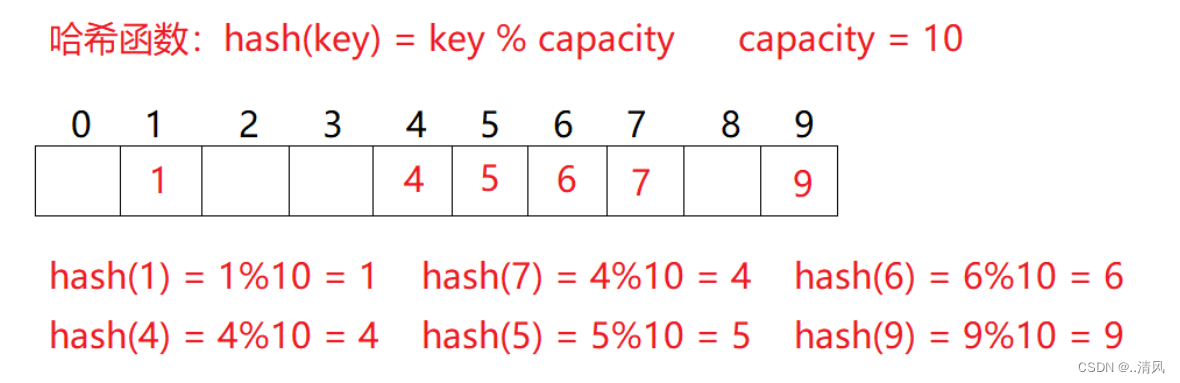
1.2 冲突

1.2.1 冲突概念

1.2.2 冲突避免 

1.2.3 冲突避免-哈希函数设计 

常见哈希函数： 

折叠法 

折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些)，然后将这几部分叠加求和，并按散列表表长，取后几位作为散列地址。 折叠法适合事先不需要知道关键字的分布，适合关键字位数比较多的情况  。 

数学分析法 

注意：哈希函数设计的越精妙，产生哈希冲突的可能性就越低，但是无法避免哈希冲突 。

1.2.4 负载因子调节 

 负载因子和冲突率的关系粗略演示：

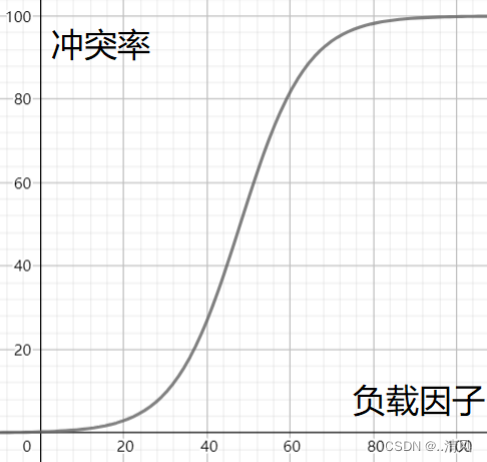
 所以当冲突率达到一个无法忍受的程度时，我们需要通过降低负载因子来变相的降低冲突率。已知哈希表中已有的关键字个数是不可变的，那我们能调整的就只有哈希表中的数组的大小。

1.2.5 冲突解决-闭散列

 解决哈希冲突两种常见的方法是：开散列和闭散列。

闭散列： 

•  线性探测：比如上面的场景，现在需要插入元素44，先通过哈希函数计算哈希地址，下标为4，因此44理论上应该插在该位置，但是该位置已经放了值为4的元素，即发生哈希冲突。那么就从发生冲突的位置开始，依次向后探测，直到寻找到下一个空位置为止。

• 二次探测  

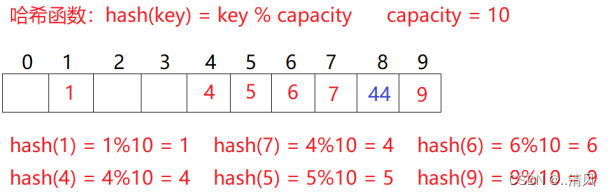
因此：闭散列最大的缺陷就是空间利用率比较低，这也是哈希的缺陷。

 1.2.6 冲突解决-开散列

 从上图可以看出，开散列中每个桶中放的都是发生哈希冲突的元素。 开散列，可以认为是把一个在大集合中的搜索问题转化为在小集合中做搜索了。

•  每个桶的背后是另一个哈希表
• 每个桶的背后是一棵搜索树

 1.2.7 哈希桶K-V型实现

类的基本定义：

public class Hash_Map<K,V> {

    static  class Node<K,V>{
        public K key;
        public V val;
        public Node<K,V> next;

        public Node(K key, V val) {
            this.key = key;
            this.val = val;
        }
    }

    public Node<K,V>[] array;
    public int usedSize;//记录当前存放的元素个数
    public static final float DEFAULT_LOAD_FACTOR = 0.75f;//默认负载因子

    public Hash_Map(){
        array=(Node<K, V>[]) new Node[10];
    }
}

存放元素：

    public void put(K key, V val){
        int hash = key.hashCode();
        int index = hash % array.length;
        Node<K,V> cur = array[index];
        while (cur!=null){
            if(cur.key.equals(key)){
                cur.val=val;
                return;
            }
            cur = cur.next;
        }
        Node<K,V> node = new Node<>(key,val);
        node.next=array[index];
        array[index]=node;
        usedSize++;
        if(doLOAD_FACTOR()>DEFAULT_LOAD_FACTOR){
            resize();
        }
    }
    //计算当前负载因子
    private float doLOAD_FACTOR(){
        return usedSize*1.0f / array.length;
    }  
    //如果哈希桶已满，扩容后重新哈希
    private void resize(){
        Node<K,V>[] newArray = new Node[array.length*2];
        for (int i = 0; i < array.length; i++) {
            Node<K,V> cur = array[i];
            while (cur!=null){
                //先生成整数，调用hashCode
                Node<K,V> curNext = cur.next;
                int newHash = cur.key.hashCode();
                int newIndex = newHash % newArray.length;
                cur.next = newArray[newIndex];
                cur = curNext;
            }
        }
        array = newArray;
    }

获取key位置的val值：

    public V getValue(K key){
        int hash = key.hashCode();
        int index = hash % array.length;
        Node<K,V> cur = array[index];
        while (cur!=null){
            if(cur.key.equals(key)){//引用类型不可使用等号比较!!!!!!
                return cur.val;
            }
            cur = cur.next;
        }
        return null;
    }

1.3 性能分析 

---

✨希望各位看官读完文章后，能够有所提升。

🎉好啦，今天的分享就到这里！！

✨创作不易，还希望各位大佬支持一下！

👍点赞，你的认可是我创作的动力！

⭐收藏，你的青睐是我努力的方向！

✏️评论：你的意见是我进步的财富！