审题要清楚：

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。注意是叶子节点（左右孩子都为空的节点才是叶子节点！）。

算法：

既可以求最小高度，也可以直接求深度。

最小高度：

后序遍历（找到叶子节点，然后从下往上求，LRV）

求深度：

前序遍历（从上往下查，VLR）

前序遍历更符合常规逻辑，但是代码稍微复杂一些，所以这里用后序遍历。

调试过程：

递归法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: Optional[TreeNode]) -> int:
        return self.getdepth(root)
    def getdepth(self, node: Optional[TreeNode]):
        #空节点，若root为空，空树
        if node == None:
            return 0
        else:
        #求左右子树的高度
            leftheight = self.getdepth(node.left)
            rightheight = self.getdepth(node.right)
        #排除只有左子树或右子树单个子树为空的情况
            if node.left == None and node.right != None:
                #返回值还要加上父节点的高度
                return 1+rightheight
            if node.right == None and node.left != None:
                #返回值还要加上父节点的高度
                return 1+leftheight
            elif node.right != None and node.left != None:
                return 1+min(leftheight,rightheight)
                
        

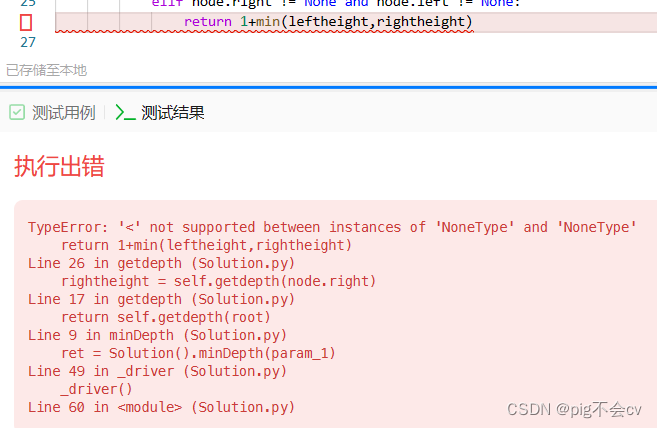
原因：

尝试使用`<`运算符比较两个`None`值，而在Python中这是不允许的。

在你的代码中，错误发生在`return 1+min(leftheight,rightheight)`这一行，当`leftheight`和`rightheight`都是`None`时。这种情况发生在一个节点既没有左子节点也没有右子节点的情况下。

正确代码：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: Optional[TreeNode]) -> int:
        return self.getdepth(root)
    def getdepth(self, node: Optional[TreeNode]):
        #空节点，若root为空，空树
        if node == None:
            return 0
        else:
        #求左右子树的高度
            leftheight = self.getdepth(node.left)
            rightheight = self.getdepth(node.right)
        #排除只有左子树或右子树单个子树为空的情况
            if node.left == None and node.right != None:
                #返回值还要加上父节点的高度
                return 1+rightheight
            if node.right == None and node.left != None:
                #返回值还要加上父节点的高度
                return 1+leftheight
            
            return 1+min(leftheight,rightheight)
                
        

时间空间复杂度：

时间复杂度分析：

• 在最坏情况下，需要遍历二叉树的所有节点才能确定最小深度。因此，时间复杂度为O(n)，其中n是二叉树中的节点数。

空间复杂度分析：

• 递归调用的空间复杂度取决于递归的深度，即树的高度。在最坏情况下，二叉树是一个链表结构，高度为n。因此，递归调用的空间复杂度为O(n)。
• 此外，除了递归调用的空间，没有使用额外的数据结构。因此，除了递归调用的空间外，空间复杂度为O(1)。

综上所述，时间复杂度为O(n)，空间复杂度为O(n)（由于递归调用的空间）或O(1)（除了递归调用的空间）。