简单线性回归函数
- 定义
- 术语
- 理解
- 简单线性回归例子
定义
线性回归:利用线性回归方程中最小平方函数对一个或多个自变量和因变量之间关系进行建模的一个回归分析。该建模的目标为找到各个系数的最佳值让预测误差最小
简单线性回归:只有一个自变量的线性回归
公式: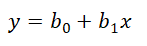
多元线性回归:大于一个自变量的线性回归
术语
自变量:因变量发生变化的原因,函数中的x
因变量:自变量发生变化的结果,函数中的y
截距:直线与y轴相交的位置与原点的距离,函数中的b0
斜率:直线的倾斜程度,函数中的b1
均方根误差:又称为标准误差,用于测量预测值与真实值偏差RMSE
决定系数:能够由自变量解释的变异程度占总的变异程度的比例符号为R2
简单线性回归算法步骤
算法步骤
计算x与y的平均值:将所有的x或y求和并除去其数量
计算x与y较其平均值的误差e: 将每一个x,y值减去他们的平均值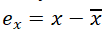
计算x,y误差的平方: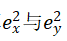
计算误差乘积和:xy误差乘积和: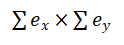
计算斜率b1: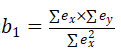
计算截距b0: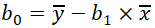
计算误差RMSE:将训练集中的x代入,分别求解y并减去实际y获得误差。将误差相乘获得乘积除以n个样本容易获得RMSE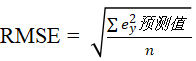
理解
计算误差R2:将实际的y值误差平方的求和除以用线性回归公式求出的y值误差平方的求和
简单线性回归例子
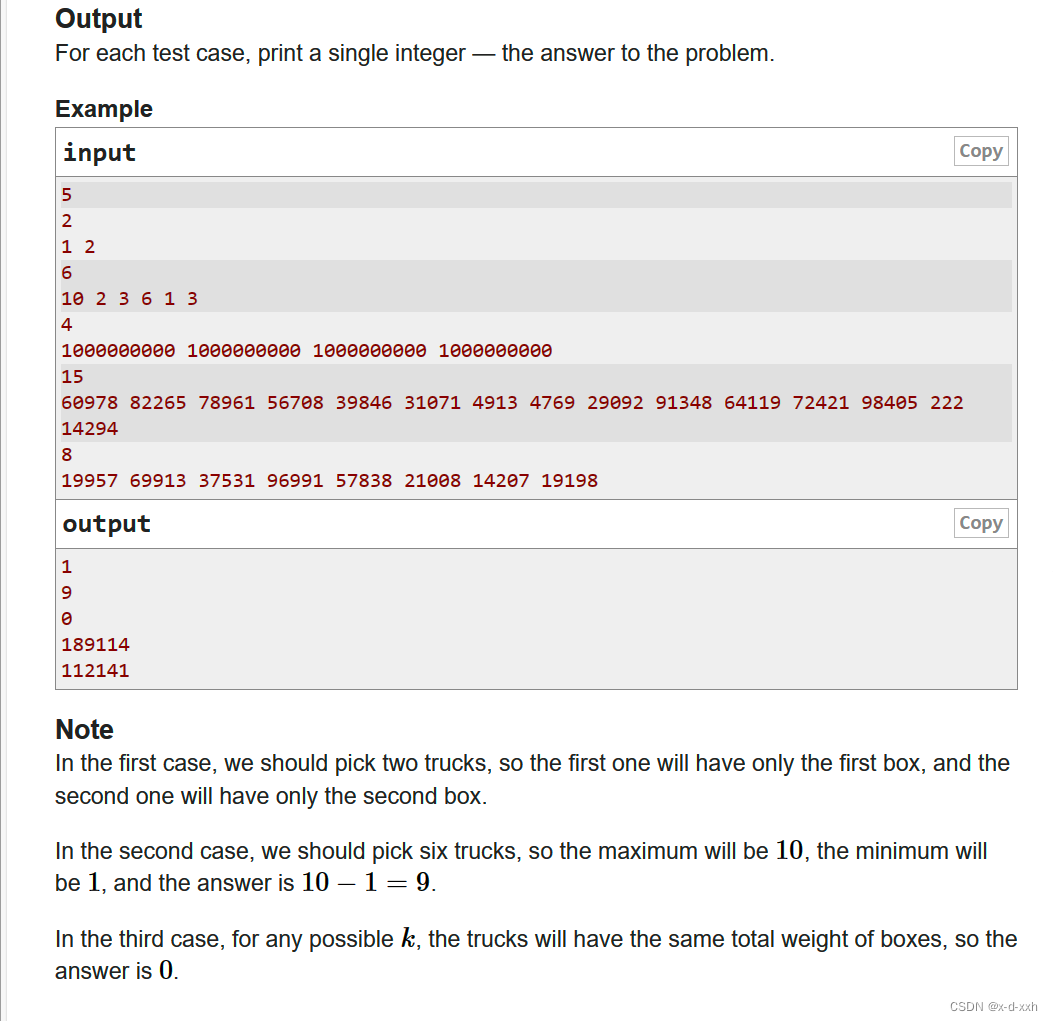
题目1,根据下列图表求出简单线性回归公式,计算公式的标准误差以及决定系数。
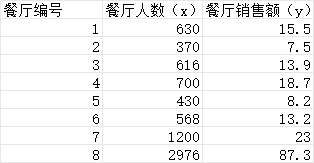
①计算x与y的平均值
②计算x与y较其平均值的误差e
③计算x,y误差的平方
④计算误差乘积和
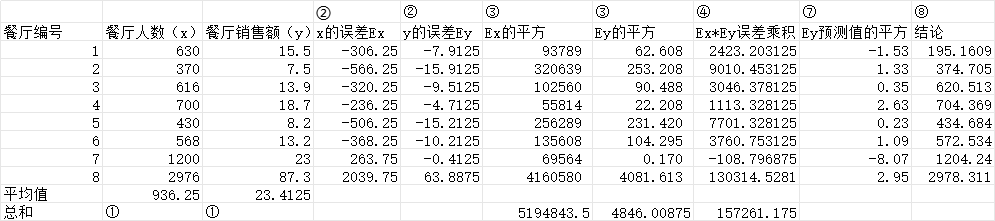
⑤计算斜率b1 =
⑥计算截距b0 =
⑦Ey预测值的平方 Ey
⑧根据以上得出公式y = -4.93+0.03*x
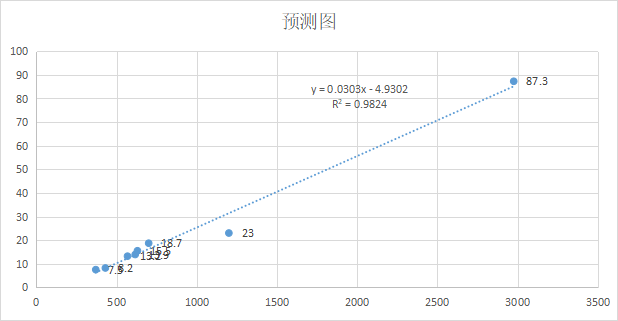




![【算法每日一练]-图论(保姆级教程 篇4(遍历))#传送门 #负环判断 #灾后重建](https://img-blog.csdnimg.cn/7a8e80cbfd4943008e3982646f5e96a2.png)