今天继续
目录
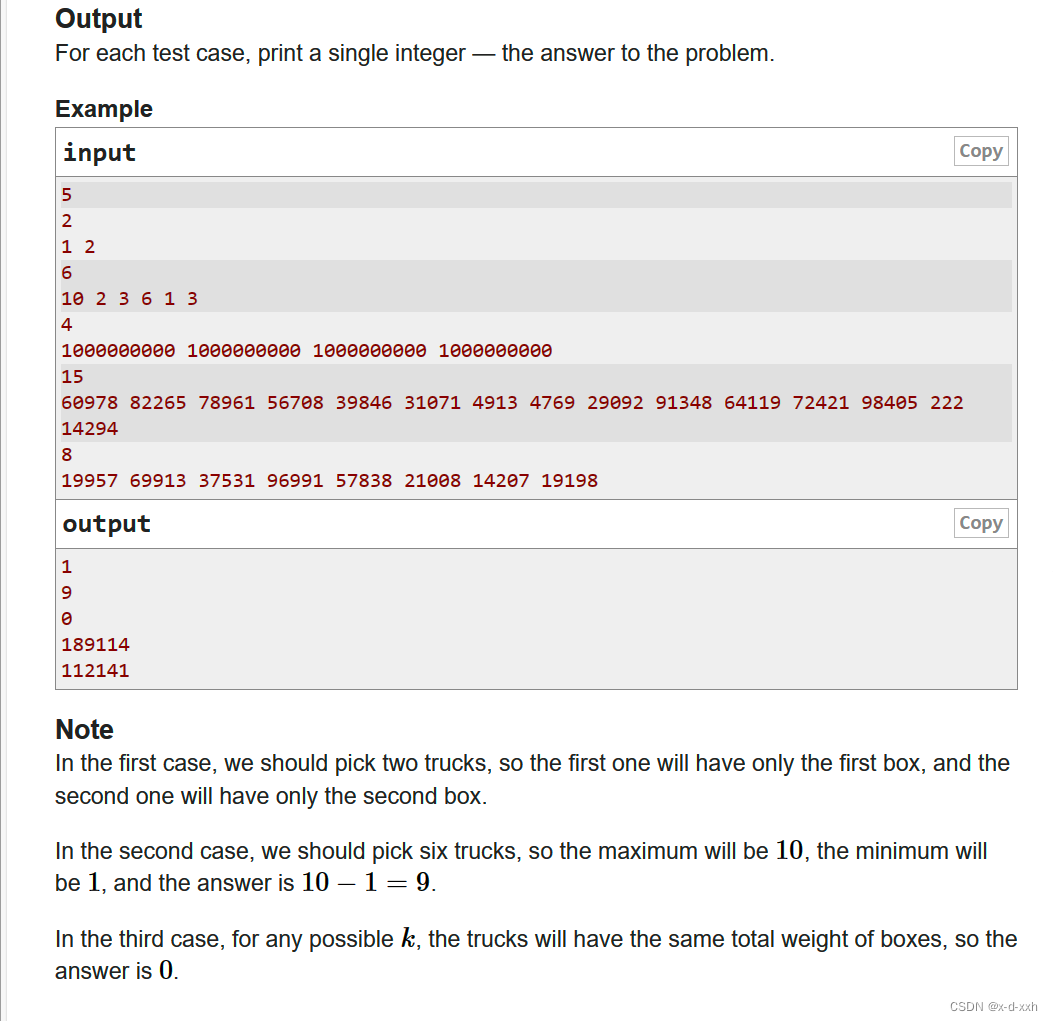
题目:传送门
思路:
题目:负环判断
思路:
题目:灾后重建
思路:
题目:传送 门

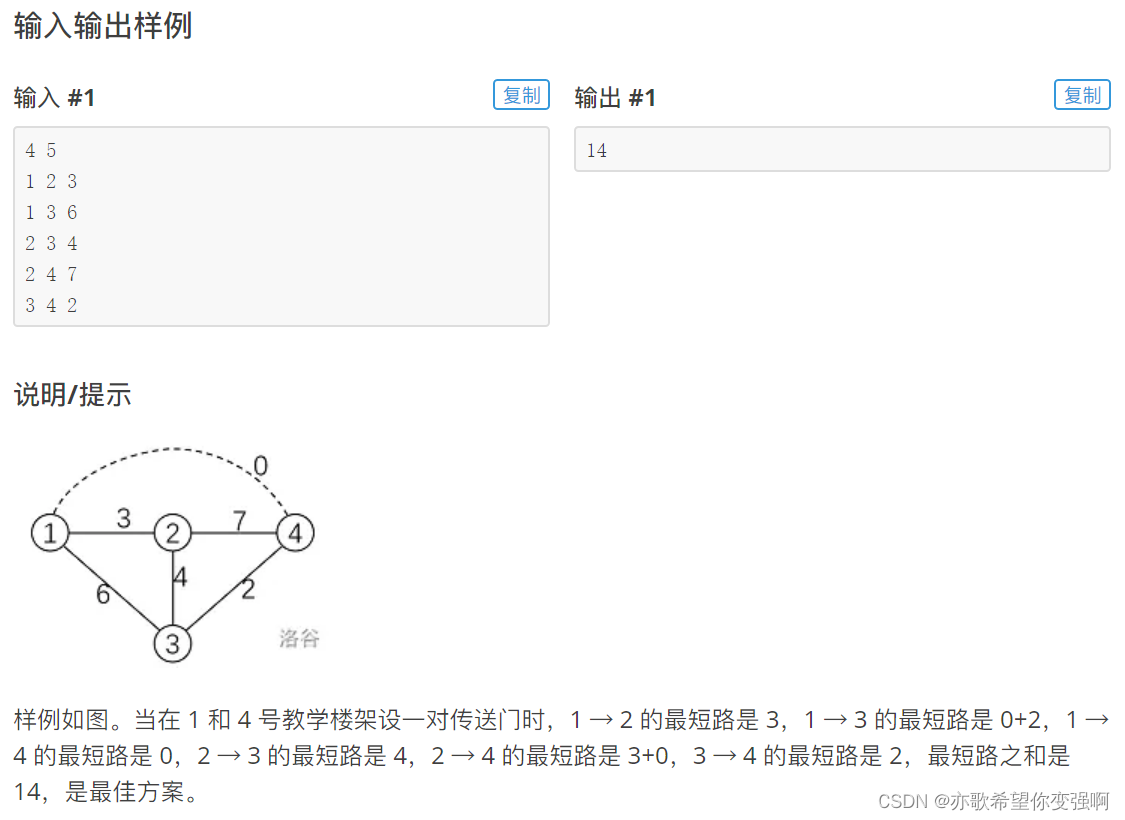
思路:
先跑一边floyd,然后依次加入每个传送门,O(n^5)不行。
所以不能跑n^2次floyd,应该单独把两个有影响的点摘出来处理dis,降为O(n^4)能过
#include <bits/stdc++.h>
using namespace std;
const int N=105;
int n,m,f1[N][N],f2[N][N];
inline void back(){
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
f1[i][j]=f2[i][j];
}
}
int main(){
cin>>n>>m;int u,v,w,ans=1e9;
memset(f1,0x3f,sizeof(f1));
for(int i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
f1[u][v]=w;f1[v][u]=w;
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
f1[i][j]=min(f1[i][k]+f1[k][j],f1[i][j]);
f2[i][j]=f1[i][j];
}
for(int i=1;i<=n;i++)
for(int j=1;j<i;j++){//枚举每个传送门
f1[i][j]=f1[j][i]=0;
for(int k1=1;k1<=n;k1++)
for(int k2=1;k2<=n;k2++)
f1[k1][k2]=min(f1[k1][k2],f1[k1][i]+f1[i][k2]);//由i点进行中转
for(int k1=1;k1<=n;k1++)
for(int k2=1;k2<=n;k2++)
f1[k1][k2]=min(f1[k1][k2],f1[k1][j]+f1[j][k2]);//由i,j点进行中转
int tmp=0;
for(int k1=1;k1<=n;k1++)//这里因为我们没有初始化对角线,所以不要加对角线元素
for(int k2=1;k2<k1;k2++)//把根据无向图的对称型即可
tmp+=f1[k1][k2];
ans=min(ans,tmp);
back();
}
cout<<ans;
return 0;
}
题目:负环判断

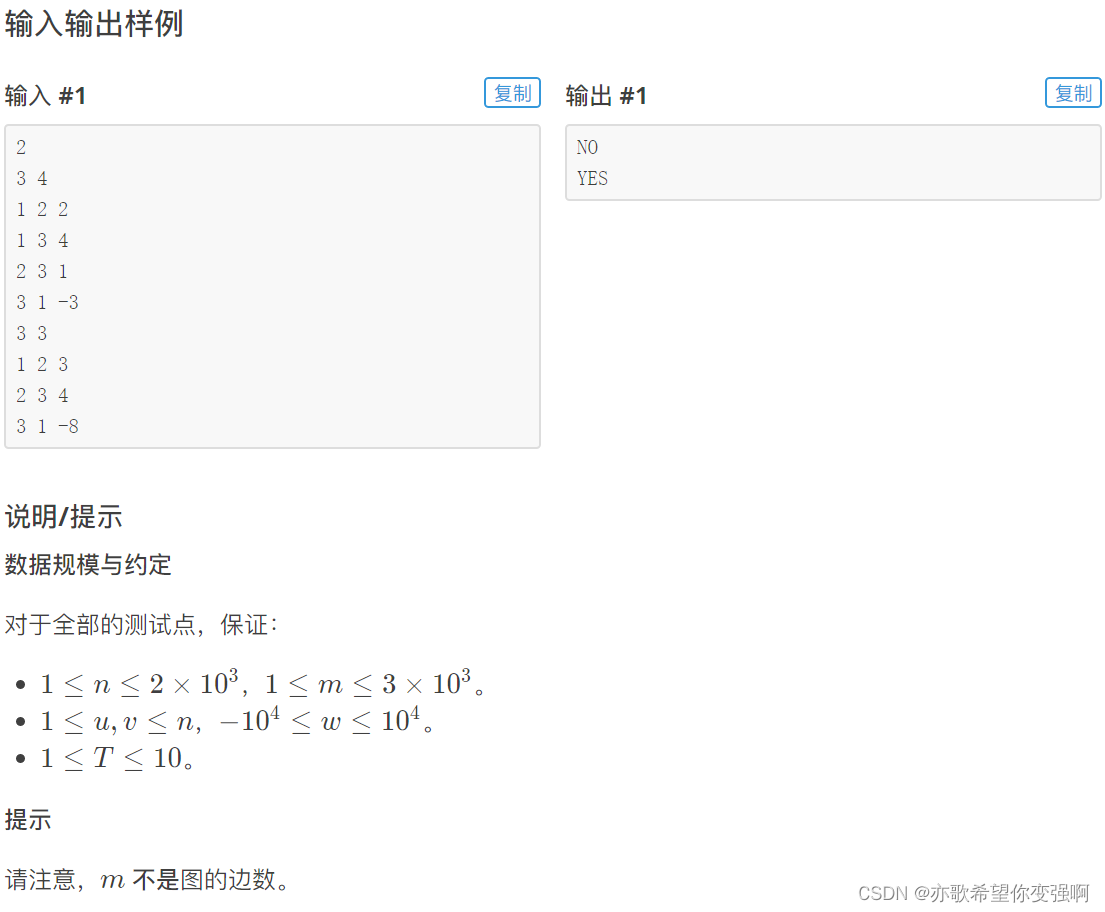
思路:
只需要记录最短路长度即可,这个长度不是带权的长度,是经过的点个数 如果长度大于n一定有问题,也就是出现了负环,如果不停止就会走向无穷小
#include <bits/stdc++.h>
using namespace std;
const int N=2005,M=3005;
int n,m,tot;
queue<int>q;
int head[N],vis[N],dis[N],cnt[N];//dis存放到每个点的最短距离,cnt存放对应的长度
struct node{int to;int w;int next;}e[M*2];
void add(int u,int v,int w){e[++tot]=(node){v,w,head[u]};head[u]=tot;}
int spfa(){//判断负环的spfa
memset(dis,0x3f,sizeof(dis));
memset(cnt,0,sizeof(cnt));
memset(vis,0,sizeof(vis));
while(!q.empty()) q.pop();//要把队列清空(c++不支持队列清空函数)
dis[1]=0;vis[1]=1;q.push(1);
while(!q.empty()){
int cur=q.front();q.pop();
vis[cur]=0;
for(int i=head[cur];i;i=e[i].next){
int v=e[i].to,w=e[i].w;
if(dis[cur]+w<dis[v]){
dis[v]=dis[cur]+w;
cnt[v]=cnt[cur]+1//记录最短路长度;
if(cnt[v]>n)return 1;//如果长度大于n一定有问题,也就是出现了负环,如果不停止就会走向无穷小
if(!vis[v])q.push(v),vis[v]=1;
}
}
}
return 0;
}
int main(){
int t,u,v,w;
cin>>t;
while(t--){
tot=0;memset(head,0,sizeof(head));
cin>>n>>m;
for(int i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
if(w>=0)add(v,u,w);
}
if(spfa())cout<<"YES"<<'\n';
else cout<<"NO"<<'\n';
}
}
题目:灾后重建


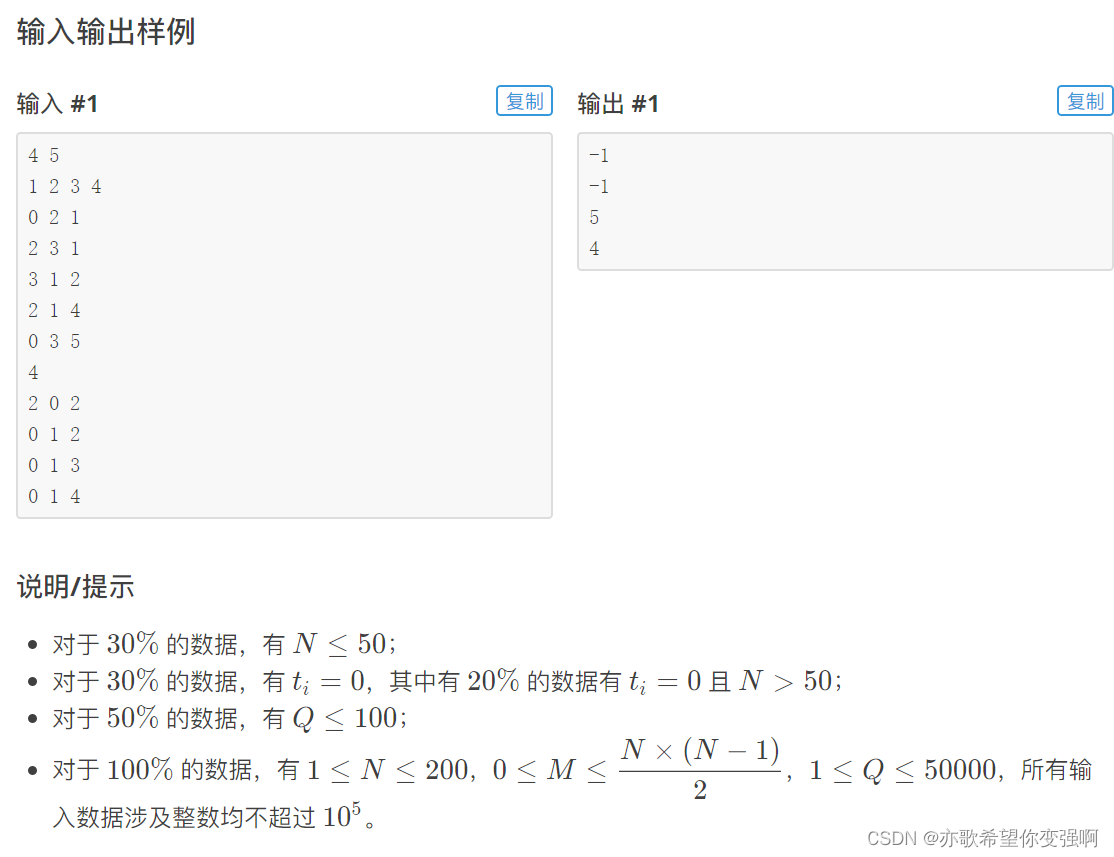
思路:
floyd的最外层k其实是在放入前k个点后的对dis的影响
eg:k为1是仅放入1对dis的影响,k为2是仅放入1和2后对dis的影响,依次类推
那么此题,我们只需要放一个对应的点,就输出一次,这就是前k个点的影响
#include <bits/stdc++.h>
using namespace std;
const int N=205;
int n,m,INF;
int a[N],f[N][N];
inline void updata(int k){//依次放入k,对各个dis进行影响
for(int i=0;i<n;i++)
for(int j=0;j<n;j++){
if(f[i][j]>f[i][k]+f[k][j])
f[i][j]=f[i][k]+f[k][j];
}
}
int main(){
cin>>n>>m;
for(int i=0;i<n;i++) cin>>a[i];//每个村庄的建好时间
memset(f,0x3f,sizeof(f));INF=f[1][1];//初始化f
for(int i=0;i<n;i++) f[i][i]=0;
int u,v,w;
for(int i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
f[u][v]=f[v][u]=w;
}
int q,t,now=0;cin>>q;
while(q--){
cin>>u>>v>>t;//询问
while(a[now]<=t&&now<n){//把t时间之前的村庄都考虑进去
updata(now);now++;
}
if(a[u]>t||a[v]>t)cout<<-1<<'\n';//村庄还没修好
else{
if(f[u][v]==INF)cout<<-1<<'\n';//根本就无法到达
else cout<<f[u][v]<<'\n';
}
}
return 0;
}