在我的上一篇文章中，我们介绍了用于数据分析和清理的不同技术，以准备用于预测的数据。在完成数据的分析和提炼后，我们成功实现了获得不存在任何缺失值、异常值或其他异常的原始数据集的目标。

        现在，我们将继续使用上一篇文章中准备的相同数据集，并探索预测过程中的进一步步骤。

二、训练测试分割

        让我们在测试和训练之间分割数据。我们将使用 85% 的数据作为训练数据，其余作为测试数据。

        这样，我们就成功地将数据分为训练子集和测试子集。我们将在下面的预测方法中使用这些子集。

三、预测方法一：简单移动平均线

        简单移动平均线（SMA）是时间序列预测的常用方法。它是一种统计技术，计算指定数量的周期或时间间隔内的序列的平均值。SMA 方法假设过去的值代表未来的模式，并使用此假设来预测未来的值

在上面的代码中，我采用了 6 个月的移动平均窗口。下面是测试、训练和预测数据集的图。

        现在，让我们检查错误以评估准确性。

        该模型的准确度低于 50%，这意味着它不是该数据集的良好模型。值得注意的是，SMA 方法是一种简单直观的方法，但它有一些局限性。它可能无法捕获底层数据的复杂模式或变化。此外，它对窗口内的所有数据点给予相同的权重，这可能并不适合所有时间序列。其他高级方法（如指数平滑、ARIMA 或机器学习算法）可用于克服这些限制并提供更准确的预测。

四、预测方法 2：简单指数平滑

        简单指数平滑 (SES) 是一种基本的时间序列预测方法，它为过去的观测值分配指数递减的权重。

        考虑下面的代码。这里我们从 statsmodel 包中导入 SimpleExpSmoothing 来创建模型

上面我使用了 0.001 的平滑级别来获得最佳精度。下面是测试、训练和预测数据集的图。

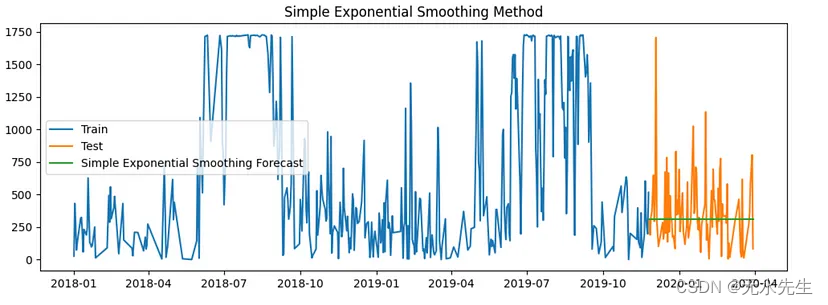
        现在，让我们检查错误以评估准确性。

        该模型的准确率约为 53.2%，这肯定比以前更好，但仍然不是一个好的模型。

五、预测方法 3：季节性自回归综合移动平均线 (SARIMA)

        SARIMA，全称季节性自回归综合移动平均线，是一种将 ARIMA 模型与季节性相结合的时间序列预测模型。它是 ARIMA 模型的扩展，旨在处理呈现季节性模式的时间序列数据。

        ARIMA 模型对于预测平稳时间序列数据（均值和方差恒定的数据）非常有效。然而，许多现实世界的时间序列都表现出季节性，即模式定期重复，例如每天、每月或每年。SARIMA 通过将季节性差异和季节性成分纳入 ARIMA 模型来解决此问题。

5.1 确认平稳性

        为了确认时间序列数据的平稳性，有两种常用的方法：Augmented Dickey-Fuller (ADF) 检验和 Kwiatkowski-Phillips-Schmidt-Shin (KPSS) 检验。这些检验检查平稳性的不同方面，并且可以在评估数据集的平稳性时相互补充。

1. 增强迪基-富勒 (ADF) 测试。ADF 检验检查是否存在单位根，表明非平稳性。如果 p 值低于选定的显着性水平，则该序列被视为平稳。

5.2 ADF测试

        上面代码中的dataFinal是我们在上一篇文章中准备的数据。该代码给出的p 值为0.016，小于临界值 0.05，这意味着根据此测试系列是平稳的

        2. Kwiatkowski-Phillips-Schmidt-Shin (KPSS) 检验：KPSS 检验侧重于平稳性的原假设。如果 p 值高于显着性水平，则该序列是平稳的。

5.3 KPSS测试

        该代码给出的p 值为0.1，该值大于临界值 0.05，这意味着零假设被拒绝，因此该序列是平稳的。

        现在让我们应用 SARIMA 方法来获取将用于拟合的模型参数

下面的输出显示了评估模型并提供参数的多个步骤。

让我们检查一下模型摘要。

        现在，有了模型参数，我们就可以拟合模型并对测试数据进行预测

        预测现已准备就绪，让我们绘制相同的图来检查训练和测试数据集的效果。

        上面看起来不错，比以前的型号更好。让我们检查模型的误差和准确性。

        该模型的准确率约为 98.5%，这使得该模型成为所有模型中准确率最高的。因此，这是我们可用于预测风力发电的最终模型。

六、结论

        我们对风电数据集的分析涉及测试三种不同的模型：简单移动平均线、简单指数平滑和 SARIMA。结果显示模型之间的准确性存在显着差异。

        简单移动平均法采用 6 个月的移动窗口，其准确度低于 50%。这种方法可能不适合捕获风力发电数据集中存在的复杂模式和波动。

        另一方面，简单指数平滑方法的表现稍好一些，准确率为 46%。虽然比简单移动平均线有所改进，但它在准确预测风电价值方面仍然存在不足。

        最后，SARIMA 模型表现出了最高的准确率，达到了令人印象深刻的 98.5%。该方法结合了季节性、自回归和移动平均成分，使其能够捕获时间序列数据中的固有模式和依赖性。

        值得注意的是，其他模型，例如基于 LSTM 模型的人工神经网络 (ANN) 或递归神经网络 (RNN) 模型，可能会提供更高的准确度，具体取决于具体用例和数据集的特征。这些模型以其捕获复杂关系和时间依赖性的能力而闻名，这使得它们特别适合时间序列分析。

        在未来的分析中，探索 ANN 或 LSTM 模型在风电数据集上的潜力是值得的，因为它们可以进一步提高准确性。然而，在选择最合适的建模方法之前，必须仔细评估数据的具体要求和特征。