目录
338比特位计数
题目要求:
解题思路:
1、暴力穷举
代码:
2、N&(N - 1)公式求解
代码:
3、奇偶数性质解法:
代码:
20有效的括号
题目要求:
解题思路
代码:
415字符串相加
题目要求
解题思路
代码:
338比特位计数
题目要求:
连接:338. 比特位计数 - 力扣(LeetCode)
给你一个整数
n,对于0 <= i <= n中的每个i,计算其二进制表示中1的个数 ,返回一个长度为n + 1的数组ans作为答案。示例 1:
输入:n = 2 输出:[0,1,1] 解释: 0 --> 0 1 --> 1 2 --> 10示例 2:
输入:n = 5 输出:[0,1,1,2,1,2] 解释: 0 --> 0 1 --> 1 2 --> 10 3 --> 11 4 --> 100 5 --> 101
解题思路:
1、暴力穷举
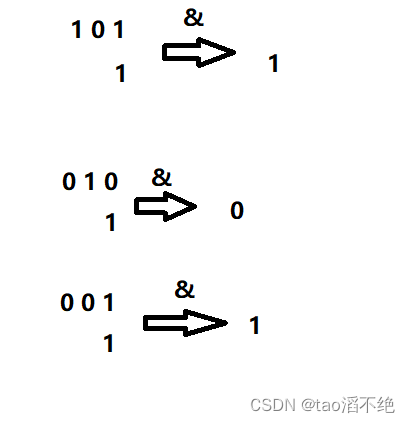
遍历一遍 1 到 n,把里面的元素按位与上一个1,如果等于1,则说明当前i的末尾是1,用计数器记录下来,不是则不记录下来,然后再右移1位,如图:
代码:
public int[] countBits(int n) { int[] array = new int[n + 1]; array[0] = 0; for(int i = 1; i <= n; i++) { int x = i; int count = 0; while(x > 0) { if((x & 1) == 1) { count++; } x >>= 1; } array[i] = count; } return array; }
2、N&(N - 1)公式求解
如图:
解释:如果我们求21的二进制1的个数,那么就可以求20的二进制1的个数 + 1,求20的二进制1的个数就可以求16的二进制1的个数 + 1,求16的二进制1的个数就可以求0的二进制1的个数 + 1,所以,我们得到求某一数字N的二进制1的个数:(N &(N - 1))+ 1
代码:
public int[] countBits(int n) {
int[] array = new int[n + 1];
array[0] = 0;
for(int i = 1; i < array.length; i++) {
array[i] = array[i & (i-1)] + 1;
}
return array;
}3、奇偶数性质解法:
如图:
i = 5,7时,是奇数,观察上图可以发现,他们的二进制1的个数是 i 的前一个下标4,5的二进制1的个数 + 1。
所以当 i 是奇数时,我们就算它前一个下标的二进制个数+1就好了。
我们可以发现,i 为偶数时,他们的二进制1的个数和 i 右移一位(或者除 2)的二进制1的个数一样。
所以 i 为偶数时,我们算它右移一位的数二进制1个个数就好了。
代码:
public int[] countBits(int n) {
int[] arr = new int[n + 1];
arr[0] = 0;
for(int i = 1; i < arr.length; i++) {
arr[i] = (i & 1) == 1 ? arr[i - 1] + 1 : arr[i >> 1];
}
return arr;
}20有效的括号
题目要求:
连接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
给定一个只包括
'(',')','{','}','[',']'的字符串s,判断字符串是否有效。有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = "()" 输出:true示例 2:
输入:s = "()[]{}" 输出:true示例 3:
输入:s = "(]" 输出:false
解题思路
利用栈的这种数据结构,对比前一个括号左是否和当前的右括号匹配,利用栈的先进后出的特性,当遇到一个左括号,就放进栈里面一个右括号,取到的字符是右括号时,就判断这个这个右括号和栈里的栈顶元素是否相等,不相等就返回false,相等就弹出,继续下一次判断,。字符串没遍历完,如果栈为空了,则是右括号多了,返回false,如果字符串遍历完了,但是栈不为空,则是左括号多了,返回false。
代码:
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for(char x : s.toCharArray()) {
if(x == '(') {
stack.push(')');
} else if(x == '[') {
stack.push(']');
} else if(x == '{') {
stack.push('}');
} else if(stack.empty() || stack.pop() != x) {
return false;
}
}
return stack.empty();
}415字符串相加
题目要求
连接:415. 字符串相加 - 力扣(LeetCode)
给定两个字符串形式的非负整数
num1和num2,计算它们的和并同样以字符串形式返回。你不能使用任何內建的用于处理大整数的库(比如
BigInteger), 也不能直接将输入的字符串转换为整数形式。示例 1:
输入:num1 = "11", num2 = "123" 输出:"134"示例 2:
输入:num1 = "456", num2 = "77" 输出:"533"示例 3:
输入:num1 = "0", num2 = "0" 输出:"0"提示:
1 <= num1.length, num2.length <= 104num1和num2都只包含数字0-9num1和num2都不包含任何前导零
解题思路
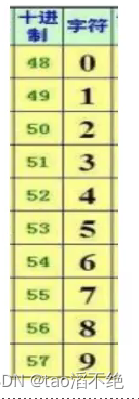
要把两个字符串数字相加,再放进字符串中,返回字符串类型,那么就需要把这两个字符串分别取出来,然后求出两字符串的长度 - 1,定义为下标,从后往前进行遍历(arr.length()),同时遍历他们,每次都要取出当前下标的字符,然后当前下标字符再减去'0'下标字符,就是这个字符的的整型数字了,ASCLL表如图
再定义一个进位遍历carry,拿到当前下标的两字符数字(x + y + carry),定义一个StringBuilder类型,把(x + y + carry)放进这个类里面,再和carry相加 % 10,
carry = (x + y +carry)/ 10,每遍历一次下标,都要执行以上操作,当字符串遍历完时,逆转这个字符串,再返回这个字符串。
代码:
public String addStrings(String num1, String num2) {
StringBuilder sb = new StringBuilder();
//记录进位的变量
int carry = 0;
//记录字符串的下标
int n1 = num1.length() - 1;
int n2 = num2.length() - 1;
for(; n1 >= 0 || n2 >= 0 || carry != 0; n1--, n2--) {
int c1 = (n1 < 0) ? 0 : (num1.charAt(n1) - '0');
int c2 = (n2 < 0) ? 0 : (num2.charAt(n2) - '0');
sb.append((c1 + c2 + carry) % 10);
carry = (c1 + c2 + carry) / 10;
}
//翻转字符串
return sb.reverse().toString();
}