半平面求交 - 洛谷 - UVA1475 Jungle Outpost

news2024/11/24 2:48:56

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

往期相关背景点击前往

题目大意

题目链接
https://www.luogu.com.cn/problem/UVA1475

在丛林里有n个瞭望塔，瞭望塔的保护范围就是一个凸n多边形，敌人进攻会炸毁一些瞭望塔，使总部暴露在剩下的瞭望塔围成的凸多边形之外，请你选择一个点作为总部，使得敌人要炸毁的瞭望塔尽量多。

解析

此题提到最多要多少个，首先想到枚举+验证的方式。

枚举可以利用二分优化，前提是要证明答案是具体有单调性，既如果炸x个塔不能摧毁防御，那么炸x－1个塔也不能摧毁防御。如果炸x个塔可以摧毁防御，那么炸x+1个塔也可以摧毁防御。

可以先尝试炸1个的情形。
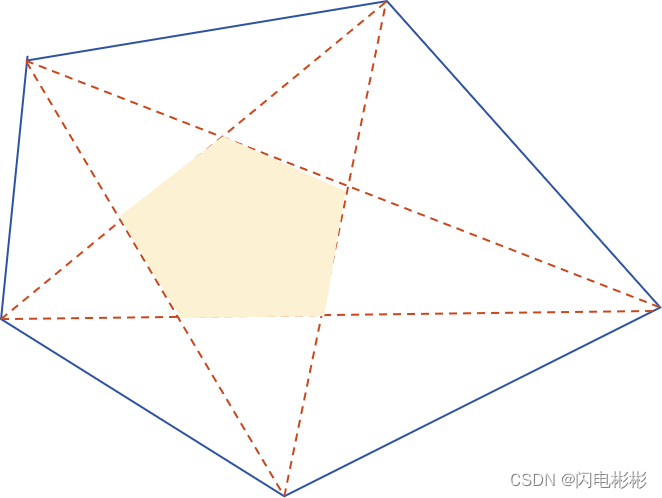
在这里插入图片描述

炸1个那么就是把剩下两个点连边。把所有点都炸1遍，可以看到最后有效防御区域是一个半平面求交凸多边形。上图中表示为黄色区域。

接下来看炸2个的情况。

炸两个有2种策略：

炸连续的两个塔
炸不连续的两个塔

先看炸不连续的情形，

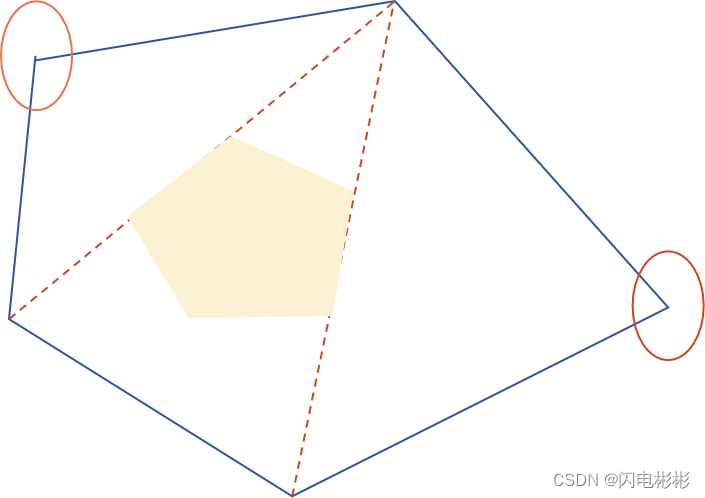
在这里插入图片描述

如果炸不连续的两个塔，则会退化成炸1个塔情形，并不是最优解。从这里可以推断出，这个是一单调的问题。

看炸连续的两个塔，

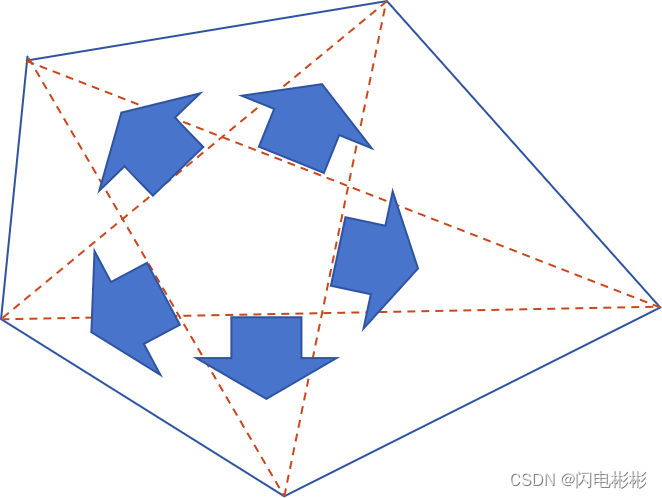
在这里插入图片描述
没有公共区域。

综上所述，如果连续炸掉x个塔，那么答案是关于x单调的。

可以通过二分枚举x, 再构建半平面求交验证的方法解决。

二分枚举点击前往

代码

#include<stdio.h>
#include<cmath>
#include <algorithm>
#include <vector>
#include <list>
#include <cstring>
#include <deque>


using namespace std;
const double EPS = 1e-7;

const int N = 1e5 + 10;

int cmp(double d) {
	if (abs(d) < EPS)return 0;
	if (d > 0)return 1;
	return -1;
}

class Point {
public:
	double x, y;
	int id;

	Point() {}
	Point(double a, double b) :x(a), y(b) {}
	Point(const Point& p) :x(p.x), y(p.y), id(p.id) {}

	void in() {
		scanf("%lf %lf", &x, &y);
	}
	void out() {
		printf("%f %f\n", x, y);
	}

	double dis() {
		return sqrt(x * x + y * y);
	}

	double dis2() {
		return x * x + y * y;
	}

	Point operator -() const {
		return Point(-x, -y);
	}

	Point operator -(const Point& p) const {
		return Point(x - p.x, y - p.y);
	}

	Point operator +(const Point& p) const {
		return Point(x + p.x, y + p.y);
	}
	Point operator *(double d)const {
		return Point(x * d, y * d);
	}

	Point operator /(double d)const {
		return Point(x / d, y / d);
	}


	void operator -=(Point& p) {
		x -= p.x;
		y -= p.y;
	}

	void operator +=(Point& p) {
		x += p.x;
		y += p.y;
	}
	void operator *=(double d) {
		x *= d;
		y *= d;
	}

	void operator /=(double d) {
		this ->operator*= (1 / d);
	}

	bool operator<(const Point& a) const {
		return x < a.x || (abs(x - a.x) < EPS && y < a.y);
	}

	bool operator==(const Point& a) const {
		return abs(x - a.x) < EPS && abs(y - a.y) < EPS;
	}
};

// 向量操作

double cross(const Point& a, const Point& b) {
	return a.x * b.y - a.y * b.x;
}

double dot(const Point& a, const Point& b) {
	return a.x * b.x + a.y * b.y;
}


class Line {
public:
	Point front, tail;
	double ang;
	Line() {}
	Line(const Point& a, const Point& b) :front(a), tail(b) {
		ang = atan2(front.y - tail.y, front.x - tail.x);
	}
};

int cmp(const Line& a, const Line& b) {
	//auto ta = atan2(a.front.y - a.tail.y, a.front.x - a.tail.x);
	//auto tb = atan2(b.front.y - b.tail.y, b.front.x - b.tail.x);

	return cmp(a.ang - b.ang);
}


// 点在直线哪一边>0 左边，<0边
int SideJudge(const Line& a, const Point& b) {
	return cmp(cross(a.front - a.tail, b - a.tail));
}


int LineSort(const Line& a, const Line& b) {
	int c = cmp(a, b);
	if (c)return c < 0;
	return SideJudge(b, a.front) > 0;
}

/*
点p 到 p+r 表示线段1
点q 到 q+s 表示线段2
线段1 上1点用 p' = p+t*r (0<=t<=1)
线段2 上1点用 q' = q+u*s (0<=u<=1)
让两式相等求交点 p+t*r = q+u*s
两边都叉乘s
(p+t*r)Xs = (q+u*s)Xs
pXs + t*rXs = qXs
t = (q-p)Xs/(rXs)
同理，
u = (p-q)Xr/(sXr) -> u = (q-p)Xr/(rXs)

以下分4种情况：
1. 共线，sXr==0 && (q-p)Xr==0, 计算 (q-p)在r上的投影在r长度上的占比t0，
计算(q+s-p)在r上的投影在r长度上的占比t1，查看[t0, t1]是否与范围[0，1]有交集。
如果t0>t1, 则比较[t1, t0]是否与范围[0，1]有交集。
t0 = (q-p)*r/(r*r)
t1 = (q+s-p)*r/(r*r) = t0 + s · r / (r · r)
2. 平行sXr==0 && (q-p)Xr!=0
3. 0<=u<=1 && 0<=t<=1 有交点
4. 其他u, t不在0到范围内，没有交点。
*/
pair<double, double> intersection(const Point& q, const Point& s, const Point& p, const Point& r) {
	// 计算 (q-p)Xr
	auto qpr = cross(q - p, r);
	auto qps = cross(q - p, s);

	auto rXs = cross(r, s);
	if (cmp(rXs) == 0)return { -1, -1 }; // 平行或共线
	// 求解t, u
	// t = (q-p)Xs/(rXs)
	auto t = qps / rXs;

	// u = (q-p)Xr/(rXs)
	auto u = qpr / rXs;

	return { u, t };
}

Point LineCross(const Line& a, const Line& b) {
	Point dira = a.front - a.tail;
	Point dirb = b.front - b.tail;

	auto p = intersection(a.tail, dira, b.tail, dirb);
	return a.tail + dira * p.first;
}

class HalfPlane {
public:
	vector<Line> lines;
	vector<int> q;
	vector<Point> t;
	int len;

	HalfPlane() {
		lines.resize(N);
		q.resize(N);
		t.resize(N);
	}

	void addLine(const Line& a) {
		lines[len++]=a;
	}

	vector<Point> run() {
		sort(lines.begin(), lines.begin()+len, LineSort);

		int l = -1, r = 0;
		q[0] = 0;
		for (int i = 1; i < len; ++i) {
			if (cmp(lines[i], lines[i - 1]) == 0)continue;
			while (r - l > 1 && SideJudge(lines[i], t[r]) < 0)r--;
			while (r - l > 1 && SideJudge(lines[i], t[l + 2]) < 0)l++;
			q[++r] = i;
			t[r] = LineCross(lines[q[r]], lines[q[r - 1]]);
		}
		while (r - l > 1 && SideJudge(lines[q[l + 1]], t[r]) < 0)r--;
		t[r + 1] = LineCross(lines[q[l + 1]], lines[q[r]]);
		r++;

		// 统计交点
		l++;
		vector<Point> ans(r - l);
		for (int i = 0; i < ans.size(); ++i) {
			ans[i] = t[i + l + 1];
		}

		return ans;
	}
};

Point oiPs[N*2];
HalfPlane hp;

bool boomJudge(int n, int k) {
	hp.len = 0;
	for (int i = 0; i < n; ++i) {
		hp.addLine(Line(oiPs[i+k+1], oiPs[i]));
	}

	auto keyPoints = hp.run();
	double ans = 0;
	for (int i = 2; i < keyPoints.size(); ++i) {
		ans += cross(keyPoints[i - 1] - keyPoints[0], keyPoints[i] - keyPoints[0]);
	}

	return cmp(ans/2) == 0;
}

void  solve() {
	int n;
	
	while (scanf("%d", &n) ==1 &&n) {
		int a, b;

		for (int i = n - 1; i >= 0; --i) {
			scanf("%d%d", &a, &b);
			oiPs[i] = Point(a, b);
			oiPs[i + n] = oiPs[i];
		}

		int l = 1, r = n-2;

		while (l < r) {
			int mid = (l + r) >> 1;
			if (boomJudge(n, mid)) {
				r = mid;
			}
			else {
				l = mid + 1;
			}
		}

		printf("%d\n", l);
	}
}


int main() {
	solve();
	return 0;

}

/*
3
0 0
50 50
60 10
5
0 0
0 10
10 20
20 10
25 0

*/