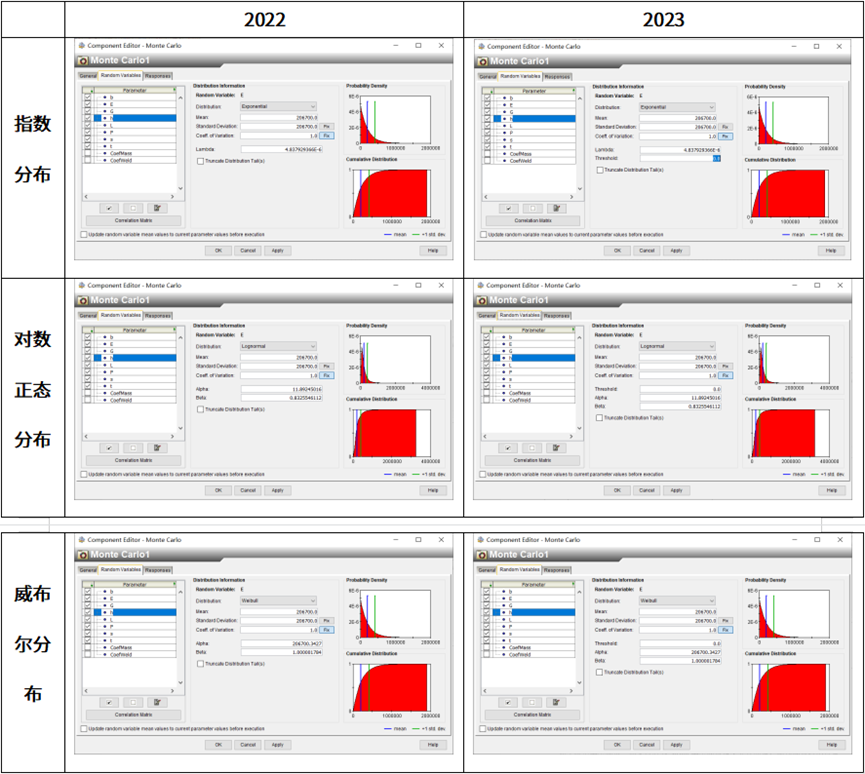
DMA隐蔽通信的新思路

拆分DMA的RF链

思路的主要来源:
@article{Ci2021HybridBD,
title={Hybrid Beamforming Design for Covert Multicast mmWave Massive MIMO Communications},
author={Wei Ci and Chenhao Qi and Geoffrey Ye Li and Shiwen Mao},
journal={2021 IEEE Global Communications Conference (GLOBECOM)},
year={2021},
volume={},
pages={}
}

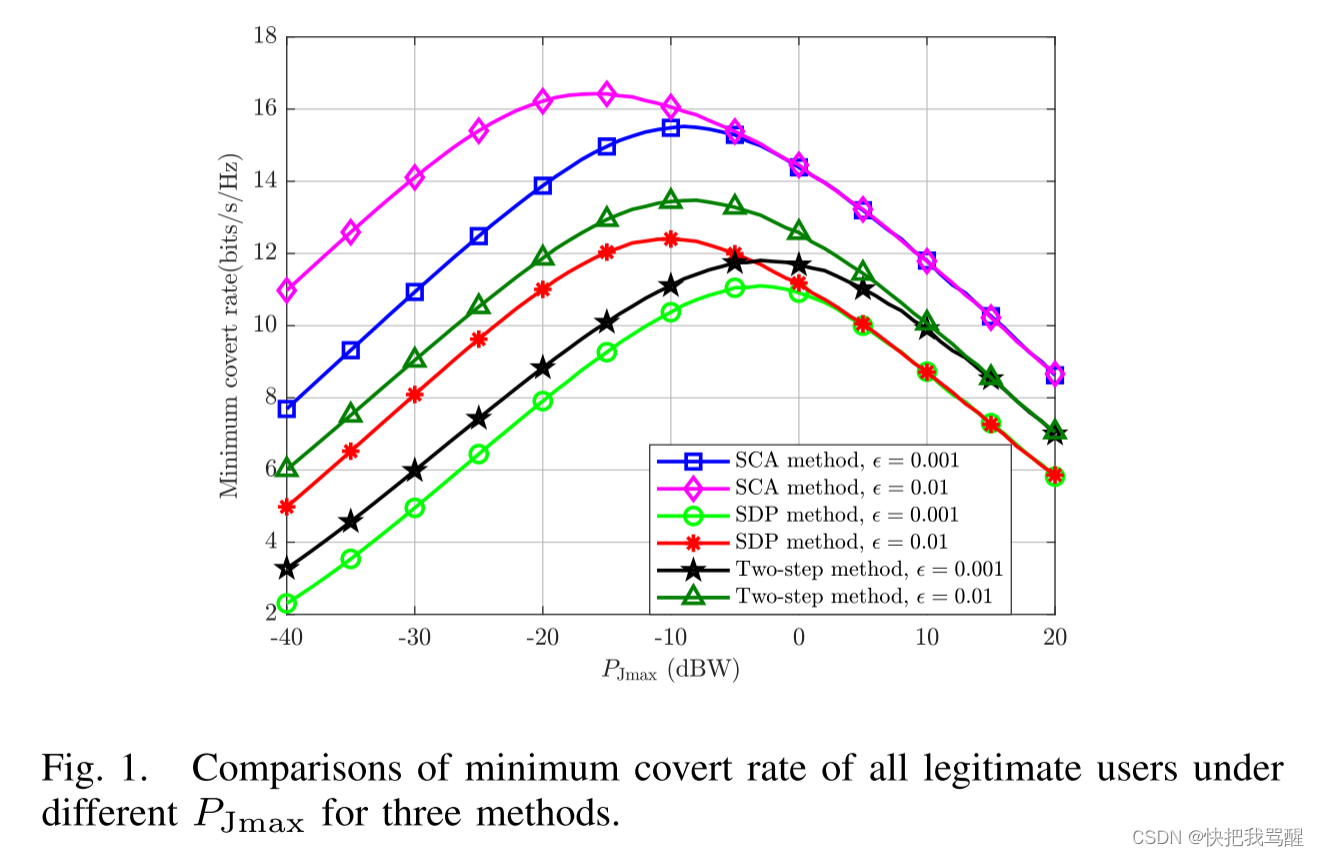
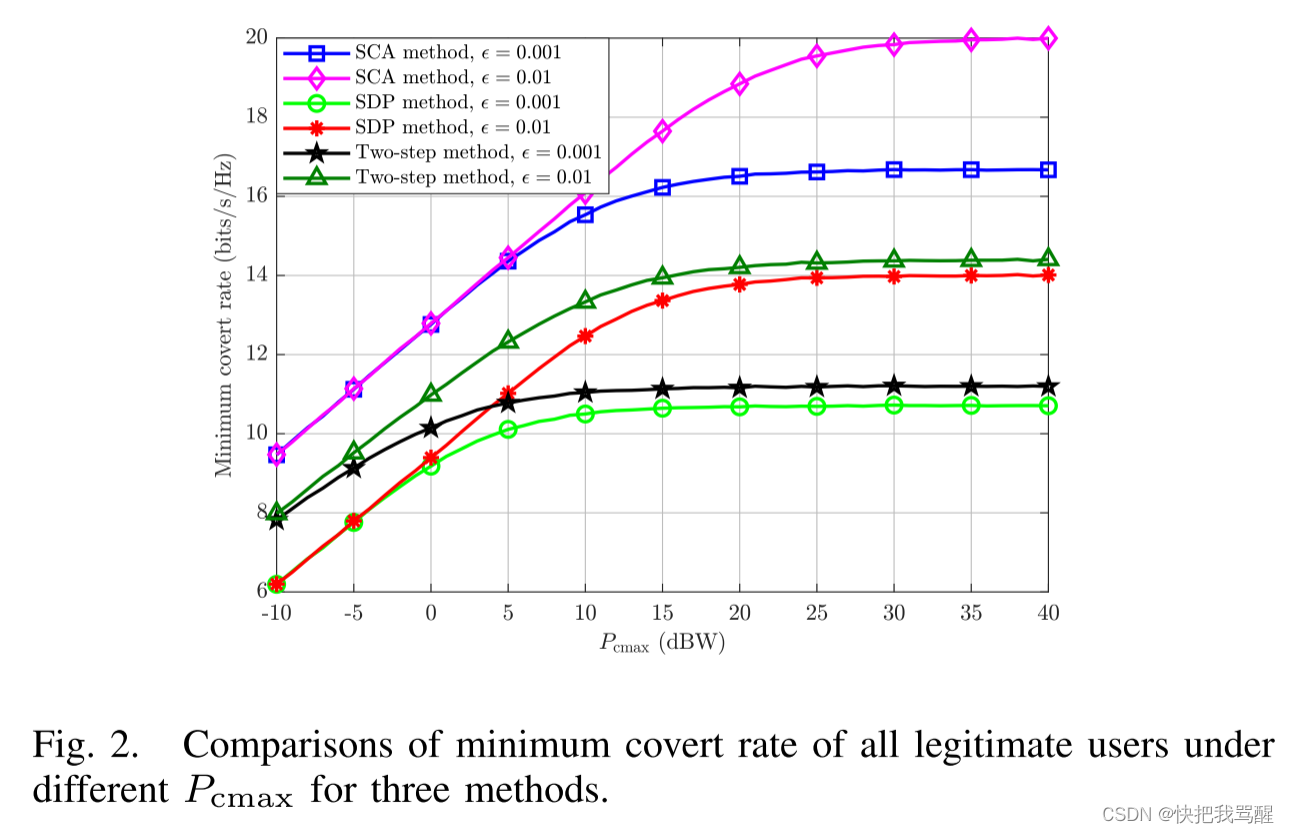
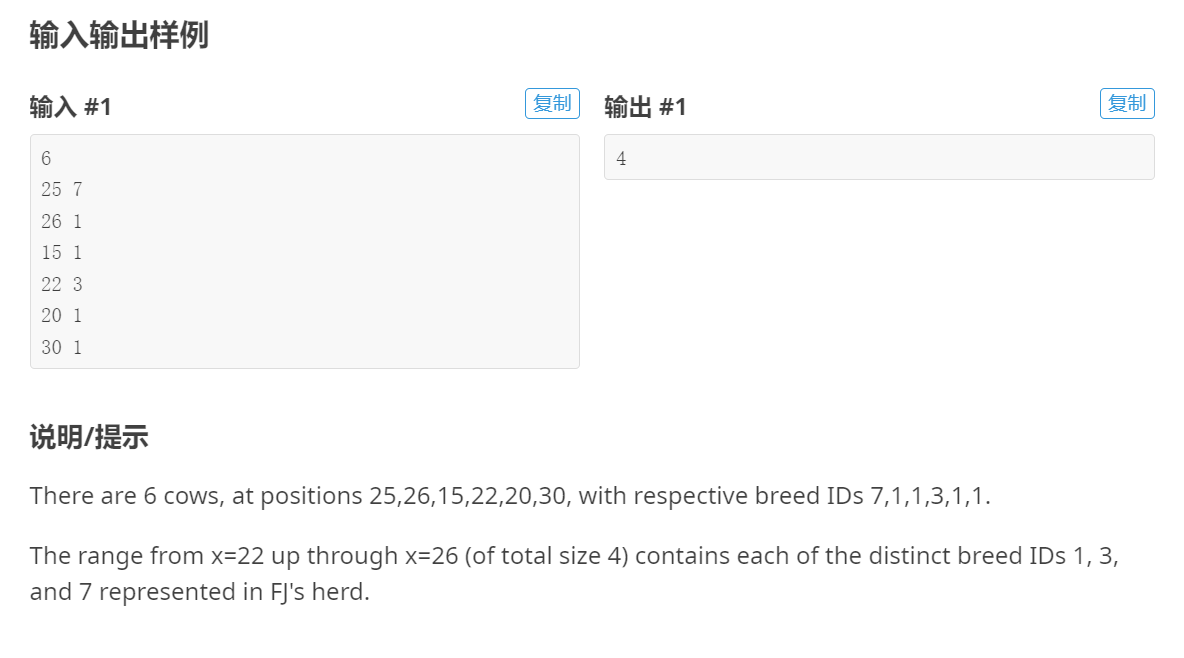
文章的仿真图,注意这篇文章是多用户的,纵轴是最小隐蔽速率, 横轴是最大干扰功率和PcMAX是?
Multiuser Covert Communication 多合法用户隐蔽通信?
思考: DMA可以用于远场吗?DMA用于远场的模型

下一步是首先看看多用户的隐蔽,然后看看能不能把这个文章复现出来.

$$\begin{array}{r}r\left({\mathbf{p}}_i\right)={\mathbf{a}}_i^H\mathbf{s}+n_i,i=b\text{ or }w\end{array}$$

The digital input to the DMA is given by $\mathbf{w}={\left[\sqrt{P_c}{\mathbf{w}}_b^T{x}_b,\sqrt{P_J}{\mathbf{w}}_w^T{x}_w\right]}^T$ , and thus by (1) the channel input is

$$\mathbf{s}=\mathbf{HQ}\mathbf{w}$$

$$\begin{array}{r}r\left({\mathbf{p}}_i\right)={\mathbf{a}}_i^H\mathbf{HQ}\mathbf{w}+n_i,i=b\text{ or }w\end{array}$$

$\mathbf{H}\in {\mathbb{C}}^{N_d{N}_e\times N_d{N}_e}$
${\mathbf{H}}_b\in {\mathbb{C}}^{N_{dc}{N}_e\times N_{dc}{N}_e}$
${\mathbf{H}}_w\in {\mathbb{C}}^{N_{dj}{N}_e\times N_{dj}{N}_e}$

$\mathbf{Q}\in {\mathbb{C}}^{N_d{N}_e\times N_d}$ 不涉及发射功率分量
${\mathbf{Q}}_b\in {\mathbb{C}}^{N_{dc}{N}_e\times N_{dc}}$
${\mathbf{Q}}_w\in {\mathbb{C}}^{N_{dj}{N}_e\times N_{dj}}$

${\mathbf{w}}_b\in {\mathbb{C}}^{N_d\times 1}$
$||{\mathbf{w}}_b|{|}_2^2=1$
${\mathbf{w}}_w\in {\mathbb{C}}^{N_d\times 1}$
$||{\mathbf{w}}_w|{|}_2^2=1$

$P_w$ is the power of the jamming signal $e_w$ , which obeys the uniform distribution in
$P_w\sim \left[0,P_{wmax}\right]$

$P_b\le P_{bmax}$
where $b$ and $w$ denote Bob and Willie, respectively, $n_i\sim \mathcal{N}\left(0,{\sigma }_i^2\right)$ denote the noise at Bob or Willie.

有人工噪声

${\mathcal{H}}_0:r\left({\mathbf{p}}_w\right)=\sqrt{P_w}{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w+n_w$

${\mathcal{H}}_1:r\left({\mathbf{p}}_w\right)=\sqrt{P_b}{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b+\sqrt{P_w}{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w+n_w$

Willie有足够的时间来积累能量

${\mathcal{H}}_0:T_0=|r\left({\mathbf{p}}_w\right){|}^2=P_w{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2+{\sigma }_w^2$

${\mathcal{H}}_1:T_1=|r\left({\mathbf{p}}_w\right){|}^2=P_b{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2+P_w{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2+{\sigma }_w^2$

无人工噪声

${\mathcal{H}}_0:r\left({\mathbf{p}}_w\right)=n_w$

${\mathcal{H}}_1:r\left({\mathbf{p}}_w\right)={\mathbf{a}}_i^H\mathbf{HQ}({\mathbf{w}}_b{e}_b)+n_w$

Optimal detection threshold: $\tau$

Willie makes a binary decision on whether the received signal is noise or signal plus noise.

The test statistic is given by : $T\left({\mathbf{y}}_w\right)=|r\left({\mathbf{p}}_w\right){|}^2$

Denote $D_0$ and $D_1$ as the decisions that the received signal is noise and that the received signal is signal plus noise, respectively.

$P_{\mathrm{FA}}=\mathbb{P}\left(D_1\mid {\mathcal{H}}_0\right)=Pr(T_0\ge \tau )$
$P_{\mathrm{MD}}=\mathbb{P}\left(D_0\mid {\mathcal{H}}_1\right)=Pr(T_1<\tau )$

$${\mathcal{P}}_{\mathrm{FA}}=\mathrm{Pr}\left(T_0\ge \tau \right)=\{\begin{array}{ll}1,& \tau <{\sigma }_{\mathrm{w}}^2\\ 1-\frac{\tau -{\sigma }_{\mathrm{w}}^2}{P_{\mathrm{w}\max }{|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w|}^2},& {\sigma }_{\mathrm{w}}^2\le \tau <{\sigma }_{\mathrm{w}}^2+P_{\mathrm{w}\max }{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2\\ 0,& \tau \ge {\sigma }_{\mathrm{w}}^2+P_{\mathrm{w}\max }{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2\end{array}$$

$${\mathcal{P}}_{\mathrm{MD}}=\mathrm{Pr}\left(T_1<\tau \right)=\{\begin{array}{ll}0,& \tau <{\sigma }_{\mathrm{w}}^2+P_{\mathrm{b}}{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2\\ \frac{\tau -{\sigma }_{\mathrm{w}}^2-P_{\mathrm{b}}{|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b|}^2}{P_{\mathrm{w}\max }{|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w|}^2},& {\sigma }_{\mathrm{w}}^2+P_{\mathrm{b}}{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2\le \tau <{\sigma }_{\mathrm{w}}^2+P_{\mathrm{b}}{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2+P_{\mathrm{w}\max }{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2\\ 1,& \tau \ge {\sigma }_{\mathrm{w}}^2+P_{\mathrm{b}}{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2+P_{\mathrm{w}\max }{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2\end{array}$$

In the worst case, Willie has a perfect knowledge of the channel from Alice to Willie:

$${\mathcal{P}}_{\mathrm{e}}\triangleq {\mathcal{P}}_{\mathrm{FA}}+{\mathcal{P}}_{\mathrm{MD}}$$

if ${\mathcal{P}}_{\mathrm{e}}=0$, due to the expression of ${\mathcal{P}}_{\mathrm{FA}}=0$ and ${\mathcal{P}}_{\mathrm{MD}}=0$ :

$P_{w\max }{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2\le P_b{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2$

So we can’t make $P_{w\max }{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2\le P_b{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2$ hold

To ensure ${\mathcal{P}}_{\mathrm{e}}\ne 0$: We should make:

$P_{w\max }{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2>P_b{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2$

$${\mathcal{P}}_{\mathrm{e}}=\{\begin{array}{ll}1-\frac{\tau -{\sigma }_{\mathrm{w}}^2}{P_{w\max }{|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w|}^2},& {\sigma }_{\mathrm{w}}^2\le \tau <{\sigma }_{\mathrm{w}}^2+P_b{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2\\ 1-\frac{P_b{|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b|}^2}{P_{w\max }{|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w|}^2},& {\sigma }_{\mathrm{w}}^2+P_b{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2\le \tau <{\sigma }_{\mathrm{w}}^2+P_{w\max }{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2\\ \frac{\tau -{\sigma }_{\mathrm{w}}^2-P_b{|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b|}^2}{P_{w\max }{|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w|}^2},& {\sigma }_{\mathrm{w}}^2+P_{w\max }{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2\le \tau <{\sigma }_{\mathrm{w}}^2+P_b{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2+P_{w\max }{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2\\ 1,& \text{ else }\end{array}\text{\hspace{1em}(21)}$$

对${\mathcal{P}}_{\mathrm{e}}$求导，然后可以发现：

Optimal $\tau$ achieved by (21b)

$${\hat{\mathcal{P}}}_{\mathrm{e}}=1-\frac{P_b{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2}{P_{w\max }{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2},$$

SINR at Bob
$${\gamma }_b\triangleq \frac{P_b{\left|{\mathbf{a}}_b^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2}{P_w{\left|{\mathbf{a}}_b^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2+{\sigma }_b^2}\text{\hspace{1em}(23)}$$

We need to maximize ${\gamma }_b$

The covert rate :

$$R_b={\log }_2\left(1+{\gamma }_b\right)$$

maximize the covert rate:
Optimization problem about ${\mathbf{w}}_w$,${\mathbf{w}}_b$,$\mathbf{Q}$, $P_b$

$$\begin{array}{rl}\underset{{\mathbf{w}}_w,{\mathbf{w}}_b,\mathbf{Q},P_b}{\max }& R_b,\\ \text{ s.t. }& {\hat{\mathcal{P}}}_{\mathrm{e}}\ge 1-ϵ,\\ & P_b\le P_{bmax},\\ & ||{\mathbf{w}}_b|{|}_2^2=1,\\ & ||{\mathbf{w}}_w|{|}_2^2=1,\\ & \mathbf{Q}的约束\end{array}\text{\hspace{1em}(24)}$$

---

(Constraint 1 is equal to)

$$P_{\mathrm{b}}\le g\left({\mathbf{w}}_{\mathrm{b}},{\mathbf{w}}_{\mathrm{w}},\mathbf{Q}\right)\text{\hspace{1em}(25)}$$

$g\left({\mathbf{w}}_{\mathrm{b}},{\mathbf{w}}_{\mathrm{w}},\mathbf{Q}\right)$ is expressed as:

$$g\left({\mathbf{w}}_{\mathrm{b}},{\mathbf{w}}_{\mathrm{w}},\mathbf{Q}\right)\triangleq \frac{ϵP_{w\max }{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2}{{\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2}\text{\hspace{1em}(26)}$$

Note that (23) monotonically increases with $P_b$.

The optimal $P_b$:

P ~ b = min ⁡ { P b m a x , g ( w b , w w , Q ) } . (27) \widetilde{P}_{\mathrm{b}}=\min \left\{P_{\mathrm{bmax}}, g\left( \mathbf{w}_{\mathrm{b}}, \mathbf{w}_{\mathrm{w}}, \mathbf{Q} \right) \right\} . \tag{27} P b​=min{Pbmax​,g(wb​,ww​,Q)}.(27)

---

(25) (26) (27) 联合表述了第一个约束和第二个约束

---

针对$P_b$问题的优化：

---

$$\underset{{\mathbf{w}}_{\mathrm{b}},{\mathbf{w}}_{\mathrm{w}},\mathbf{Q}}{\max }g\left({\mathbf{w}}_{\mathrm{b}},{\mathbf{w}}_{\mathrm{w}},\mathbf{Q}\right).\text{\hspace{1em}(28)}$$

---

主目标函数，最大化Bob处的信噪比

---

Due to (23), we need to maximize ${\left|{\mathbf{a}}_b^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2$ and minimize ${\left|{\mathbf{a}}_b^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2$

Hopefully there are feasible solutions for

$${\mathbf{a}}_b^H\mathbf{HQ}{\mathbf{w}}_w{e}_w=0\text{\hspace{1em}(29)}$$

---

Then the optimization of ${\mathbf{w}}_w$ and ${\mathbf{w}}_b$ is decoupled. (24) is converted into the following two independent optimization problems as

$$\begin{array}{rl}\underset{{\mathbf{w}}_{\mathrm{w}}}{\max }& {\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_w{e}_w\right|}^2\\ \text{ s.t. }& {\Vert {\mathbf{w}}_{\mathrm{w}}\Vert }_2^2=1,\\ & {\mathbf{a}}_b^H\mathbf{HQ}{\mathbf{w}}_w{e}_w=0,\end{array}\text{\hspace{1em}(30)}$$

$$\begin{array}{rl}\underset{{\mathbf{w}}_{\mathrm{b}}}{\max }& \frac{{\left|{\mathbf{a}}_b^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2}{{\sigma }_b^2}\\ \text{ s.t. }& {\left|{\mathbf{a}}_w^H\mathbf{HQ}{\mathbf{w}}_b{e}_b\right|}^2=0,\\ & {\Vert {\mathbf{w}}_{\mathrm{b}}\Vert }_2^2=1\end{array}\text{\hspace{1em}(31)}$$

where (30a) and (31b) are based on (28) and the transformation from (24a) to (31a) is based on (29).

---