【数据结构】树与二叉树（十八）：树的存储结构——Father链接结构、儿子链表链接结构

news2024/11/24 5:44:03

文章目录

  • 5.1 树的基本概念
    • 5.1.1 树的定义
    • 5.1.2 森林的定义
    • 5.1.3 树的术语
  • 5.2 二叉树
  • 5.3 树
    • 5.3.1 树的存储结构
      • 1. 理论基础
      • 2. 典型实例
    • 5.3.2 Father链接结构
      • a. 定义树节点结构
      • b. 创建新节点
      • c. 主函数
      • d. 代码整合
    • 5.3.3 儿子链表链接结构
      • a. 定义树节点结构
      • b. 创建新节点
      • c. 添加子节点作为第一个子节点
      • d. 遍历树打印节点数据
      • e. 主函数
      • f. 代码整合

5.1 树的基本概念

5.1.1 树的定义

  • 一棵树是结点的有限集合T：
    • 若T非空，则：
      • 有一个特别标出的结点，称作该树的根，记为root(T)；
      • 其余结点分成若干个不相交的非空集合T1, T2, …, Tm (m>0)，其中T1, T2, …, Tm又都是树，称作root(T)的子树。
    • T 空时为空树，记作root(T)=NULL。

5.1.2 森林的定义

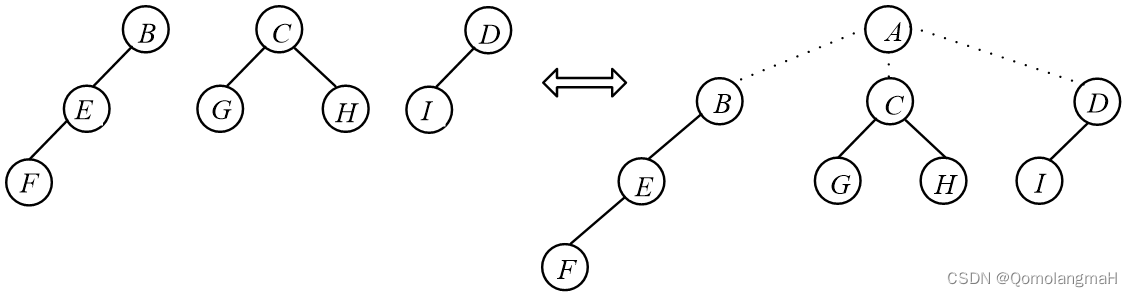
  一个森林是0棵或多棵不相交（非空）树的集合，通常是一个有序的集合。换句话说，森林由多个树组成，这些树之间没有交集，且可以按照一定的次序排列。在森林中，每棵树都是独立的，具有根节点和子树，树与树之间没有直接的连接关系。
  森林是树的扩展概念，它是由多个树组成的集合。在计算机科学中，森林也被广泛应用于数据结构和算法设计中，特别是在图论和网络分析等领域。
在这里插入图片描述

5.1.3 树的术语

  • 父亲（parent）、儿子（child）、兄弟（sibling）、后裔（descendant）、祖先（ancestor）
  • 度（degree）、叶子节点（leaf node）、分支节点（internal node）
  • 结点的层数
  • 路径、路径长度、结点的深度、树的深度

参照前文：【数据结构】树与二叉树（一）：树（森林）的基本概念：父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度

5.2 二叉树

5.3 树

5.3.1 树的存储结构

1. 理论基础

  1. Father链接结构:

    • 在这种结构中，每个节点除了存储数据外，还包含一个指向其父节点的指针。
    • 这种结构使得查找父节点很容易，但对于查找子节点则较为困难，因为需要遍历整个树。
    • 在二叉树中，每个节点最多有一个父节点，但在一般的树中，节点可以有多个父节点。

  2. 儿子链表链接结构:

    • 在这种结构中，每个节点包含一个指向其第一个子节点的指针，以及一个指向其下一个兄弟节点的指针。
    • 这种结构使得查找子节点很容易，但查找父节点较为困难，可能需要遍历兄弟节点链表直到找到相应的父节点。

  3. 左儿子右兄弟链接结构:

    • 也称为孩子兄弟表示法，每个节点包含一个指向其第一个子节点的指针，以及一个指向其下一个兄弟节点的指针。
    • 在这种结构中，树的每一层被表示为一个单链表，子节点通过左链连接，兄弟节点通过右链连接。
    • 这种结构既方便查找父节点，又方便查找子节点和兄弟节点，被广泛用于一般的树的表示。

  选择合适的树的存储结构通常取决于具体应用的需求。 Father链接结构适合于查找父节点的操作频繁，而儿子链表链接结构和左儿子右兄弟链接结构适用于频繁查找子节点的情况。

2. 典型实例

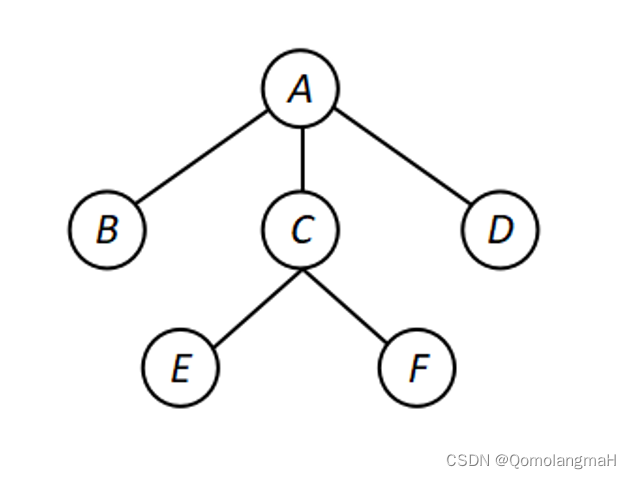
在这里插入图片描述

  1. Father链接结构:
    • A节点：父指针为null（A为根节点）
    • B节点：父指针指向A
    • C节点：父指针指向A
    • D节点：父指针指向A
    • E节点：父指针指向C
    • F节点：父指针指向C
  2. 儿子链表链接结构:
    • A节点：子节点链表为B、C、D
    • B节点：子节点链表为null
    • C节点：子节点链表为E、F
    • D节点：子节点链表为null
    • E节点：子节点链表为null
    • F节点：子节点链表为null
  3. 左儿子右兄弟链接结构:
    • A节点：左儿子为B，右兄弟为null
    • B节点：左儿子为null，右兄弟为C
    • C节点：左儿子为E，右兄弟为D
    • D节点：左儿子为null，右兄弟为null
    • E节点：左儿子为null，右兄弟为F
    • F节点：左儿子为null，右兄弟为null

5.3.2 Father链接结构

a. 定义树节点结构

typedef struct TreeNode {
    char data;              // 节点数据
    struct TreeNode* parent; // 指向父节点的指针
} TreeNode;

b. 创建新节点

TreeNode* createNode(char data) {
    TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));
    if (newNode == NULL) {
        fprintf(stderr, "Memory allocation failed\n");
        exit(EXIT_FAILURE);
    }
    newNode->data = data;
    newNode->parent = NULL;
    return newNode;
}

c. 主函数

int main() {
    // 创建节点
    TreeNode* nodeA = createNode('A');
    TreeNode* nodeB = createNode('B');
    TreeNode* nodeC = createNode('C');
    TreeNode* nodeD = createNode('D');
    TreeNode* nodeE = createNode('E');
    TreeNode* nodeF = createNode('F');

    // 构建树结构，设置父指针
    nodeB->parent = nodeA;
    nodeC->parent = nodeA;
    nodeD->parent = nodeA;
    nodeE->parent = nodeC;
    nodeF->parent = nodeC;

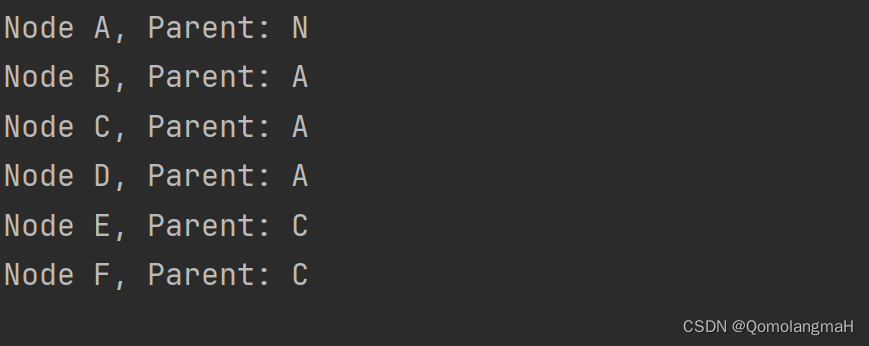
    // 打印每个节点及其父节点
    printf("Node %c, Parent: %c\n", nodeA->data, (nodeA->parent ? nodeA->parent->data : 'N'));
    printf("Node %c, Parent: %c\n", nodeB->data, (nodeB->parent ? nodeB->parent->data : 'N'));
    printf("Node %c, Parent: %c\n", nodeC->data, (nodeC->parent ? nodeC->parent->data : 'N'));
    printf("Node %c, Parent: %c\n", nodeD->data, (nodeD->parent ? nodeD->parent->data : 'N'));
    printf("Node %c, Parent: %c\n", nodeE->data, (nodeE->parent ? nodeE->parent->data : 'N'));
    printf("Node %c, Parent: %c\n", nodeF->data, (nodeF->parent ? nodeF->parent->data : 'N'));

    // 释放内存
    free(nodeA);
    free(nodeB);
    free(nodeC);
    free(nodeD);
    free(nodeE);
    free(nodeF);

    return 0;
}

d. 代码整合

#include <stdio.h>
#include <stdlib.h>

// 定义树节点结构
typedef struct TreeNode {
    char data;              // 节点数据
    struct TreeNode* parent; // 指向父节点的指针
} TreeNode;

// 创建新节点的函数
TreeNode* createNode(char data) {
    TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));
    if (newNode == NULL) {
        fprintf(stderr, "Memory allocation failed\n");
        exit(EXIT_FAILURE);
    }
    newNode->data = data;
    newNode->parent = NULL;
    return newNode;
}

int main() {
    // 创建节点
    TreeNode* nodeA = createNode('A');
    TreeNode* nodeB = createNode('B');
    TreeNode* nodeC = createNode('C');
    TreeNode* nodeD = createNode('D');
    TreeNode* nodeE = createNode('E');
    TreeNode* nodeF = createNode('F');

    // 构建树结构，设置父指针
    nodeB->parent = nodeA;
    nodeC->parent = nodeA;
    nodeD->parent = nodeA;
    nodeE->parent = nodeC;
    nodeF->parent = nodeC;

    // 打印每个节点及其父节点
    printf("Node %c, Parent: %c\n", nodeA->data, (nodeA->parent ? nodeA->parent->data : 'N'));
    printf("Node %c, Parent: %c\n", nodeB->data, (nodeB->parent ? nodeB->parent->data : 'N'));
    printf("Node %c, Parent: %c\n", nodeC->data, (nodeC->parent ? nodeC->parent->data : 'N'));
    printf("Node %c, Parent: %c\n", nodeD->data, (nodeD->parent ? nodeD->parent->data : 'N'));
    printf("Node %c, Parent: %c\n", nodeE->data, (nodeE->parent ? nodeE->parent->data : 'N'));
    printf("Node %c, Parent: %c\n", nodeF->data, (nodeF->parent ? nodeF->parent->data : 'N'));

    // 释放内存
    free(nodeA);
    free(nodeB);
    free(nodeC);
    free(nodeD);
    free(nodeE);
    free(nodeF);

    return 0;
}

在这里插入图片描述

注：其他操作……有缘再见

5.3.3 儿子链表链接结构

a. 定义树节点结构

struct TreeNode {
    char data;
    struct TreeNode* child;
    struct TreeNode* sibling;
};

b. 创建新节点

struct TreeNode* createNode(char data) {
    struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    newNode->data = data;
    newNode->child = NULL;
    newNode->sibling = NULL;
    return newNode;
}

c. 添加子节点作为第一个子节点

void addChild(struct TreeNode* parent, struct TreeNode* child) {
    child->sibling = parent->child;
    parent->child = child;
}

d. 遍历树打印节点数据


void traverseTree(struct TreeNode* root) {
    if (root != NULL) {
        printf("%c\n", root->data);

        struct TreeNode* child = root->child;
        while (child != NULL) {
            printf("  %c (Child)\n", child->data);
            child = child->sibling;
        }

        // 递归遍历每个子节点
        child = root->child;
        while (child != NULL) {
            traverseTree(child);
            child = child->sibling;
        }
    }
}

e. 主函数

int main() {
    // 创建树节点
    struct TreeNode* A = createNode('A');
    struct TreeNode* B = createNode('B');
    struct TreeNode* C = createNode('C');
    struct TreeNode* D = createNode('D');
    struct TreeNode* E = createNode('E');
    struct TreeNode* F = createNode('F');

    // 构建树结构
    addChild(A, B);
    addChild(A, C);
    addChild(A, D);
    addChild(C, E);
    addChild(C, F);

    // 遍历并打印树节点
    traverseTree(A);

    // 释放内存
    free(A);
    free(B);
    free(C);
    free(D);
    free(E);
    free(F);

    return 0;
}

在这里插入图片描述

f. 代码整合

#include <stdio.h>
#include <stdlib.h>

// 定义树节点结构
struct TreeNode {
    char data;
    struct TreeNode* child;
    struct TreeNode* sibling;
};

// 创建新节点
struct TreeNode* createNode(char data) {
    struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    newNode->data = data;
    newNode->child = NULL;
    newNode->sibling = NULL;
    return newNode;
}

// 添加子节点作为第一个子节点
void addChild(struct TreeNode* parent, struct TreeNode* child) {
    child->sibling = parent->child;
    parent->child = child;
}

// 遍历树并打印节点
void traverseTree(struct TreeNode* root) {
    if (root != NULL) {
        printf("%c\n", root->data);

        struct TreeNode* child = root->child;
        while (child != NULL) {
            printf("  %c (Child)\n", child->data);
            child = child->sibling;
        }

        // 递归遍历每个子节点
        child = root->child;
        while (child != NULL) {
            traverseTree(child);
            child = child->sibling;
        }
    }
}

int main() {
    // 创建树节点
    struct TreeNode* A = createNode('A');
    struct TreeNode* B = createNode('B');
    struct TreeNode* C = createNode('C');
    struct TreeNode* D = createNode('D');
    struct TreeNode* E = createNode('E');
    struct TreeNode* F = createNode('F');

    // 构建树结构
    addChild(A, B);
    addChild(A, C);
    addChild(A, D);
    addChild(C, E);
    addChild(C, F);

    // 遍历并打印树节点
    traverseTree(A);

    // 释放内存
    free(A);
    free(B);
    free(C);
    free(D);
    free(E);
    free(F);

    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1220232.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

DOORS和Reqtify—需求管理和需求追溯工具

DOORS和Reqtify—需求管理和需求追溯工具

产品概述 IBM Rational DOORS可实现对整个产品的全生命周期需求管理&#xff0c;覆盖从需求、到设计以及测试阶段&#xff0c;是一款被广泛使用的企业级专业需求管理工具。DOORS可以将项目开发过程中产生的各级需求和与需求相关的文件、网址URL进行链接管理&#xff0c;同时能够…
阅读更多...
微信小程序Error: ENOENT: no such file

微信小程序Error: ENOENT: no such file

问题描述 当编译的时候 会提示找不到这个文件&#xff08;index&#xff09;&#xff0c;但是确信项目目录里已经删除了该页面路径&#xff0c;并且app.json的pages列表中也 导致这个问题应该是&#xff1a;新添加了文件&#xff0c;后面删除了或者修改了文件名&#xff0c;导…
阅读更多...
Vue3.0和2.0语法不同分析

Vue3.0和2.0语法不同分析

前言&#xff1a;本篇文章只做VUE3.0和VUE2.0语法上的不同分析&#xff0c;不做性能和源码架构等的分析。 一、VUE3.0和VUE2.0代码结构不同 VUE3.0代码实例 <template><div><span>count is {{ count }}</span><span>plusOne is {{ plusOne }}…
阅读更多...
AH8691-60V降压至3.3V电源芯片：ESOP8封装解决方案

AH8691-60V降压至3.3V电源芯片：ESOP8封装解决方案

AH8691-60V降压至3.3V电源芯片&#xff1a;ESOP8封装解决方案 随着电子设备的日益普及&#xff0c;电源管理芯片的重要性也日益凸显。一款高效率、低功耗的电源芯片可以大大提高电子设备的性能和可靠性。今天&#xff0c;我们将介绍一款60V降压至3.3V电源芯片&#xff0c;采用…
阅读更多...
c++递归分析出依赖的头文件

c++递归分析出依赖的头文件

我想使用boost::optional&#xff0c;但boost库太大&#xff0c;添加到git时比较费劲。 怎样分析出boost/optional.hpp依赖的头文件&#xff0c;然后精准地添加到git上呢&#xff1f; 使用g就可以了&#xff0c;步骤如下 进入目录boost_1_78_0/boost执行 g -MM -H optional.hp…
阅读更多...
04-快速掌握Redis,了解Redis中常见的结构类型及其应用场景

04-快速掌握Redis,了解Redis中常见的结构类型及其应用场景

Redis快速入门 Remote Dctionary Server Redis是用C语言开发的一个开源的、基于内存的(高性能)键值对(key-value)结构化NoSql数据库,每秒内查询次数可以达到100000的QPS 键值型: Redis中存储的数据都是以key、value对的形式存储&#xff0c;而value的形式多种多样(如字符串、…
阅读更多...
低代码，让我效率提升了80%

低代码，让我效率提升了80%

目录 ​编辑 一、前言 二、优势 三、主要功能点 四、低代码归根结底差不多 五、小结 一、前言 低代码开发平台&#xff0c;一个号称能在几分钟的时间里开发出一套公司内部都可使用的应用系统开发工具。很多人或许都隐隐听说过低代码&#xff0c;因为低代码不仅远名国外&#xf…
阅读更多...
003 OpenCV filter2D

003 OpenCV filter2D

目录 一、环境 二、图像卷积 三、代码演示 3.1、锐化 3.2、sobel边缘&#xff0c;x方向 3.3、sobel边缘&#xff0c;y方向 3.4、高斯模糊 3.5、完整代码 一、环境 本文使用环境为&#xff1a; Windows10Python 3.9.17opencv-python 4.8.0.74 二、图像卷积 在OpenCV…
阅读更多...
CentOS停服背景下“浪潮信息KeyarchOS(KOS)系统迁移(无缝切换)解决方案”

CentOS停服背景下“浪潮信息KeyarchOS(KOS)系统迁移(无缝切换)解决方案”

1 前言 1.1 背景介绍 CentOS停服事件源于2020年12月宣布的CentOS项目变更&#xff0c;其原计划是基于Red Hat Enterprise Linux&#xff08;RHEL&#xff09;的开源版本&#xff0c;提供长期支持。然而&#xff0c;在2020年12月8日&#xff0c;官方宣布终止CentOS Linux的项目…
阅读更多...
【数学】正投影和仿射投影

【数学】正投影和仿射投影

正投影 (Orthographic projection) Weak perspective projection Affine projection 形式1 形式2
阅读更多...
BGP引入实验，华为ensp模拟器

BGP引入实验，华为ensp模拟器

一个小作业题&#xff0c;中间三台路由器bgp 100 分支用rip和ospf&#xff0c;最后如有引入时通过前缀列表精确匹配和路由策略调用&#xff0c;都是一些基本配置&#xff0c;考研学生们的基本功扎不扎实&#xff0c;从最最基础的接口配ip&#xff0c;到igp的路由配置&#xff0…
阅读更多...
独立站和跨境电商平台的一个优缺点对比，哪个更适合你？

独立站和跨境电商平台的一个优缺点对比，哪个更适合你？

不管哪个行业都是一样的&#xff0c;有优点也有缺点&#xff0c;就像人们常说的人无完人一样。然后&#xff0c;我们来说说最近比较受关注的跨境电商独立站和跨境电商平台的一个优缺点对比吧&#xff01; 了解跨境电商独立站 建站&#xff0c;测试模板网站 跨境电商独立站 优点…
阅读更多...
早上好图片漂亮祝福语，祝你事业芝麻节节高，好运连连天天妙！

早上好图片漂亮祝福语，祝你事业芝麻节节高，好运连连天天妙！

1、清晨&#xff0c;我呼吸着新鲜空气&#xff0c;迎面的风捎来了你的气息&#xff0c;不知你现在在哪里&#xff1f;希望在这美丽的早晨时时见到开开心心的你&#xff0c;早安&#xff01; 2、无论岁月如何变幻&#xff0c;不变的是心态&#xff0c;改变的是容颜&#xff0c;…
阅读更多...
阿里云CentOS主机开启ipv6

阿里云CentOS主机开启ipv6

目录 一、云主机开启和使用 ipv6 1、网络和交换机开启 ipv6 2、创建 / 编辑云主机&#xff0c;开启ipv6 3、安全组放行ipv6端口 二、使用 ipv6 地址进行 ssh 连接 三、ipv6 地址绑定域名 一、云主机开启和使用 ipv6 1、网络和交换机开启 ipv6 进入网络、交换机详情页面…
阅读更多...
低代码是“银弹”，还是“毒弹”？

低代码是“银弹”，还是“毒弹”？

目录 1.Pro Code 真的更“香”吗&#xff1f; 门槛高 跨界难 代码编写只是第一步 2.Low Code 银弹论合理吗&#xff1f; Pro Code和Low Code的差异&#xff1a; 3.写在最后 “低代码”接力“中台”燃起了熊熊之火&#xff0c;引发了众多业内人士论战。有人认为低代码是毒瘤&…
阅读更多...
使用FP8加速PyTorch训练

使用FP8加速PyTorch训练

现代的人工智能硬件架构(例如&#xff0c;Nvidia Hopper, Nvidia Ada Lovelace和Habana Gaudi2)中&#xff0c;FP8张量内核能够显著提高每秒浮点运算(FLOPS)&#xff0c;以及为人工智能训练和推理工作负载提供内存优化和节能的机会。 在这篇文章中&#xff0c;我们将介绍如何修…
阅读更多...
DBeaver 23.2.4发布

DBeaver 23.2.4发布

导读DBeaver 23.2.4发布,修复和添加了一些新功能。 SQL 编辑器 为更新语句添加了代码自动补全功能修复了智能补全和替换带引号表达式的问题删除了日志中首次打开 SQL 编辑器时出现的多余错误 数据库导航器 添加了过滤对象可视化功能修复了脚本文件夹打开问题 数据传输 正确…
阅读更多...
消除“数据烟囱”，瓴羊港如何打破壁垒将多数据融通成大数据？

消除“数据烟囱”，瓴羊港如何打破壁垒将多数据融通成大数据？

作为数字经济时代的“新石油”&#xff0c;数据已成为重要的生产要素。阿里巴巴副总裁、瓴羊CEO朋新宇认为&#xff0c;目前正处在数据流通变革的时代&#xff0c;其中最核心的问题是如何破解数实融合发展的堵点。数据流通中最重要的原则是&#xff0c;不流通无价值&#xff0c…
阅读更多...
echarts 实现同一组legend控制两个饼图示例

echarts 实现同一组legend控制两个饼图示例

实现同一组legend控制两个饼图示例&#xff1a; 该示例有如下几个特点&#xff1a; ①饼图不同值实现分割 ②实现tooltip自定义样式&#xff08;echarts 实现tooltip提示框样式自定义-CSDN博客&#xff09; ③自定义label内容 ④不同值颜色渐变 代码如下&#xff1a; this.o…
阅读更多...
html实现图片裁剪处理(附源码)

html实现图片裁剪处理(附源码)

文章目录 1.设计来源1.1 主界面1.2 裁剪界面 2.效果和源码2.1 动态效果2.2 源代码 源码下载 作者&#xff1a;xcLeigh 文章地址&#xff1a;https://blog.csdn.net/weixin_43151418/article/details/134455169 html实现图片裁剪处理(附源码)&#xff0c;支持图片放大缩小&#…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023