树状数组（Binary Index Tree, BIT），是一种一般用来处理单点修改和区间求和操作类型的题目的数据结构，时间复杂度为O(log n)。

        对于普通数组来说，单点修改的时间复杂度是 O(1)，但区间求和的时间复杂度是 O(n) 。如果使用前缀和数组呢？区间求和的时间复杂度降低为O(1)，但是单点修改又会变为O(n) 。那么，我们能不能找到一种数组，中和两者的时间复杂度都不那么高？

        树状数组就是这么一种结构，它通过二进制来划分区间，例如我们要求出前13项的和，13的二进制表示为(1101)，接着分别查询((0000), (1000)]，((1000), (1100)]，和((1100), (1101)]的和并相加。

        上述区间的划分规则是将13不断减去最低位的1来划分的，这里就需要用的之前学过的lowbit()，acwing基础课——位运算_acwing位运算_我的鱼干呢w的博客-CSDN博客可从这里学习lowbit()的用法和实现。

        树状数组的大致结构如下：

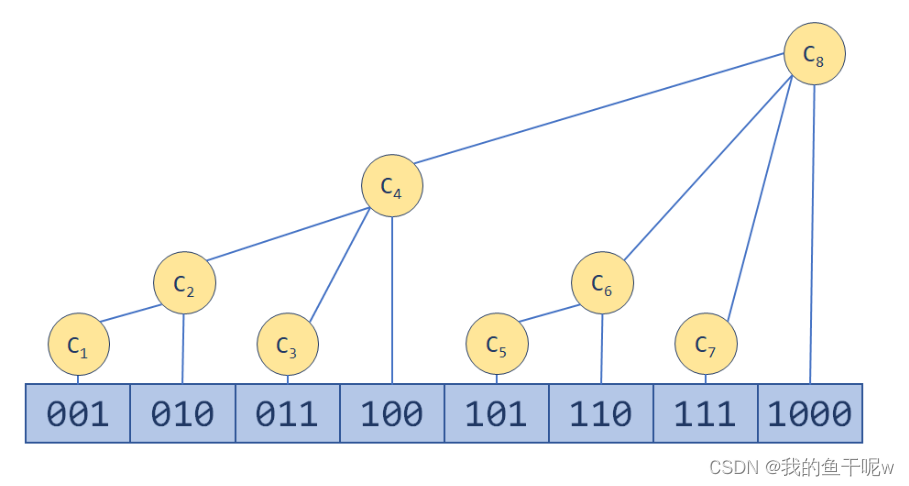
        通过树状数组，我们需要更新的区间至多不会超过log~2~N，这样我们就能以O(log n)的时间复杂度完成单点修改和区间查询。下面给出树状数组的实现：

//单点修改
void modify(int k, int x)
{
    for(int i = k; i <= n; i += lowbit(i)) tr[i] += x;
}

//统计前x项的和
int count(int x)
{
    int res = 0;
    for(int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

//区间求和
int query(int a, int b)
{
    return count(b) - count(a - 1);
}

来到例题练练手吧！

241. 楼兰图腾 - AcWing题库

在完成了分配任务之后，西部 314 来到了楼兰古城的西部。

相传很久以前这片土地上(比楼兰古城还早)生活着两个部落，一个部落崇拜尖刀(V)，一个部落崇拜铁锹(∧)，他们分别用 V 和 ∧ 的形状来代表各自部落的图腾。

西部 314 在楼兰古城的下面发现了一幅巨大的壁画，壁画上被标记出了 n 个点，经测量发现这 n 个点的水平位置和竖直位置是两两不同的。

西部 314 认为这幅壁画所包含的信息与这 n 个点的相对位置有关，因此不妨设坐标分别为 (1,y1),(2,y2),…,(n,yn)其中 y1∼yn 是 1 到 n 的一个排列。

西部 314 打算研究这幅壁画中包含着多少个图腾。

如果三个点 (i,yi),(j,yj),(k,yk) 满足 1≤i<j<k≤n 且 yi>yj,yj<yk，则称这三个点构成 V 图腾;

如果三个点 (i,yi),(j,yj),(k,yk) 满足 1≤i<j<k≤n 且 yi<yj,yj>y，则称这三个点构成 ∧ 图腾;

西部 314 想知道，这 n 个点中两个部落图腾的数目。

因此，你需要编写一个程序来求出 V 的个数和 ∧ 的个数。

输入格式

第一行一个数 n。

第二行是 n 个数，分别代表 y1，y2,…,yn。

输出格式

两个数，中间用空格隔开，依次为 V 的个数和 ∧ 的个数。

数据范围

对于所有数据，n≤200000，且输出答案不会超过 int64。
y1∼yn 是 1 到 n 的一个排列。

输入样例：

5
1 5 3 2 4

输出样例：

3 4

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 200010;

int n;
int a[N];
int tr[N];
int Greator[N], Lower[N];

int lowbit(int x)
{
    return x & -x;
}

void add(int k, int x)
{
    for(int i = k; i <= n; i += lowbit(i)) tr[i] += x;
}

int sum(int x)
{
    int res = 0;
    for(int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i ++ ) cin >> a[i];
    
    for(int i = 1; i <= n; i ++ )
    {
        int u = a[i];
        Greator[i] = sum(n) - sum(u);
        Lower[i] = sum(u - 1);
        add(u, 1);
    }
    
    memset(tr, 0, sizeof tr);
    
    LL res1 = 0, res2 = 0;
    for(int i = n; i; i -- )
    {
        int u = a[i];
        res1 += (LL)Greator[i] * (sum(n) - sum(u));
        res2 += (LL)Lower[i] * sum(u - 1);
        add(u, 1);
    }
    
    cout << res1 << " " << res2;
    
    return 0;
}