百钱买百鸡的问题算是一套非常经典的不定方程的问题，题目很简单：公鸡5文钱一只，母鸡3文钱一只，小鸡3只一文钱，用 100 文钱买一百只鸡,其中公鸡，母鸡，小鸡都必须要有，问公鸡，母鸡，小鸡要买多少只刚好凑足 100 文钱。
分析：估计现在小学生都能手工推算这套题，只不过我们用计算机来推算，我们可以设公鸡为 x，母鸡为 y，小鸡为 z，那么我们
可以得出如下的不定方程，

x+y+z=100,
5x+3y+z/3=100，

下面再看看x，y，z的取值范围。由于只有100文钱，则5x<100 => 0<x<20, 同理 0<y<33,那么z=100-x-y，好，我们已经分析清楚了，下面就可以编码了。

 class Program
 {
     static void Main(string[] args)
     {
         //公鸡的上线
         for (int x = 1; x < 20; x++)
         {
             //母鸡的上线
             for (int y = 1; y < 33; y++)
             {
                 //剩余小鸡
                 var z = 100 - x - y;

                 if ((z % 3 == 0) && (x * 5 + y * 3 + z / 3 == 100))
                 {
                     Console.WriteLine("公鸡:{0}只，母鸡:{1}只,小鸡:{2}只", x, y, z);
                 }
             }
         }
         Console.Read();
     }
 }

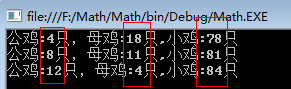
结果出来了，确实这道题非常简单，我们要知道目前的时间复杂度是 O(N2),实际应用中这个复杂度是不能让你接受的，最多最多能让人接受的是 O(N)。所以说我们必须要优化一下，从结果中我们可以发现这样的一个规律：公鸡是 4 的倍数,母鸡是 7 的递减率，小鸡是 3 的递增率，规律哪里来，肯定需要我们推算一下这个不定方程。
x+y+z=100 ①
5x+3y+z/3=100 ②
令 ②x3-① 可得
7x+4y=100
=>y=25-(7/4)x ③
又因为 0<y<100 的自然数，则可令
x=4k ④
将 ④ 代入 ③ 可得
=> y=25-7k ⑤
将 ④⑤ 代入 ① 可知
=> z=75+3k ⑥
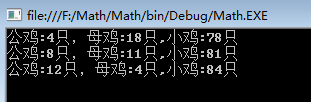
要保证 0<x，y，z<100 的话，k 的取值范围只能是 1,2,3，下面我们继续上代码。

 class Program
 {
     static void Main(string[] args)
     {
         int x, y, z;

         for (int k = 1; k <= 3; k++)
         {
             x = 4 * k;
             y = 25 - 7 * k;
             z = 75 + 3 * k;

             Console.WriteLine("公鸡:{0}只，母鸡:{1}只,小鸡:{2}只", x, y, z);
         }

         Console.Read();
     }
 }