一、说明
关于复杂问题,始终是计算机科学挡在路前的一块巨石。所谓一个问题有解,但需要秒完成,这相当于说,此类问题无解。还有一类问题是说不清楚到底有没有一个具体解法,该解法能在多项式时间复杂函数上完成,也就是说:目前还没找到好方法的问题。以上归于NP类问题,本文专门讨论NP类问题的前因后果,以增加读者的见识。
二、基本概念
2.1 对问题分类
在继续之前,我们需要根据相应搜索空间中的对象类型对优化问题进行进一步的区分。如果搜索空间 S 由连续变量(即实数)定义,那么我们就有一个数值优化问题。如果 S 由离散变量(例如布尔值或整数)定义,那么我们就有一个组合优化问题。为组合优化问题定义了进一步讨论的各种问题硬度概念。请注意,离散搜索空间始终是有限的,或者在最坏的情况下,是可数的无限。
2.2 围绕P类问题的几个概念
我们并不试图提供计算复杂性的完整概述,因为这在许多书籍中都有很好的介绍。相反,我们简要概述了一些重要概念,它们对解决问题的影响,以及一些非常常见的误解。此外,我们没有以数学上的严谨性来对待这个主题。因此,我们不会给出基本概念的精确定义,如算法、问题大小或运行时,而是以直观的方式使用这些术语,并在必要时通过示例解释它们的含义。
计算复杂性的第一个关键概念是问题大小,它基于手头问题的维度(即变量的数量)和问题变量的不同值的数量。对于前面讨论的例子,要访问的城市数量,或者要放在板上的皇后数量可能是表明问题大小的明智措施。
第二个概念涉及算法,而不是问题。算法的运行时间是终止所需的基本步骤或操作数。计算复杂性背后的一般直觉(尽管并不总是正确的)是更大的问题需要更多的时间来解决。问题硬度最广为人知的定义是将问题的大小与求解问题的算法的(最坏情况)运行时间联系起来。这种关系由一个公式表示,该公式将最坏情况运行时间的上限指定为问题大小的函数。简单地说,这个公式可以是多项式(被认为表示相对较短的运行时间)或超多项式,例如指数(表示较长的运行时间)。
第三个概念是问题减少,即我们可以通过合适的映射将一个问题转化为另一个问题。请注意,转换可能是不可逆的。尽管这种转换或减少问题的想法有点复杂,但现实世界中的给定问题通常可以以不同但等效的方式形式化,这并不完全陌生。关于问题硬度的常用概念现在可以表述如下。
如果存在一种可以在多项式时间内解决问题的算法,则称问题属于 P 类。也就是说,如果存在一种算法,其问题大小 n 的最坏情况运行时间小于某些多项式公式 F 的 F(n)。通俗地说,集合 P 包含可以轻松解决的问题,例如最小生成树问题。简而言之P问题就是可以搞定的问题。
三、NP问题专论
3.1 NP完全问题
任何一类尚未找到有效解决算法的计算问题。许多重要的计算机科学问题都属于此类,例如旅行商问题、可满足性问题和图覆盖问题。
所谓的容易,或者易于处理,问题可以通过在多项式时间内运行的计算机算法来解决;即对于一个问题大小n,找到解决方案所需的时间或步骤数是n的多项式函数。解决难题的算法,或者另一方面,棘手的问题需要时间问题大小n的指数函数。多项式时间算法被认为是有效的,而指数时间算法被认为是低效的,因为随着问题规模的增加,后者的执行时间增长得更快。
一个问题称为 NP (非确定性多项式)如果它的解可以是在多项式时间内猜测和验证;不确定性意味着不遵循特定规则进行猜测。如果一个问题是 NP 问题,并且所有其他 NP 问题都可以多项式时间简化为该问题,则该问题是 NP 完全问题。
因此,为任何 NP 完全问题找到一个有效的算法意味着可以为所有此类问题找到一个有效的算法,因为属于此类的任何问题都可以重新转换为该类的任何其他成员。目前尚不清楚是否会找到解决 NP 完全问题的多项式时间算法,并且确定这些问题是否易于处理仍然是理论计算机科学 中最重要的问题之一。当必须求解NP完全问题时,一种方法是使用多项式算法来近似解;由此获得的答案不一定是最优的,但会相当接近。
3.2 NP等效性选择
如果一个问题可以通过某种算法(没有关于其运行时的声明)来解决,并且任何解决方案都可以在多项式时间内通过其他算法进行验证,则该问题被称为属于 NP 类。请注意,P 是 NP 的子集,因为多项式求解器也可用于验证多项式时间内的解。NP 问题的一个例子是子集总和问题:给定一组整数,该集合中是否有一个或多个元素的总和为零?显然,对于给定的数字集,对这个问题给出否定的答案需要检查所有可能的子集。
不幸的是,在集合的大小上,可能的子集的数量超过了多项式。但是,验证解决方案是否有效仅涉及对发现的子集的内容求和。如果一个问题属于 NP 类,则称它属于 NP 类,并且 NP 中的任何其他问题都可以通过在多项式时间内运行的算法简化为这个问题。在实践中,这些都是不断出现的难题。在互联网上可以很容易地找到几个著名的NP完备问题的例子——我们不会试图总结,只是说计算机科学中绝大多数有趣的问题都是NP完备的。
3.3 复杂问题和NP-hard
最后,如果一个问题至少与 NP-complete 中的任何问题一样难(因此 NP-complete 中的所有问题都可以简化为 NP-hard 中的一个问题),但解不一定在多项式时间内得到验证,则称该问题属于 NP-hard 类。一个这样的例子是停止问题。在多项式时间内无法验证解的问题的存在证明了 P 类与 NP-hard 类不同。目前尚不清楚的是,P 和 NP 这两个类实际上是否相同。如果是这样的话,那么对计算机科学和数学的影响将是巨大的,因为众所周知,对于以前认为困难的问题,必须存在快速算法。因此,P = NP 是否是复杂性理论的一大挑战,并且对于任何证明 P = NP 或 P != NP 的证明,都会提供一百万美元的奖励。
请注意,虽然后者是复杂数学的主题,但前者可以通过为任何NP完全问题创建一个快速算法来证明,例如,一个用于旅行推销员问题的算法,其最坏情况下的运行时间与城市数量呈多项式比例。图 1.4 显示了根据 P 和 NP 的相等性的问题硬度等级。如果 P = NP,则集合 P = NP = NP-complete,但它们仍然是 NP-hard 的子集。
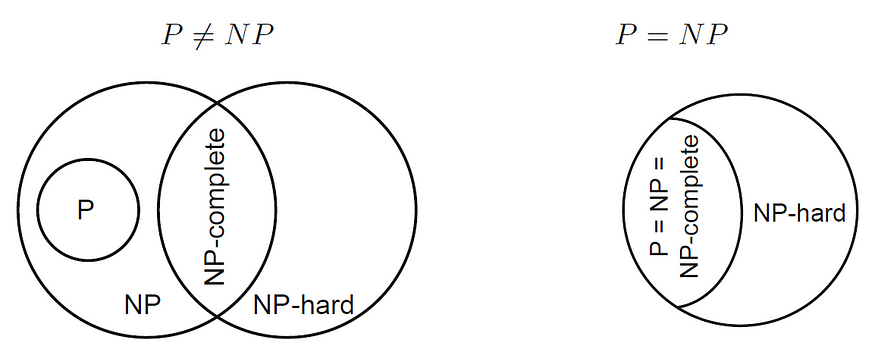
图 1.4.问题硬度的等级取决于 P 和 NP 的相等性
虽然这听起来很理论化,但它对解决问题有一些非常重要的影响。如果一个问题是NP完备的,那么尽管我们可能能够在多项式时间内解决特定实例,但我们不能说我们能够在所有可能的实例中都这样做。因此,如果我们希望将解决问题的方法应用于这些问题,我们目前必须要么接受我们可能只能解决非常小(或其他简单)的实例,要么放弃提供精确解决方案的想法,并依靠近似或元启发式来创建足够好的解决方案。这与已知的 P 中的问题形成鲜明对比。尽管这些问题的可能解决方案的数量可能会呈指数级增长,但存在一些算法可以找到解决方案,并且其运行时间与实例的大小呈多项式关系。
总而言之,有大量的实际问题,经过检查,这些问题被证明是已知属于NP完备类的抽象问题的变体。尽管此类问题的某些实例可能很容易,但大多数计算机科学家认为,对于此类问题不存在多项式时间算法,当然还没有发现。因此,如果我们希望能够为此类问题的任何实例创建可接受的解决方案,我们必须转向使用近似和元启发式方法,并放弃绝对找到可能最适合该实例的解决方案的想法。